Лабораторная работа № 5

ИЗУЧЕНИЕ ОСНОВНЫХ ЗАКОНОМЕРНОСТЕЙ

ГИДРОДИНАМИКИ И РЕОЛОГИИ

1.Теоретическая часть

§1. Линии и трубки тока. Уравнение неразрывности струи

Гидродинамика – раздел гидроаэромеханики, в котором изучается движение несжимаемых жидкостей и их взаимодействие с твердыми телами.

В гидродинамике различают понятия идеальной и реальной жидкостей.

Идеальной называют воображаемую жидкость, лишенную вязкости и теплопроводности.

Для описания движения жидкости используют понятия «линия тока» и «трубка тока». При установившемся течении все частицы жидкости движутся по определенным траекториям с определенными скоростями.

Линия тока – это линия, в каждой точке которой вектор скорости частицы направлен по касательной (рис.1.).

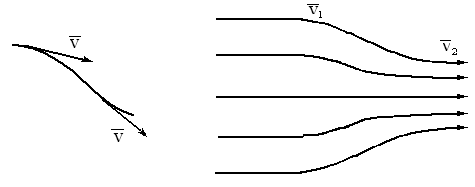
Рис.1 Рис.2

Понятие линии тока позволяет изобразить поток жидкости графически. Условились проводить линии тока так, чтобы густота их была пропорциональна величине скорости в данном месте. Там, где линии проведены гуще, скорость течения больше и наоборот (рис.2).

В общем случае величина и направление вектора в каждой точке пространства могут изменяться со временем, поэтому и картина линий тока будет меняться.

Возможно течение, при котором любая частица жидкости проходит данную точку пространства с одной и той же скоростью. Течение принимает стационарный характер.

Стационарным называют такое течение, при котором в данной точке вектор скорости не изменяется с течением времени.

Трубка тока – это объем жидкости, ограниченный линиями тока (рис.3).

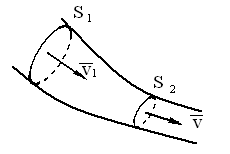
S₁ и S₂ – два произвольных сечения трубки тока;

и _– скорости течения жидкости в этих сечениях.

Рассмотрим сечение S трубки тока, перпендикулярное скорости (рис.4).

Рис. 4

За время t через сечение S пройдут все частицы, расстояние которых от S в начальный момент времени не превышает расстояние l = vt. Поэтому за время t через сечение S пройдет объем жидкости

V = S (1)

А за единицу времени объем

Q = (1)

Теорема о неразрывности струи: при стационарном течении идеальной жидкости произведение площади поперечного сечения S трубки тока на скорость сечения жидкости v есть величина постоянная для любого сечения трубки тока, т.е.

S  v =const

Для доказательства возьмем трубку тока настолько тонкую, что в каждом сечении скорость можно считать постоянной (рис.5.) Жидкость абсолютно несжимаема, т.е. ее плотность во всем объеме жидкости одинакова и неизменна. Тогда количество жидкости между сечениями S и S будет оставаться постоянным, а

Рис. 5

это возможно только при условии, что объем

жидкости, протекающей через сечение S и S за время одинаковы, т.е.v=v или, учитывая (1), можно записать

Sv= Sv(2)

Приведенные рассуждения справедливы для любой пары сечений трубки тока, поэтому величина Sv для любого сечения трубки тока должна быть одна и та же.

Условие неразрывности струи применимо и к реальным жидкостям и газам, если их сжимаемостью можно пренебречь.

На рис.4 буквами ри робозначены статические давления (давления напора) по обе стороны выделенного объема жидкостиV = Sl.

Чтобы скорость течения была направлена, как показано на рисунке, необходимо выполнение условия р>р.

Тогда работа А по перемещению выбранного нами объема жидкости будет совершаться за счет разности сил давления F- F= рS - рS

А=

Учитывая, что , можно записать

. (3)