savastenko / 11. Основные определения теории графов (включая ориентированные графы)

11. Основные определения теории графов (включая ориентированные графы).

Граф описывается перечислением множества вершин и рёбер. Объекты представляются как вершины графа, а связи — как рёбра.

Граф называется связным, если для любых вершин u,v есть путь из u в v.

При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

Х = {х_i}, i = 1, 2, 3, 4 – множество вершин; А = {a_i }, i = 1, 2, ..., 6 – множество дуг, причем А = {(х₁, х₂), (х₄, х₂), (х₂, х₄ ), (х₂, х₃), (х₃, х₃), (х₄ , х₁)}.

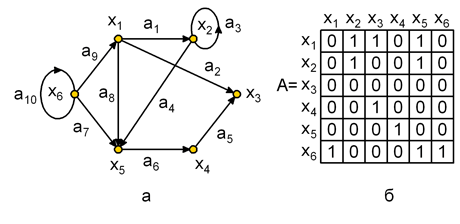
Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины.

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i,

Ориентированный граф (кратко орграф) — граф, вершины которого соединены направленными ребрами.

Маршрутом в орграфе называют чередующуюся последовательность вершин и рёбер, вида v₀{v₀,v₁}v₁{v₁,v₂}v₂...v_n (вершины могут повторяться). Длина маршрута — количество рёбер в нем.

Путь есть маршрут в орграфе без повторяющихся дуг, простой путь — без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой. Контур если замкнутый путь.

Орграф сильно связный, или просто сильный если все его вершины взаимно достижимы; односторонне связный, или просто односторонний если для любых двух вершин, по крайней мере одна достижима из другой; слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;

Орграфы широко применяются в программировании как способ описания систем со сложными связями.