4.3. Генераторы псевдослучайных последовательностей

Отметим, что для создания РРСП используется три типа генераторов: табличные, физические генераторы и генераторы ПСП.

Примером табличного генератора может служить опубликованная в 1955 году компанией Rand Corporation таблица объемом 106 случайных цифр.

Физические генераторы получили широкое распространение после создания микропроцессоров, имеющие невысокую стоимость при условии достаточной производительности. На рис. 4.1 представлен физический генератор случайных данных ORB, реализованный компанией APA Consulting на микроконтроллере семейства PIC12C67X (8-ми контактный корпус SOIC размером 5.38.1мм).

Рис. 4.1. Генератор случайных чисел ORB

В основу работы данного генератора положен принцип измерения напряжения на конденсаторе, который заряжается и разряжается в соответствии с некоторым потоком бит.

Первые два типа генераторов наряду с хорошими статистическими свойствами имеют ряд недостатков, к главным из которых можно отнести сложность технической реализации, невысокое быстродействие и высокую стоимость.

В силу названных причин при построении программных и программно-аппаратных средств криптографической защиты информации широкое распространение получили генераторы ПСП

Наиболее простым программным датчиком псевдослучайных чисел является линейный конгруэнтный генератор (ЛКГ), который описывается рекуррентным уравнением вида , где– случайное начальное значение,– множитель,– приращение,– модуль.

Период выходной последовательности такого генератора не превышает , максимальное значение достигается при правильном выборе параметров, а именно, когда:

– числа ивзаимно просты: НОД;

– кратно любому простому , делящему;

– кратно 4, если кратно 4.

В [10] приведен список констант для ЛКГ, обеспечивающих максимальный период последовательности и, что не менее важно, соответствующие последовательности проходят статистические тесты.

Для реализации ЛКГ на персональных компьютерах с учетом их разрядной сетки нередко используется модуль . При этом наиболее качественные статистические свойства ПСП достигаются для константы.

По сравнению с другими видами генераторов ПСП данный вид обеспечивает высокую производительность за счет малого числа операций для создания одного псевдослучайного бита.

Недостатком ЛКГ в плане их использования для создания поточных шифров является предсказуемость выходных последовательностей.

Эффективные атаки на ЛКГ были предложены Joan Boyar.

Ей принадлежат методы атак на квадратичные и кубические генераторы: и.

Другие исследователи обобщили результаты работ Boyar на случай общего полиномиального конгруэнтного генератора. Stern и Boyar показали, как взломать ЛКГ, даже если известна не вся последовательность.

Wishmann и Hill, а позже Pierre L’Ecuger изучили комбинации ЛКГ. Усложнения не являются более стойкими криптографически, но имеют большие периоды и лучше ведут себя на некоторых критериях случайности.

Регистры сдвига с линейной обратной связью (Linear Feedback Shift Registers – LFSR) включают собственно регистр сдвига и схему вычисления функции обратной связи (tap sequence) – см. рис. 4.2.

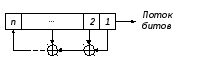
Рис. 4.2 Регистр сдвига с линейной обратной связью (LFSR)

На схеме содержимое регистра – последовательность битов – сдвигается с приходом тактового импульса (clock pulse) на один разряд вправо. Бит самого младшего разряда считается выходом LFSR в данном такте работы. Значение самого старшего разряда при этом является результатом сложения по модулю 2 (функция XOR) разрядов (точек съема) обратной связи. Генерируемая последовательность называется линейной рекуррентой.

Теоретически, -битный LFSR может сгенерировать псевдослучайную последовательность с периодомбит. Такие LFSR называются регистрами максимального периода [1].

Для этого регистр сдвига должен побывать во всех ненулевых внутренних состояниях.

Одна и та же рекуррента может быть сгенерирована регистрами разной длины. Предположим, что среди подобных регистров наш -битный LFSR обладает минимальной длиной.

Функции обратной связи регистра можно сопоставить полином степени не вышес коэффициентами из поля вычетов по модулю два, состоящий из одночленов вида, где- множество номеров точек съема обратной связи.

Полином называетсяминимальным полиномом соответствующей рекуррентной последовательности.

Для каждой конечной (или периодической) последовательности можно указать LFSR, который, при некотором начальном заполнении, порождает эту последовательность.

Среди всех таких регистров, существует регистр минимальной длины .

Величина называетсялинейной сложностью последовательности .

Напомним, что полином называется неприводимым, если он не может быть выражен как произведение двух полиномов меньшей степени, отличных констант.

Примитивный полином степени над полем вычетов по модулю два – это неприводимый полином, который делит, но не делитдля любых:.

Теорема. Для того, чтобы последовательность, порожденная LFSR имела максимальный период, необходимо и достаточно, чтобы ее минимальный полином, был примитивным полиномом по модулю 2.

Список практически применимых примитивных полиномов приведен в [1,7]. Например, примитивным полиномом является .

Набор показателей означает, что, взяв регистр сдвига длины 32 и генерируя бит обратной связи путем сложения 7-го, 5-го, 3-го, 2-го и 1-го бита по модулю 2, мы получим LFSR максимальной длины (ссостояниями).

Приведем программу на языке С для последовательности генерируемой данным LFSR:

Int LFSR() {

Static unsigned long ShiftRegister=1; //любое ненулевое начальное заполнение

ShiftRegister = (((( ShiftRegister>>31)

^( ShiftRegister>>6)

^( ShiftRegister>>4)

^( ShiftRegister>>2)

^( ShiftRegister>>1)

^( ShiftRegister))

&0x00000001)

<<31

| ShiftRegister>>1);

return ShiftRegister & 0x00000001;

}

Заметим, если – примитивный полином, то– также примитивный. Кроме того, если полиномпримитивный, то– примитивный. Если полиномпримитивный, то– примитивный и т.п.

Примитивные трехчлены особенно удобны, т.к. складываются только 2 бита регистра сдвига, но при этом они и более уязвимы к атакам.

Вообще говоря, LFSR – удобны для технической реализации, но с точки зрения криптографической стойкости, обладают слабостями.

Последовательные биты линейной рекурренты линейно зависимы, что делает их бесполезными для шифрования.

Достаточно последовательных битов рекурренты, чтобы определить множество номеров точек съема обратной связи.

Большие случайные числа, сгенерированные из последовательных битов LFSR, сильно коррелированны. Тем не менее, LFSR достаточно часто используются в качестве элементов более сложных алгоритмов формирования шифрующей ключевой последовательности.

Существует еще ряд генераторов ПСП (в т.ч. генераторы Галуа), которые по ряду причин не нашли широкого применения в криптографических системах. Наиболее эффективные решения были получены на основе составных генераторов [11].

Идея построения составного генератора базируется на том факте, что комбинация двух и более простых генераторов ПСП, в случае правильного выбора объединяющей функции (в т.ч. сложение по модулям, и др.), дает генератор с улучшенными свойствами случайности, и, как следствие, с повышенной криптографической стойкостью.

В случае создания криптографически стойкого генератора ПСП легко решается вопрос создания потоковых шифров. Выход таких ПСП неотличим (точнее, должен быть неотличим) от РРСП. Два генератора всегда могут быть синхронно запущены из одного вектора начального состояния, который намного короче передаваемого сообщения, что выгодно отличает эту схему от шифра Вернама.

Известно 4 подхода к конструированию соответствующих генераторов:

1) системно-теоретический подход;

2) сложностно-теоретический подход;

3) информационно-теоретический подход;

4) рандомизированный подход.

Эти подходы различаются в своих предположениях о возможностях криптоаналитика, определении криптографического успеха и понятия надежности.

В случае системно-теоретического подхода криптограф создает генератор ключевого потока, который обладает поддающимися проверке свойствами, включая длину периода выходной последовательности, статистическое распределение потока бит, линейную сложность преобразования и т.д.

С учетом известных методов криптоанализа криптограф оптимизирует генератор против этих атак.

На основе такого подхода Рюппелем сформулирован следующий набор критериев для потоковых шифров.

1.Большой период выходной последовательности, отсутствие повторений.

2. Высокая линейная сложность, как характеристика нашего генератора через регистр LFSR минимальной длины, который может сгенерировать такой же выход.

3. Неотличимость от РРСП по статистическим критериям.

4. Перемешивание: любой бит ключевого потока должен быть сложным преобразованием всех или большинства бит начального состояния (ключа).

5. Рассеивание: избыточность во всех подструктурах алгоритма работы генератора должна рассеиваться.

6. Критерии нелинейности преобразований: в соответствии с некоторой метрикой расстояние до линейных функций должно быть достаточно большим; требуется лавинообразное распространения ошибок в случае изменения одного бита аргумента и др.

Практика подтверждает целесообразность применения указанных критериев не только для анализа и оценки потоковых шифров, созданных в рамках системно-теоретического подхода, но и для любых потоковых и блочных шифров.

Основная проблема подобных криптосистем заключается в том, что для них трудно доказать какие-либо факты об их криптостойкости, так как для всех этих критериев не была доказана их необходимость или достаточность.

Потоковый шифр может удовлетворять всем этим принципам и все-таки оказаться нестойким, т.к. стойкость по отношению к заданному набору криптоаналитических атак ничего не гарантирует.

Примером удачного построения составного генератора с точки зрения повышения линейной сложности является каскад Голмана (рис. 4.3). Каскад Голмана включает несколько регистров сдвига LFSR. Первый регистр движется равномерно с шагом 1. Сдвиг каждого последующего регистра управляется предыдущим так, что изменение состояния последующего регистра в такте происходит, если в тактес предыдущего регистра снимается 1. Иначе, состояние последующего регистра не изменяется.

Если все LFSR – длины , то линейная сложность системы срегистрами равна.

Рис. 4.3. Каскад Голлмана

Типичным примером комбинирования регистров сдвига является схема чередующегося «старт-стоп» генератора (Alternating Stop-and-Go Generator).

У этого генератора большой период и большая линейная сложность.

В «старт-стоп» генераторе (рис. 4.4) используется три линейных регистра сдвига различной длины. LFSR-2 меняет состояние, если выход LFSR-1 равен 1; LFSR-3 меняет состояние в противном случае. Результат генератора есть сложение по модулю 2 выходов регистров LFSR-2, LFSR-3.

Рис. 4.4. Чередующийся старт-стопный генератор

Применяя сложностно-теоретический подход, криптограф пытается доказать стойкость генератора, используя теорию сложности.

Основу решений при этом подходе составляют генераторы, базирующиеся на понятии однонаправленной функции.

Значение однонаправленной функции легко вычислимо, но почти для всех значений практически невозможно определить соответствующее значение. Иначе, если– вычислительная сложность получения, а– вычислительная сложность нахождения, то.

По общему мнению, одним из кандидатов на однонаправленную функцию может быть показательная функция в некотором конечном поле , где.

Нетрудно видеть, что возведение в степень можно ускорить за счет свойств ассоциативности. Например, , что позволяет вычислить степень за четыре шага, вместо восьми.

Обратная операция – задача нахождения показателя степени по значению степенной функции (дискретный логарифм), в общем случае, пока не может быть решена лучше, чем с помощью оптимизированных методов перебора.

При соответственно выбранной характеристике и степени расширения поляэта задача при современном развитии компьютерной техники вычислительно неразрешима.

Примером генератора на основе однонаправленной функции может служить генератор на основе алгоритма RSA с параметрами вида. Здесь, где– секретные большие, неравные простые числа,– показатель степенной функции, НОД,.

Результат работы одного такта генератора – младший бит . Стойкость этого генератора не ниже стойкости RSA. Еслидостаточно большое, то генератор обеспечивает практическую стойкость.

BBS – другой пример генератора, построенного на сложностном подходе (предложен Blum, Blum и Shub).

Это один из простых и эффективных алгоритмов. Математическая теория этого генератора – квадратичные вычеты по составному модулю .

Параметры генератора: секретные большие, неравные простые числа, , такие, что,; число;– случайный секретный вычет помодулю.

Первым шагом вычисляется начальное состояние .

В основном цикле елемент ПСП з номером равен, т.е-ым псевдослучайным числом является младший бит числа .

Заметим, что алгоритм можно использовать для шифрования файлов с произвольным доступом, если, кроме , ввести секретный параметр, поскольку тогдаможна вычислять через, потому, что, где.

Это свойство позволяет использовать BBS-генератор для работы с файлами произвольного доступа (random-access).

Число можно распространять свободно, для того чтобы каждый абонент сети смог самостоятельно сгенерировать необходимые биты. При этом если криптоаналитик не сможет разложить на простые множители число, он не сможет предсказать следующий бит, даже в вероятностном смысле, например, «с вероятностью 51% следующий бит равен 1».

Отметим, что подобные генераторы очень медленные, для их практической реализации необходимы специальные процессоры.

Следующие два подхода, информационно-теоретический и рандомизированный, не нашли широкого практического применения.

С точки зрения информационно-теоретического похода самым лучшим средством в борьбе с криптоаналитиком, имеющим бесконечные вычислительные ресурсы и время, является одноразовая лента или одноразовый блокнот.

В случае рандомизированного подхода задача заключается в том, чтобы увеличить число бит, с которыми необходимо работать криптоаналитику (не увеличивая при этом ключ). Этого можно достичь путем использования больших случайных общедоступных строк.

Ключ будет обозначать, какие части (или биты) этих строк необходимо использовать для зашифрования и расшифрования. Тогда криптоаналитику придется использовать метод тотального перебора вариантов (грубой силы) на случайных строках.

Стойкость этого метода может быть выражена в терминах среднего числа бит, которые придется изучить криптоаналитику, прежде чем шансы определить ключ станут выше простого угадывания.

Ueli Maurer описал такую схему. Вероятность вскрытия такой криптосистемы зависит от объема памяти, доступного криптоаналитику (но не зависит от его вычислительных ресурсов).

Чтобы эта схема приобрела практический вид, требуется около 100 битовых последовательностей по битов каждая. Оцифровка поверхности Луны – один из способов получения такого количества бит.

В заключение отметим, что для построения генератора ПСП необходимо получить несколько случайных битов. Наиболее простой способ: использовать наименьший значимый бит таймера компьютера.

С помощью такого способа нельзя получать много бит, т.к. каждый вызов процедуры генерации бита может занимать четное число шагов таймера, что обязательно скажется на свойствах последовательности.

Самый лучший способ получить случайное число – это обратиться к естественной случайности реального мира – шумы в результате переходных процессов в полупроводниковых диодах, тепловые шумы высокомных резисторов, радиоактивный распад и т.д.

В принципе, элемент случайности есть и в компьютерах:

– время дня;

– загруженность процессора;

– время прибытия сетевых пакетов и т.п.

Проблема не в том, чтобы найти источники случайности, но в том, чтобы сохранить случайность при измерениях.

Например, это можно делать так: найдем событие, случающееся регулярно, но случайно (шум превышает некоторый порог).

Измерим время между первым событием и вторым, затем – времямежду вторым событием и третьим.

Если , то полагаем выход генератора равным 1; если, то выход равен 0. При необходимости, процесс продолжим далее.

Существенной проблемой систем генерации случайных данных является наличие отклонений и корреляций в сгенерированной последовательности. Сами процессы могут быть случайными, но проблемы могут возникнуть в процессе измерений. Как с этим бороться?

Пусть вероятность появления нуля смещена на , т.е. может быть записана как.

Сложение по двух одинаково распределенных независимых битов даст:. При сложении четырех битов получим:. Процесс сходится к равновероятному распределению битов.

Другой подход. Пусть распределение единиц и нулей в последовательности есть величины исоответственно.

Преобразуем последовательные пары битов:

– если это одинаковые биты, то отбросим их и рассмотрим следующую пару;

– если биты различны, то в качестве выходного значения возьмем первый бит.

Данный метод позволяет решить проблему смещения, сохранив свойства случайности источника (с некоторой потерей в объеме данных).

Потенциальная проблема обоих методов в том, что при наличии корреляции между соседними битами, данные методы увеличивают смещение. Один из способов избежать этого – использовать различные источники случайных чисел и суммировать биты подписанных друг под другом последовательностей по вертикали.

Факт наличия смещения у генератора случайных чисел, вообще говоря, не всегда означает его непригодность.

Например, допустим, что для генерации 112-битного ключа для алгоритма «тройной» DES (Triple DES, см. далее) используется генератор со смещением к нулю: ,(энтропия0.99277 на один бит ключа по сравнению с 1 для идеального генератора).

В этом случае нарушитель может оптимизировать процедуру тотального перебора ключей за счет поиска ключа начиная с наиболее вероятного значения и заканчивая наименее вероятным. Вследствие наличия смещения, можно ожидать нахождения ключа в среднем запопыток. Если бы смещения не было, то потребовалось быпопыток.