Метод диаграмм Вейча
Диаграмма Вейча – это специального вида таблица, используемая для задания логических функций и позволяющая упростить процесс поиска минимальных форм.
Для логических функций, зависящих от n переменных, диаграмма Вейча представляет собой прямоугольник, разделенный на 2n клеток. Каждой клетке диаграммы ставится в соответствие двоичный n-мерный набор. Взаимно однозначное соответствие между двоичными наборами и клетками диаграммы устанавливается разметкой последней.
Для функций, зависящих от трех переменных, один из возможных вариантов разметки диаграммы Вейча имеет вид, показанный на рис.1.
Четыре верхних клетки диаграммы соответствуют двоичным наборам, в которых переменная х1 принимает значение 0; четыре нижних клетки соответствуют наборам, в которых переменная х1 принимает значение 1.
Клетки, составляющие левую половину диаграммы, соответствуют наборам, в которых переменная х2 принимает значения 1, а в правой половине находятся клетки, в которых переменная х2 принимает значение 0.
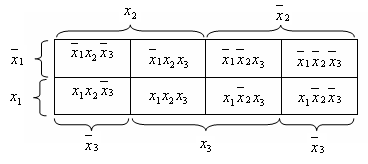
Рис. 1.
Четыре центральные клетки соответствуют наборам, в которых переменная х3 принимает значения 1, а в левом и правом крайних столбцах находятся клетки, в которых переменная х3 принимает значение 0.
На рис. 2 приведены пример разметки диаграммы для логических функций четырех переменных.
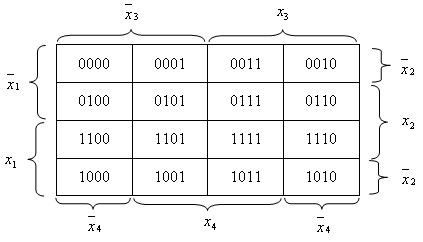
Рис. 2.
Диаграммы Вейча для большего числа переменных могут быть составлены из диаграмм меньшего числа переменных. Например, диаграмму Вейча для пяти переменных можно составить, соединив две диаграммы для четырех переменных. При этом удобно подсоединять их друг к другу одноименными столбцами (рис. 3). Тогда соседними клетками будут также клетки столбцов, симметрично расположенных относительно линии присоединения диаграмм Вейча четырех переменных для одноименных строк.
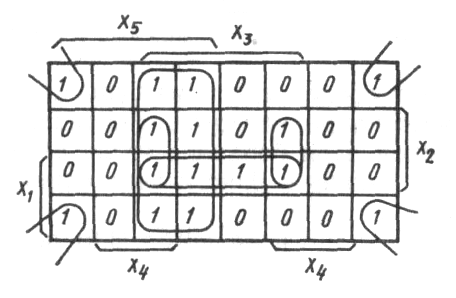
Рис. 3.
В клетки,
соответствующие конституентам единицы
минимизируемой булевой функции,
записываются единицы, а в остальные —
нули. Поэтому исходная минимизируемая
функция первоначально должна быть
представлена в СДНФ. Если функция задана
аналитически, то она приводится к СДНФ
с помощью операции развертывания,
заключающейся в умножении некоторых
членов на выражение вида
.
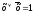Минимизация булевых функций с использованием диаграмм Вейча основывается на отыскании склеивающихся конституент единицы. Для диаграммы Вейча склеивающиеся конституенты единицы располагаются в соседних, вертикально или горизонтально расположенных клетках. Для диаграммы трех переменных (рис. 1) соседними клетками являются также клетки левого и правого столбцов для одноименных строк. Наглядно это можно представить, если наклеить диаграмму на цилиндр так, чтобы левая ее граница совпала с правой.
Для диаграммы Вейча четырех переменных (рис. 2) соседними клетками будут также клетки, расположенные в верхних и нижних строках для одноименных столбцов.
Процесс отыскания минимальной ДНФ заключается в том, чтобы всю совокупность единиц диаграммы Вейча накрыть наименьшим числом наиболее коротких произведений. Для этого соседние клетки диаграммы, содержащие единицы, объединяют в группы (склеиваются).
Каждой такой группе будет соответствовать группа склеивающихся конституент единицы. Причем количество клеток, входящих в одну группу, равно 2k (где k = 1, 2, 3, ...), а каждая клетка, входящая в группу, должна иметь k соседних клеток.
Для получения минимальной ДНФ достаточно выполнить следующие условия:
каждая единичная клетка должна входить хотя бы в одну группу (при этом одна и та же клетка может входить в несколько групп);
в каждую группу должно входить максимальное количество клеток, т.е. ни одна группа, удовлетворяющая обоим вышеприведенным правилам, не должна быть частью другой группы, удовлетворяющей этим же правилам;
количество групп должно быть минимальным.
Рекомендации по минимизации булевых функций с использованием диаграмм Вейча:
1. Рассматриваются поочередно клетки, содержащие единицы, и анализируются всевозможные варианты склеивания. При этом сначала склеивание выполняется только для тех клеток (единиц), для которых вариант склеивания единственный. В результате будут выделены обязательные (или существенные) простые импликанты.
2. Оставшиеся несклеенные клетки (единицы) необходимо склеивать таким образом, чтобы образовать минимальное число групп с максимальным числом клеток в каждой группе.
3. Каждой группе объединенных клеток в минимальной ДНФ будет соответствовать простая импликанта, определяемая как конъюнкция только тех переменных, значения которых постоянны для всех наборов, задающих клетки данной группы.
Группе, состоящей из 2k клеток, соответствует конъюнкция из n – k букв, где n — число переменных в исходной булевой функции.
Пример 1. Найти минимальную ДНФ для булевой функции трех переменных, заданных следующей таблицей истинности(табл.1):
Таблица 1
|
№ на |
х1 |
х2 |
х3 |
z |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
СДНФ для этой функции
.
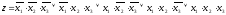Составим диаграмму Вейча (рис. 4)
