
- •1.Показники безвідмовності відновлюваних об’єктів. Математичні моделі безвідмовності.
- •1.1. Поняття потоку відмов
- •1.2. Параметр потоку відмов
- •1.3. Середній наробіток на відмову
- •1.4 Основні математичні моделі безвідмовності
- •1.4.1. Залежність інтенсивності відмов і параметра потоку відмов від наробітку
- •1.4.2. Експонентний розподіл
- •Значення функції
- •1.4.3. Розподіл Вейбулла
- •1.4.4. Нормальний і пересічений нормальний розподіли
- •Значення функції Лапласа
- •2. Показники ремонтопридатності.
- •Зв'язок між показниками ремонтопридатності
- •Гамма-розподіл і розподіл Ерланга
1.Показники безвідмовності відновлюваних об’єктів. Математичні моделі безвідмовності.
1.1. Поняття потоку відмов
Відновлюваний
об'єкт у процесі тривалої експлуатації
може перебувати в кожен момент часу в
одному з станів: працездатному (е0)
або непрацездатному (е1).
Графік стану такого об'єкта й тимчасова
діаграма його функціонування зображені
на рис. 2.5, де
![]() ,
,![]() ,
,![]() -
відповідно наробіток об'єкта (i-1)-м
й i-ми
відмовами й час його відновлення після
i-ї
відмови.
-
відповідно наробіток об'єкта (i-1)-м
й i-ми
відмовами й час його відновлення після
i-ї
відмови.
Під потоком відмов розуміють послідовність моментів виникнення відмов, що чергуються з моментами відновлень (рис. 2.5). Він може характеризуватися властивостями ординарності, стаціонарності й відсутності післядії.

Рис. 2.5
Ординарність потоку означає, що поява одночасно двох і більше відмов неможливі. У математичній формі цю умову записують так:
![]() ,
,
де
![]() - імовірність появи двох і більше відмов
га інтервалі
- імовірність появи двох і більше відмов
га інтервалі![]() .
.
Стаціонарність
потоку полягає в тому, що імовірність
виникнення деякого числа відмов у
проміжку часу
![]() не залежить від положення цієї ділянки
на осі часуt,
а залежить лише від довжини проміжку
не залежить від положення цієї ділянки
на осі часуt,
а залежить лише від довжини проміжку![]() . Математично умову стаціонарності
можна записати в такий спосіб:
. Математично умову стаціонарності
можна записати в такий спосіб:
![]() .
.
Відсутність
післядії означає, що ймовірність
виникнення деякого числа відмов у
проміжку часу
![]() ,
не залежить від того, скільки відмов
виникло до моменту часу
,
не залежить від того, скільки відмов
виникло до моменту часу![]() в проміжку часу
в проміжку часу![]() ,
тобто
,
тобто
![]() .
.
Це
означає, що ймовірність появи
![]() відмов у проміжку часу
відмов у проміжку часу![]() й
й![]() –
у проміжку
–
у проміжку
![]() .
.
Потік відмов, що володіє одночасно властивостями ординарності й відсутності післядії, називається Пуасонівським. Якщо, крім того, він є стаціонарним, то такий потік називається найпростішим. Найпростіші потоки широко використаються в теорії надійності й масового обслуговування.
Використовуючи
поняття потоку відмов, розглянемо
основні показника безвідмовності
відновлюваних об'єктів: параметр потоку
відмов
![]() і середній наробіток на відмову
і середній наробіток на відмову![]() .
.
1.2. Параметр потоку відмов
Як
характеристику потоку відмов використають
провідну функцію потоку
![]() ,
що визначається як математичне очікування
числа відмов за часt,
тобто
,
що визначається як математичне очікування
числа відмов за часt,
тобто![]() ,
деr(t)
– число
відмов за час t.
,
деr(t)
– число
відмов за час t.
Згідно до ДСТУ 2860-94. параметр потоку відмов - це відношення математичного очікування числа відмов відновлюваного об'єкта за досить малий його наробіток до значення цього наробітку.
Відповідно до наведеного визначення

де
![]() – математичне очікування числа відмов
в інтервалі
– математичне очікування числа відмов
в інтервалі![]() ;
;
![]() –імовірність
появи в інтервалі (t,
t+Δt) точно
k
відмов.
–імовірність
появи в інтервалі (t,
t+Δt) точно
k
відмов.
На практиці в більшості випадків можна вважати, що потік відмов об'єкта є ординарним. Тоді вираз для параметра потоку відмов приймає наступний вид:
![]() ,
,
де
![]() –
нескінченно мала величина більш високого
порядку малості, ніж
–
нескінченно мала величина більш високого
порядку малості, ніж
![]() .
.
З
формули (2.15) видно, що параметр потоку
відмов пов'язаний із провідною функцією
потоку
![]() співвідношенням
співвідношенням
![]() .
.
Якщо
випадкові значення наробітку об'єкта
між відмовами мають той самий закон
розподілу із густиною
![]() ,
то параметр потоку відмов виражається
через густина
,
то параметр потоку відмов виражається
через густина![]() наступним рівнянням [7]:
наступним рівнянням [7]:
![]() .
.
Це рівняння не завжди вдається вирішити до кінця. Тут доцільно використати метод послідовних наближень, відповідно до якого роблять послідовні обчислення за формулою
![]()
доти,
поки значення
![]() й
й![]() не будуть збігатися. Як нульове наближення
не будуть збігатися. Як нульове наближення![]() рекомендується вибирати інтенсивність
відмов
рекомендується вибирати інтенсивність
відмов
![]() .
.
На
рис. 2.6 проведена залежність
![]() при нормальному розподілі наробітку
об'єкта між відмовамиТ.
при нормальному розподілі наробітку
об'єкта між відмовамиТ.
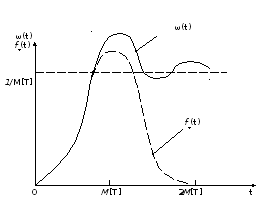
Рис.2.6.
З рисунку видно, що спочатку параметр потоку відмов робить ряд коливань, а потім прагне до деякого значення, що встановилося:
![]() .
(2.16)
.
(2.16)
Тривалість
коливань обернено пропорційна середньому
квадратичному відхиленню випадкової
величали T.
Помітно, що вираз (2.16) справедливий при
будь-якому законі розподілу
![]() .
.
Якщо
випадкова величина T
підлягає експонентному закону з
параметром λ,
то неважко показати, що
![]() .
.
Статистична оцінка параметра потоку відмов може бути визначена за формулою
 ,
(2.17)
,
(2.17)
де
![]() – число об'єктів, що беруть участь у
випробуваннях;
– число об'єктів, що беруть участь у
випробуваннях;
![]() –число
відмов
–число
відмов
![]() -го
об'єкта, що виникли в проміжку
-го
об'єкта, що виникли в проміжку
![]() .
.
