12

Державний університет телЕкомунікацій

КАФЕДРА ВИЩОЇ МАТЕМАТИКИ

Затверджую

Завідувач кафедри

професор ___________ О. В. Барабаш

____ серпня 2014 року

СЕМЕСТР 2

Л Е К Ц І Я № 1

МОДУЛЬ 1

Тема 1: Елементи лінійної алгебри

Тема лекції: Матриці та визначники

з навчальної дисципліни

основи вищої математики та теорії імовірностей

напряму підготовки соціологія

освітньо-кваліфікаційного рівня бакалавр

Лекція розроблена

Кандидатом фізико – математичних наук, доцентом Омецінською О.Б.

Обговорено на засіданні кафедри

Протокол № 1

28 серпня 2014 року

Київ – 2014

основи вищої математики та теорії імовірностей

Лекція № 1. Матриці та визначники

План лекції:

Вступ.

1. Матриці, алгебраїчні дії над ними.

2. Визначники 2-го та 3-го порядку.

3. Розклад визначника вищого порядку за елементами рядка (стовпця).

4. Властивості визначників

Заключення.

Література

1. Дубовик В. П., Юрик І.І. Вища математика. К: Ігнатекс-Україна, 2013, 648 с.

2. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум. Київ. – 2005, 535 с.

Завдання на самостійну роботу

1. Вивчити основні положення за підручником [1] (стор. 6-20) або за підручником [2] (стор. 35-46) та наступним текстом лекції.

2. Набути первинних навичок обчислення визначників 2-3 порядків.

Текст лекції

Вступ

Предметом розгляду лекції є матриці та визначники - об’єкти вивчення з Розділу вищої математики Лінійна алгебра. Основна складова частина цього Розділу - теорія систем лінійних алгебраїчних рівнянь (СЛАР), які описують широке розмаїття прикладних задач технічних, економічних тощо.

1. Матриці, алгебраїчні дії над ними

Означення 1. Матриця розмірності mхn – таблиця упорядкованих чисел або інших об’єктів, розташованих в m рядках та в n стовпцях. Матриці позначають великими літерами А, В, С або в розгорненому вигляді вказують в круглих чи квадратних дужках таблицю її елементів.

Матриця називається квадратною порядку n, якщо кількість її рядків однакова з кількістю стовпців і дорівнює n.

Приклад 1. Нехай задані матриці

; ;

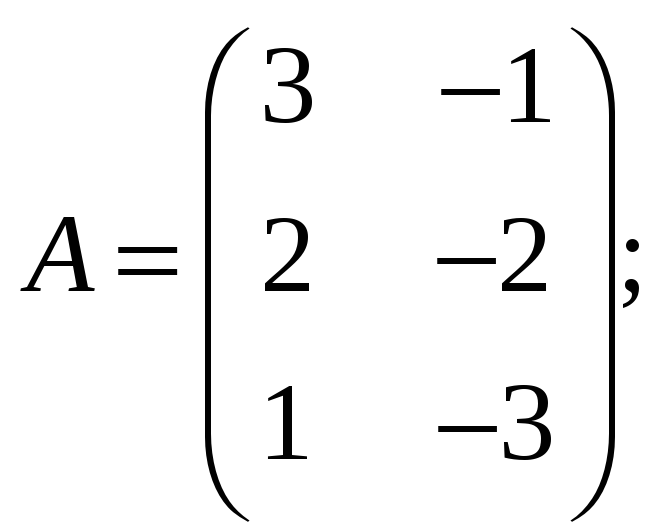
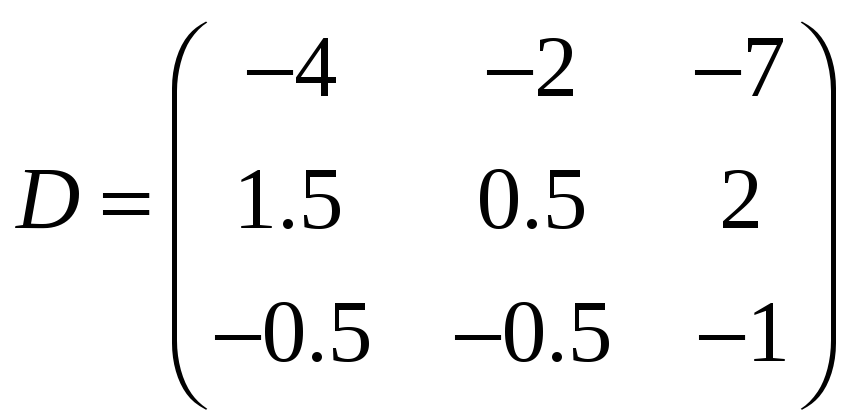
Матриця А має розмірність 3х2, матриця В розмірності 1х4 – матриця-рядок, матриця С розмірності 3х1 – матриця-стовпець, матриця D – квадратна порядку 3.

Матриця, всі елементи якої нулі, називається – нульовою або нуль-матрицею. Позначення нульової матриці – 0.

Елементи квадратної матриці, що розташовані на діагоналі матриці, яка проходить з лівого верхнього кута до правого нижнього кута, утворюють головну діагональ матриці. Альтернативою є побічна діагональ матриці.

Квадратна матриця є діагональною, якщо всі її елементи дорівнюють 0, крім елементів головної діагоналі, з-посеред яких принаймні один елемент є відмінним від 0.

Діагональна матриця, усі елементи головної діагоналі якої дорівнюють 1, називається одиничною і позначається Е.

У загальному вигляді елементи матриці А позначають літерою із двома індексами а_ij, де перший індекс i вказує номер рядка, в якому знаходиться цей елемент, а другий індекс j – номер стовпця. Наприклад, а₂₃ – елемент матриці А, який знаходиться на перетині її другого рядка і третього стовпця.

У розгорненому вигляді матриця А розмірності mхn записується

або у компактній формі А=(а_ij), де i =1,2,… m; j=1,2,…n.

Матриці А та В називаються рівними, якщо вони мають однакову розмірність і їхні відповідні елементи рівні, тобто а_ij=в_ij для усіх i та j.

Якщо в матриці А рядки, із збереженням їхньої нумерації, записані відповідними стовпцями, то одержана матриця називається транспонованою і позначається А^Тр. Ця операція називається транспонуванням матриці А.

Наприклад,

Якщо , тоді .

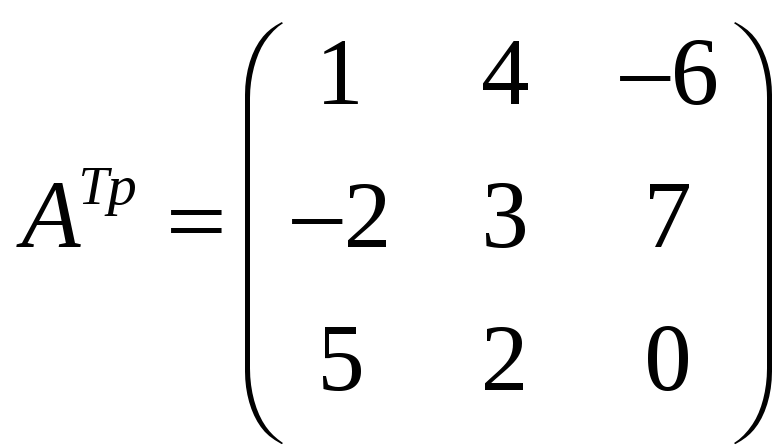Тобто, матриця А^Тр, транспонована до квадратної матриці А, є симетричним відображенням елементів матриці А відносно її головної діагоналі.