24. Электрическое поле и его характеристики

Эл-кое поле-разновидность материи, посредством которой осущ-ся силовое воздействие на эл-кие заряды нах-ся в этом поле. Силовая хар-ка – напряженность (отношение силы, действующей в данной точке поля на точечный заряд к этому заряду) Е=F/q. Эл-кое поле графически удобно представлять силовыми линиями, касательные к которым совпадают с направлением вектора напряженности в соотв-х точках поля. Энергетическая хар-ка – потенциал. Работа сил электростатического поля не зависит от траектории по которой перемещается заряд в этом поле ( такое поле – потенциальное. Работа сил электростатического поля по перемещению заряда по замкнутой траектории равна нулю. Работа сил электростатического поля не зависит от: траектории заряда, нач и конечн. Точек перемещений, напряженности поля. Разность потенциалов – отношение работы, совершаемой силами поля при перемещении точечного положительного заряда из одной точки поля в другую, к этому заряду: U₁₂ = φ1 – φ2=A\q. Потенциалы в виде эквипотенциальных пов-стей. Силв. линии и эквипотенц. Пов-сти взаимно перпендик. Если поле создано N точечными зарядами, то напр-сть в некоторой точке можно вычислить как векторную сумму напр-стей полей , созд-х каждым зарядом в этой точке отдельно(принцип суперпозиции): E=∑^N_i=1Ei , а эл-кий потенциал как алгебр. Суммупотенц-в от каждого заряда.

25. Электрич.диполем наз. систему, сост. из 2 равных, но противополож. по знаку то­чечных электрич. зарядов, расп. на некотором расстоянии друг от друга (плечо диполя). Основной харак-теристикой диполя (рис. 12.5) явл. его электрич. момент (дипольный момент) — вектор, рав­ный произ-нию заряда на плечо диполя l, направленный от от­риц. заряда к полож-ному: Единицей электрич. момента диполя явл. кулон-метр.

Поместим диполь в однород. электрич.поле напряженностью (рис. 12.6).

На каждый из зарядов диполя действуют силы и , эти силы равны по модулю, противоположно направлены и создают момент пары сил. Как видно из рисунка, он равен или в векторной форме :

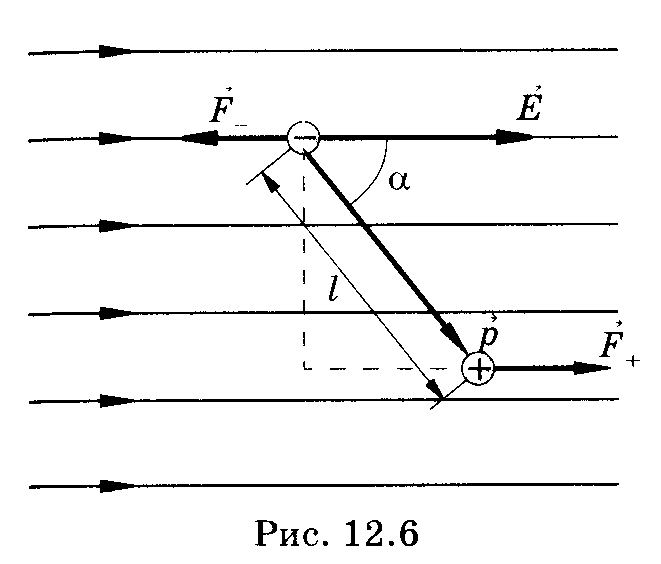
Таким образом, на диполь в однород. электрич. поле дей-ствует момент силы, зависящий от электрич. момента и ориентации диполя, а также напряженности поля. . Диполь в неоднородном электрическом поле. В неод­нор. электрич. поле вращающее действие тоже имеет место, и диполь ориентир-ся вдоль соответ. линии поля. Однако в этом случае значения сил, д-щих на по­люса диполя (силы F⁺ и F^- на рис. 18.3), не одинаковы, и их сумма не равна нулю.=> возн. результирующая сила, втяг-щая диполь в область более сильного поля..

Результирующая сила зависит от изменения напряженности приходящегося на единицу длины диполя. Обозначим Е⁺ и Е^- модули напряженности поля у положит. и отриц. полюсов. Тогда Т.к. плечо диполя мало, то приближенно можно считать, что где dE/dl — градиент поля. Таким образом, на диполь, который ориентирован вдоль си­ловой линии и имеет момент р, дей-ет сила, втягивающая его в область поля с большей напряж-тью:

Электрическое поле диполя: Сам диполь явл. источником электрич. поля, на­пряженность кот. зависит от дипольного момента р, от ди­электрической прониц-сти среды ε и геометрич. пара­метров. Пусть диполь нах. в непроводящей бесконечной среде и некоторая точка А удалена от его центра на расстояние Обозначим через α угол между вектором р и направ­лением на эту точку. Тогда потенциал, создаваемый диполем в точке Л, опр-ся следующей формулой (рис. 18.4):

Рис: потенциал эл.поля,

созд-го диполем

26. Диполь явл. частным случаем с-мы электрич. заря­дов, облад-щей определ. сим-метрией. Можно указать еще примеры симметр. систем зарядов электрич. мульти-поли. Они бывают разных порядков (l = 0,1,2). Число зарядов мультиполя опр. выра-жением 2^l. Так, мультиполем нулевого порядка (2° = 1) явл. одиночный точечный заряд (рис.а), м-лем первого порядка (2¹ = 2) — диполь, мультиполем II п-ка (2² = 4) — квадруполь (рис.б), м-лем III п-ка (2³ = 8) — октуполь (рис. в)