MECHANICS_physicists_2011_ / 408_19_Zviaz_vahanni_A5_2010
.pdfГродзенскі дзяржаўны універсітэт імя Янкі Купалы
Кафедра агульнай фізікі Лабараторыя механікі ауд. 408
Лабараторная работа №19
ВЫВУЧЭННЕ ВАГАННЯЎ ЗВЯЗАНЫХ ФІЗІЧНЫХ МАЯТНІКАЎ
для студэнтаў спецыяльнасці “ФІЗІКА”
Гродна, 2010
1
ВЫВУЧЭННЕ ВАГАННЯЎ ЗВЯЗАНЫХ ФІЗІЧНЫХ МАЯТНІКАЎ
Мэта работы:
Доследнае вызначэнне характарыстык звязаных фізічных маятнікаў.
Прылады і абсталяванне:
Прылада для вывучэння звязаных ваганняў, секундамер, лінейка, тэхнічныя вагі.
Тэарэтычныя асновы
Два фізічных маятніка, звязаныя паміж сабой спружынай, з’яўляюцца прасцейшым прыкладам звязанай сістэмы.
Кожны свабодны фізічны маятнік, як вядома, валодае дзвюма ступенямі свабоды, гэта значыць для апісання яго руху неабходна два параметры – вуглы змяшчэння у двух узаемна перпендыкулярных плоскасцях.
Сістэма з двух маятнікаў апісваецца чатырма параметрамі і, такім чынам, мае чатыры ступені свабоды. Калі ваганні, якія адпавядаюць кожнай са ступеняў свабоды, незалежныя, то задача апісання руху сістэмы з’яўляецца толькі кінематычнай, гэта значыць задача зводзіцца да раскладання складанага руху на суму больш простых рухаў.
Калі паміж рухамі па розных ступенях свабоды ёсць дынамічная сувязь , пры якой рух па адной ступені свабоды выклікае дынамічныя змены ў астатніх ступенях свабоды, адбываецца абмен энергіяй паміж ступенямі свабоды, што прыводзіць да новых фізічных з’яў, якія не назіраюцца пры незалежных ваганнях.
У гэтай лабараторнай рабоце вывучаюцца ваганні сістэмы з двух звязаных аднолькавых фізічных маятнікаў (мал. 1). Такая сістэма мае толькі дзве ступені свабоды. Для гэтага канструкцыя падвесу кожнага маятніка дазваляе вагацца толькі у вертыкальнай плоскасці, якая праходзіць праз лінію, што злучае пункты падвесу.
2
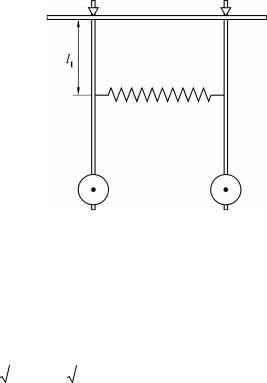
Як вядома, для свабоднага матэматычнага маятніка ўраўненне момантаў мае наступны выгляд:
J |
dw |
= -mgl ×sin a |
(1) |
|
dt |
||||
|
|
|
Гэтае ж ўраўненне будзе апісваць ваганні і фізічнага маятніка, толькі з той розніцай, што ва ўраўненні (1) l – прыведзеная даўжыня фізічнага маятніка.
Мал. 1. |
sin a » a - a3 /3!+.... і |
|
Калі раскласці sin α у рад |
Тэйлара |
|
абмежавацца толькі лінейным |
членам, а |
таксама ўлічыць, што |
момант інерцыі фізічнага маятніка J = ml2 ( l – прыведзеная даўжыня фізічнага маятніка), то атрымаем так званае ўраўненне гарманічнага асцылятара:
ml |
2 |
&& |
|
* |
|
&& |
|
|
2 |
a = 0 , |
(2) |
|||||
|
a + mgla = 0 |
|
|
або a + w |
|
|||||||||||
дзе |
w = |
|
= |
|
|
– цыклічная частата ўласных ваганняў |
||||||||||
mgl / J |
g / l |
|||||||||||||||
фізічнага маятніка. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2a |
|
||
* |
|
|
& |
&& |
|
|
|
|
|
da |
|
|
|
|||
|
|
|
|
|
|
|
|
dt |
³ dt 2 |
|
||||||
|
Çàï³ñû α ³ α азначаюць |
– адпаведна першую ³ другую |
||||||||||||||
вытворную па часе,
3
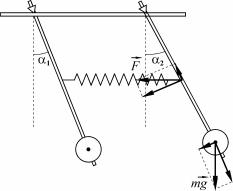
У выпадку звязаных маятнікаў на кожны з іх будзе дзейнічаць
дадатковая сіла з боку спружыны F , якая пры невялікіх адхіленнях маятнікаў можа быць разлічана па закону Гука:
F = kDx = kl1 (a2 - a1 ) , дзе l1 – адлегласць ад восі падвесу
маятніка на месца замацавання спружыны (глядзі мал. 1).
Гэтая сіла стварае дадатковы момант, які неабходна улічваць, і тады замест (2) атрымаем (гл. мал. 2) для першага і другога маятнікаў ураўненні руху будуць мець выгляд адпаведна.
ì |
2 && |
|
= -mgl sin a1 |
+ Fl1 cosa1; |
|
|||||||||||
ïml |
a1 |
(3) |
||||||||||||||
í |
2a&& |
|
= -mgl sin a |
|
|
+ Fl cosa |
|
|||||||||
ïml |
2 |
2 |
|
2 |
. |
|||||||||||
î |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
Калі ўлічыць, што |
|
для |
малых вуглоў sin α ≈ α , cosα ≈ 1, то |
|||||||||||||
сістэма (3) набудзе выгляд |
|
|
|
|
||||||||||||
ì |
2 && |
|
|
|
|
|
2 |
(a2 - a1 ); |
|
|
||||||
ïml |
a1 |
= -mgla1 + kl1 |
|
|
(4) |
|||||||||||
í |
2 && |
|
= -mgla |
|
+ kl |
2 |
(a |
|
- a |
|
). |
|||||
ïml |
a |
2 |
2 |
|
|
2 |
1 |
|
||||||||
î |
|
|
|
|
1 |
|
|
|
|
|
|
|||||
Мал. 1.
З (4) атрымаем |
|
|
|
||||||||
ì |
|
|
|
g |
|
|
kl12 |
|
|
(a2 - a1 )= 0; |
|
ïa1 |
+ |
|
|
a1 |
- |
|
|
|
|
||
ï |
&& |
|
|
l |
|
|
ml2 |
(5) |
|||
í |
|
|
|
g |
|
|
|
kl12 |
|||
ï |
|
|
|
|
|
|
(a2 - a1 )= 0. |
||||
ïa2 |
+ |
|
|
a2 |
- |
|
|
|
|||
|
|
|
|
2 |
|||||||
î |
&& |
|
|
l |
|
|
|
ml |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пасля складання і адымання ўраўненняў сістэмы (5), атрымаем
4
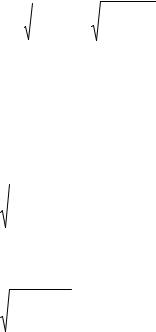
ìd 2 |
(a |
1 |
+ a |
2 |
) |
+ |
|
g |
(a1 + a2 )= 0; |
|
|
|
|||
ï |
|
|
|
|
|
|
|
|
|
||||||
|
dt 2 |
|
|
l |
|
|
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
||||
íd 2 (a - a |
|
) |
+ |
|
2kl2 |
(a1 - a2 )+ |
g |
(a1 |
- a2 )= 0. |
||||||
ï |
|
|
1 |
2 |
2 |
|
|
|
|
2 |
|
||||
ï |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
î |
|
dt |
|
|
|
|
|
ml |
|
|
l |
|
|
||
Увядзём пазначэнні y1 = a1 + a2 і y2 = a1 - a2 і атрымаем
ìd 2y1 |
+ |
g |
|
y1 = 0; |
|
ìd |
2y |
1 |
|
+ w2y |
|
|
|
|||||||||||
ï |
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
= 0; |
|||||||||
|
2 |
|
l |
|
|
|
|
|
|
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
ï dt |
|
|
|
|
|
|
|
|
|
|
|
ï |
dt |
2 |
|
|
|
|
|
|
||||
í |
d 2y |
|
|
|
æ |
2kl2 |
|
g ö |
|
або í |
|
|
|
|
|
|
|
|||||||
ï |
2 |
|
|
|
|
ï |
d |
2 |
y2 |
|
|
|
|
|
||||||||||
|
|
|
+ ç |
|
|
1 |
+ |
|
÷y2 |
= 0. |
|
|
+ w2y |
|
= 0. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ï |
|
2 |
|
|
|
|
2 |
|
ï |
|
|
|
|
2 |
||||||||||
dt |
|
|
|
ç |
|
|
|
÷ |
|
dt |
2 |
|
2 |
|
|
|||||||||
î |
|
|
|
|
è ml |
|
|
l ø |
|
î |
|
|
|
|
|
|
|
|||||||
(6)
(7)
|
|
g |
|
|
|
|
g |
|
2kl2 |
|
|
дзе w = |
|
|
, w |
2 |
= |
|
+ |
1 |
. |
(8) |
|
|
|
|
|||||||||
1 |
|
l |
|
|
|
l |
|
ml2 |
|
||
|
|
|
|
|
|
|
|
||||
Ураўненні (7) – гэта ўраўненні гарманічнага асцылятара, і іх рашэнне мае выгляд:
y1 = A0 sin(w1t + j1 ), |
|
|
|
|
|
|
|
(9) |
|||||||
y2 = B0 sin(w2t + j2 ), |
|
|
|
|
|
|
|
(10) |
|||||||
дзе A0 , B0 , j1 і j2 |
вызначаюцца з пачатковых умоў пры t = 0 : |
||||||||||||||
y10 = A0 sin j1 |
, |
y10 |
= A0w1 cosj1 , |
|
|
|
|
|
(11) |
||||||
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
адкуль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
& |
2 |
|
|
|
y10w1 |
|
|
|
dy1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
y10 |
|
|
|
|
|
|
|
|
|
|||||
A0 = y10 |
+ |
|
|
|
, tgj1 = |
|
, дзе y10 |
= |
|
|
. |
(12) |
|||
|
2 |
|
|
|
|||||||||||
|
|
|
w1 |
|
|
|
y10 |
|
& |
|
dt |
t=0 |
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
Адпаведна |
|
, |
|
y20 |
= B0w2 cosj2 , |
|
|
|
|
|
(13) |
||||
y20 = B0 sin j2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
адкуль
2 |
|
& 2 |
|
y20w2 |
|
dy |
2 |
|
|
|
|
|
|||||
|
y20 |
|
|
|
||||
B0 = y20 |
+ |
|
, tgj2 = |
|
, y20 = |
|
|
|
2 |
|
|
|
|
||||
|
|
w2 |
|
y20 |
& |
dt |
|
|
|
|
|
|
& |
|
|
|
|
Вяртаючыся да папярэдніх пазначэнняў і атрымаем
a1 + a2 = A0 sin(w1t + j1 ), a1 - a2 = B0 sin(w2t + j2 ),
. (14)
t=0
зулікам (9) і (10),
(15)
(16)
5
адкуль атрымаем
α1 = Asin(ω1t + ϕ1 )+ Bsin(ω2t + ϕ2 ), |
(17) |
α2 = Asin(ω1t + ϕ1 )− Bsin(ω2t + ϕ2 ). |
(18) |
Такім чынам, ваганні кожнага маятніка ўяўляюць сабой суперпазіцыю двух гарманічных ваганняў ψ1 і ψ2 , якія атрымалі назву нармальных ваганняў.
Амплітуды A і B і фазы ϕ1 і ϕ2 вызначаюцца з пачатковых умоў ( t = 0 ) і будуць роўныя
|
|
A0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
& |
|
& |
2 |
|
|
|
|
|
A = |
|
= |
(α |
01 |
+ α |
02 |
)2 + |
|
(α01 |
+ α02 ) |
|
|
(19) |
||||||||||
2 |
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
B0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
& |
|
& |
2 |
|
|
|
|
|
B = |
|
= |
(α01 − α02 )2 + |
|
(α01 |
− α02 ) |
|
|
(20) |
||||||||||||||
|
2 |
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω22 |
|
|
|
|
|
||
tgϕ = |
|
(α01 + α02 )ω1 |
; |
tgϕ |
|
|
= |
(α01 − α02 )ω2 |
(21) |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
& |
& |
|
|
|
|
|
2 |
|
|
|
& |
& |
|
|
|
|
|
|
|
|
|
|
(α01 |
+ α02 ) |
|
|
|
|
|
|
|
(α01 |
− α02 ) |
|
|||||||
Доследная прылада
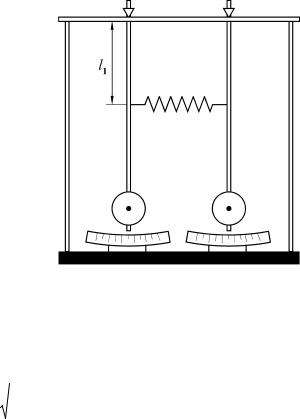
Прылада складаецца з металічнай рамы (мал. 3), на якой падвешаны два аднолькавыя фізічныя маятнікі ў выглядзе металічных стрыжняў, да якіх зверху замацавана прызма, а знізу – грузы (чачавіцы) некаторай масы. На адлегласці l1 ад пункта
падвесу ў стрыжнях замацаваная лёгкай спружына сувязі, даўжыня якой у недэфармаваным стане роўная адлегласці паміж стрыжнямі маятнікаў у неадхіленым стане.
Тэорыя метаду
Разгледзім канкрэтныя прыклады ваганняў звязаных маятнікаў.
1) Няхай у пачатковы момант часу t = 0 абодва маятнікі адхілены ад становішча раўнавагі ў адзін і той жа бок на адзін і той жа вугал роўны α10 = α20 . Тады з пачатковых умоў атрымаем α10 = α20 ;
α10 |
= α20 = 0 , таму A = α10 ; B = 0 ; ϕ1 = ϕ2 = π / 2 . |
& |
& |
|
6 |
|
|
Мал. 3. Доследная прылада |
|
α1 |
(t) = α10 cosω1t |
(22) |
|
α2 (t) = α20 cosω1t |
|||
|
|||
Гэта значыць, што два маятнікі сінхронна вагаюцца з першай нармальнай частатой
ω = |
|
g |
|
, |
(23) |
|
|
||||
1 |
|
l |
|
||
дзе l |
|
|
|||
– прыведзеная даўжыня фізічнага маятніка. |
|
||||
У гэтым выпадку спружына сувязі не расцягваецца і не аказвае ўплыву на рух кожнага маятніка.
2) Абодва маятніка адхілены на аднолькавы пачатковы вугал α10 , але ў процілеглыя бакі ад становішча раўнавагі (пры t = 0 ). У
гэтым |
выпадку α10 |
= −α20 ; |
α10 |
= α20 |
= 0 ; |
A = 0 ; |
B = α10 ; |
|
|
|
& |
& |
|
|
|
ϕ1 = ϕ2 |
= π / 2 . Такім |
чынам, |
ураўненні |
руху |
маятнікаў |
будуць |
|
мець выгляд: |
|
|
|
|
|
|
|
α1 (t) = α10 cosω2t , |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
a2 (t) = -a20 cosw2t |
(24) |
Гэта значыць, абодва маятнікі вагаюцца з другой нармальнай частатой
|
|
g |
|
2kl2 |
|
|
w2 |
= |
|
+ |
1 |
. |
(25) |
l |
|
|||||
|
|
|
ml2 |
|
||
У выпадку фізічных маятнікаў трэба мець на ўвазе:
w2 = 
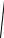gl + 2klJ12 , дзе J – момант інерцыі маятніка адносна восі вярчэння.
3) Няхай у пачатковы момант часу ( t = 0 ) другі маятнік знаходзіцца ў стане спакою, а першы маятнік адхілены на
пачатковы вугал a01 . |
Тады |
|
a02 |
= a02 |
= 0; a |
01 ¹ 0; a01 = 0 |
адкуль |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
& |
|
|
|
A = |
a01 |
; B = |
a01 |
; tgj = tgj |
2 |
= ¥ ; j = j |
2 |
= p / 2 . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для першага маятніка, такім чынам, атрымаем закон руху |
|
||||||||||||||||||||||
a |
(t) = |
a |
01 (cosw t + cosw |
t) |
= a |
|
æ w |
2 |
- w |
ö |
æ w |
2 |
+ w |
ö |
|||||||||
|
|
01 |
cosç |
|
|
1 |
t ÷cosç |
1 |
t ÷ . |
||||||||||||||
1 |
|
|
2 |
|
1 |
2 |
|
|
|
è |
|
2 |
|
ø |
è |
|
2 |
ø |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Калі сувязь паміж маятнікамі лічыць слабой, гэта значыць, што
mgla >> kl2Da , |
атрымаем, |
што |
w » w |
2 |
і |
||
|
|
1 |
|
|
1 |
|
|
Dw = w |
2 |
- w << w'= w1 + w2 . |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
У гэтым выпадку (26) апісвае так званыя біцці двух блізкіх частот, гэта значыць вы можаце разгледзець (мал. 4) як ваганні, якія
адбываюцца |
з |
перыядам T = |
2p |
= |
4p |
амплітуда якіх |
|||||
|
|
||||||||||
|
|
|
|
|
|
1 |
|
w' |
|
w1 + w2 |
|
|
|
|
|
|
|
|
|
|
|
||
павольна (у адносінах да T1 ) змяняецца з цягам часу па закону |
|||||||||||
a0 cos |
Dwt |
з перыядам: |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
Tб = |
|
|
2p |
(Tб |
>> T1 ). |
|
|
|
|
(27) |
|
w2 |
- w1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
8 |
|
|
|
|
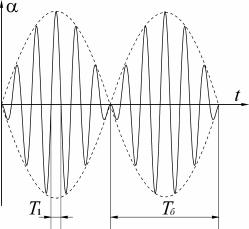
Пры гэтым улічваецца, што максімум амплітуды дасягаецца
двойчы за перыяд, які адпавядае частаце w2 - w1 . 2
Для другога маятніка, які знаходзіцца у пачатковы момант часу у спакоі, аналагічным чынам атрымаем
a |
|
(t) = |
a |
01 |
(cosw t - cosw |
t) = -a |
|
æ Dw |
ö |
(28) |
||
2 |
|
01 |
sinç |
|
t ÷sin w't |
|||||||
|
|
2 |
1 |
2 |
|
è |
2 |
ø |
|
|||
|
|
|
|
|
|
|
|
|||||
Парадак выканання работы:
1.Вызначце перыяды ўласных ваганняў кожнага маятніка паасобна. Для гэтага пры дапамозе секундамера вызначце час 10-
50ваганняў (дакладную колькасць удакладніце ў выкладчыка або лабаранта) кожнага маятніка (здыміце спружыну сувязі пры гэтым).
2.Разлічыце перыяды T1 абодвух маятнікаў. Пераканайцеся, што
становішчы грузаў на стрыжнях падабраны так, што перыяды ваганняў абодвух маятнікаў практычна супадаюць. Калі ж перыяды не супадаюць, падбярыце становішча грузаў так, каб гэтая ўмова ўсё ж такі выканалася. Пры неабходнасці паўтарыце пп. 1-2.
9
3. Па сярэдняму значэнню перыяду T1 вызначце першую
нармальную (уласную) частату ваганняў ω1 = 2π .
T1
4.Усталюйце спружыну сувязі для вымярэння частаты звязаных ваганняў. Калі адзін маятнік замацаваць, а другому надаць вагальны рух, тады частата, з якой вагаецца маятнік, называецца парцыяльнай частатой. Прытрымліваючы адзін маятнік, другі адхіліце на некаторы вугал і адпусціце. Пры дапамозе секундамера вызначце час 20-30 ваганняў маятніка (дакладную колькасць удакладніце ў выкладчыка або лабаранта).
5.Разлічыце першую парцыяльную цыклічную частату.
6.Аналагічна, прытрымліваючы другі маятнік, вызначце другую парцыяльную частату.
7.Параўнайце значэнні вымераных частот з разлічаным па выразе
|
|
|
|
|
g |
|
|
|
2kl2 |
|
|
g |
|
|
2kl2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
значэннем |
|
ω = |
|
|
|
+ |
|
|
|
1 |
= |
|
|
|
|
+ |
|
|
1 |
, |
дзе l |
|
– |
|
прыведзеная |
|||||||||
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
ml2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
даўжыня фізічнага маятніка, |
J – яго момант інерцыі. |
|
|
|
|
|||||||||||||||||||||||||||||
Калі ўлічыць, што момант інерцыі маятніка складаецца з момантаў |
||||||||||||||||||||||||||||||||||
інерцыі стрыжня і грузу, |
|
то з выкарыстаннем метаду ваганняў |
||||||||||||||||||||||||||||||||
(лабараторная работа №8 “Вызначэнне моманту інерцыі дыска”) |
||||||||||||||||||||||||||||||||||
можна |
|
|
|
|
|
|
|
атрымаць |
|
|
|
|
|
|
|
|
адпаведны |
|
|
|
|
выраз |
||||||||||||
J = J |
|
+ J |
|
= |
m d |
1 |
gT 2 |
+ |
m |
2 |
d |
2 |
gT 2 |
|
= (m d |
|
+ m |
|
|
|
) |
gT 2 |
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
, |
||||||||||||||||
|
|
|
4π2 |
|
|
|
4π2 |
|
|
|
|
4π2 |
||||||||||||||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
|
2 |
|
|
|||||||||||
дзе m1 і m2 масы, d1 |
і d2 |
|
|
адлегласці ад восей вярчэння да |
||||||||||||||||||||||||||||||
цэнтраў мас стрыжня |
і |
грузу, T – |
перыяд |
уласных ваганняў |
||||||||||||||||||||||||||||||
маятніка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Каб знайсці прыведзеную даўжыню маятніка дастаткова скарыстацца суадносінай J = ml 2 .
8. Каэфіцыент жорсткасці k спружыны знайдзіце статычным метадам з выкарыстаннем закона Гука. Для гэтага неабходна вызначыць велічыню дэфармацыі спружыны пад дзеяннем грузу вядомай масы, якая вісіць вертыкальна (масу грузу неабходна вызначыць на тэхнічных вагах).
10