АХД 2 / Sposoby_stokhasticheskogo_faktornogo_analiza

Приложение 2

Способы измерения влияния факторов в стохастическом анализе

1. Расчет параметров уравнения прямой линии

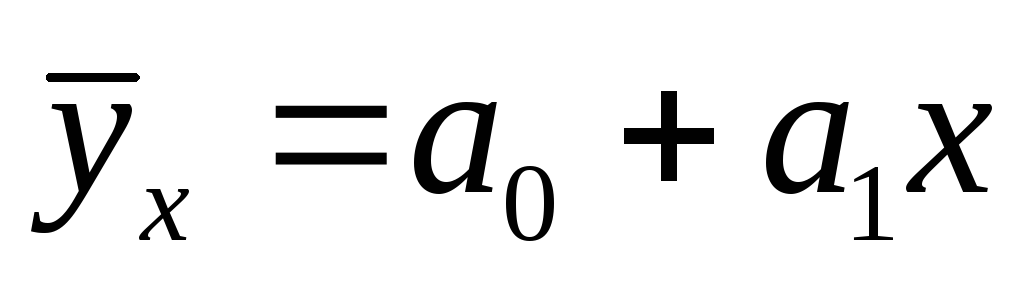
Если результативный признак с увеличением факторного равномерно возрастает или убывает, то такая зависимость является линейной и параметры уравнения прямой могут быть определены по методу наименьших квадратов путем решения системы нормальных уравнений:

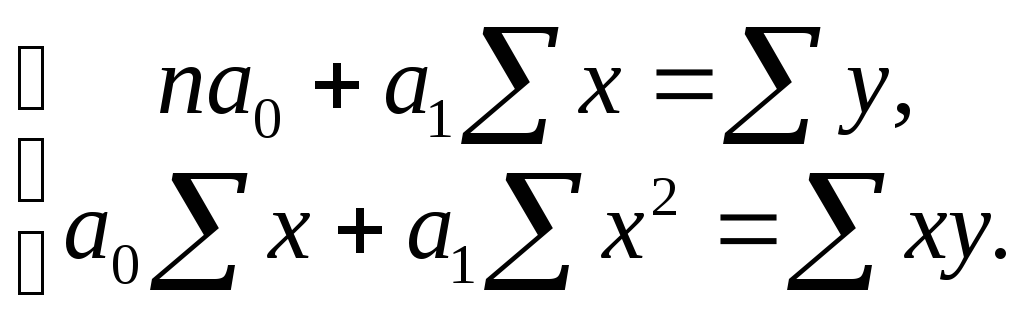
или по следующим формулам: ; .

2. Расчет параметров уравнения параболы второго порядка

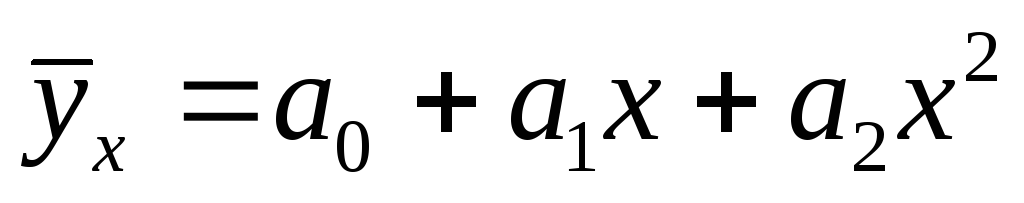
Если связь между признаками нелинейная и с возрастанием признака происходит ускоренное возрастание или убывание результативного признака, то корреляционная зависимость может быть выражена параболой, параметры которой находятся из системы нормальных уравнений:

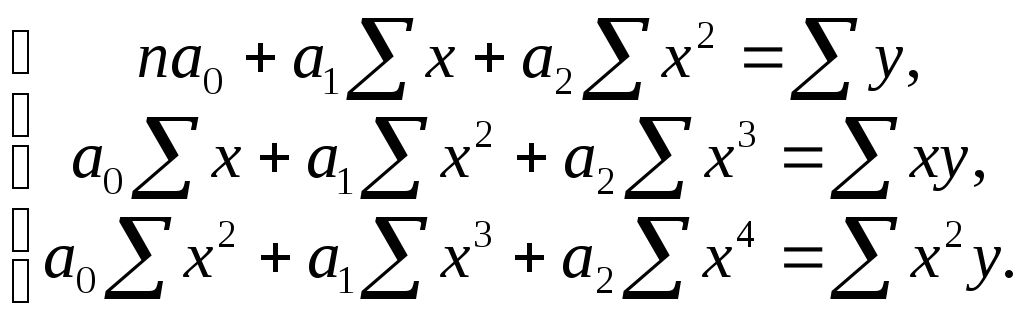
3. Расчет параметров уравнения гиперболы

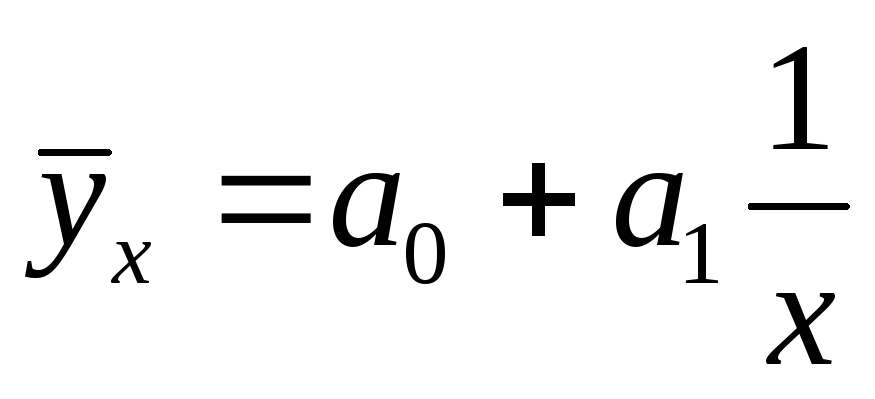
Если результативный признак с увеличением факторного признака возрастает или убывает не бесконечно, а стремиться к конечному пределу, то для анализа такого признака применяется уравнение гиперболы, параметры которого определяются из системы нормальных уравнений:

4. расчет параметров степенной функции

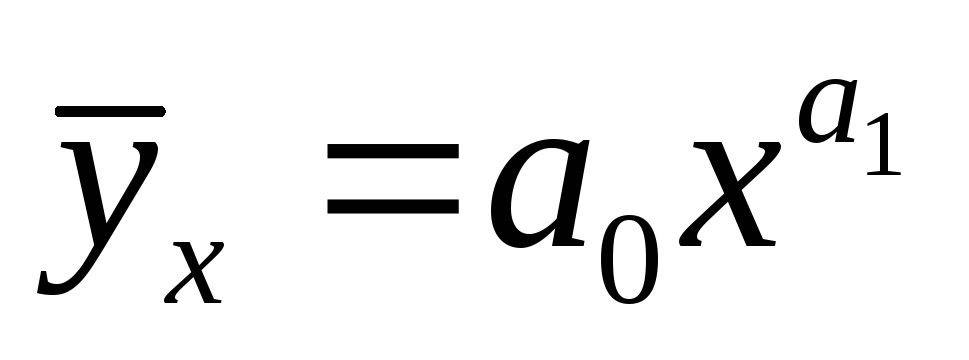
Степенная функция применяется для характеристики слабо нелинейной связи между результативным и факторным признаками. Для определения параметров степенной функции методом наименьших квадратов степенную функцию необходимо привести к линейному виду путем логарифмирования.

В результате логарифмирования получается уравнение вида

.

Путем замены ; ; получаем уравнение связи в виде , для нахождения параметров которого необходимо решить систему уравнений:

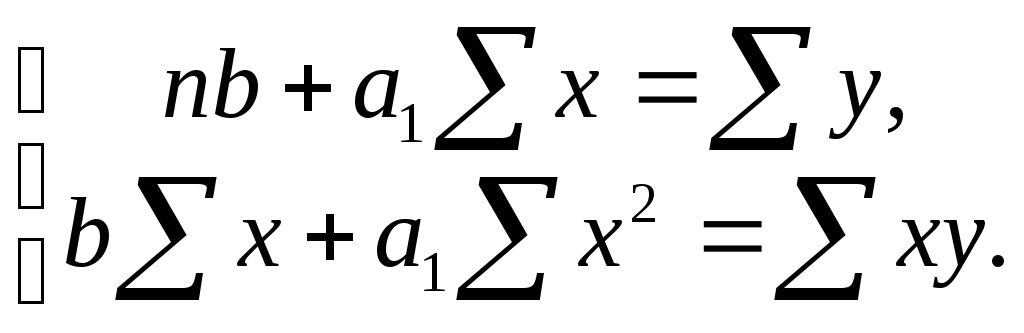
5. Расчет параметров уравнения множественной регрессии с двумя независимыми переменными 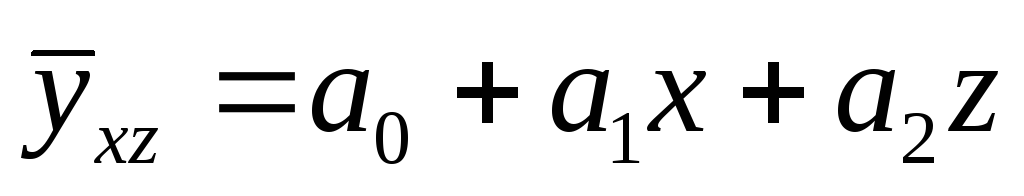осуществляется методом наименьшим квадратов. Параметры уравнения определяются из системы нормальных уравнений:

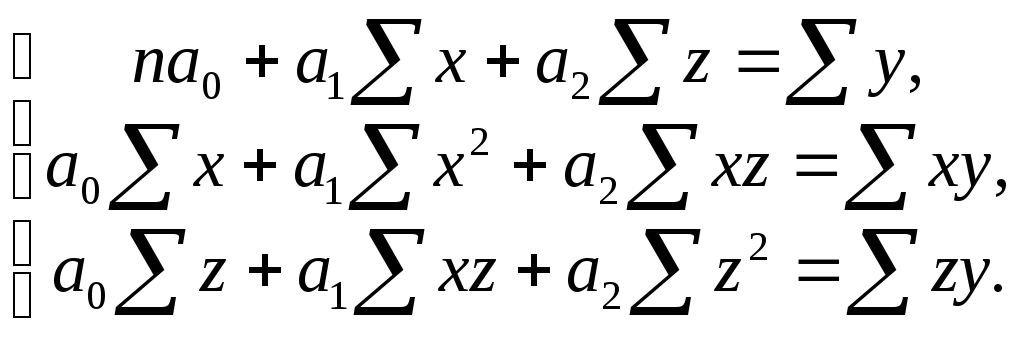
6. При линейной зависимости между признаками для определения тесноты корреляционной связи применяется коэффициент корреляции. Наиболее удобной формулой для расчета коэффициент корреляции является следующая:

Коэффициент корреляции можно рассчитать и по другим формулам:

; .

Другим показателем тесноты связи между признаками является коэффициент детерминации – это квадрат коэффициента корреляции .

7. Множественный коэффициент корреляции характеризует интенсивность влияния на результативный признак нескольких факторов. Формула множественного коэффициента корреляции имеет вид:

,

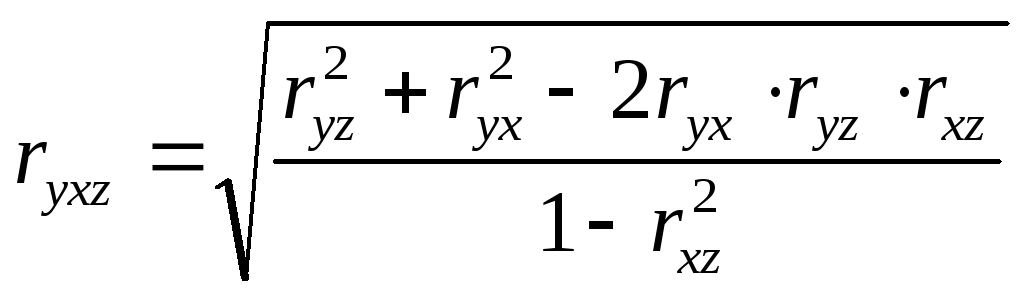где , , – парные коэффициент корреляции, которые определяются по соответсвующим формулам:

;

;

.

8. В случае нелинейной связи между результативным и факторным признаками рассчитывается эмпирическое корреляционное отношение по следующей формуле:

,

где – межгрупповая дисперсия;

– общая дисперсия.

Межгрупповая дисперсия определяется так:

,

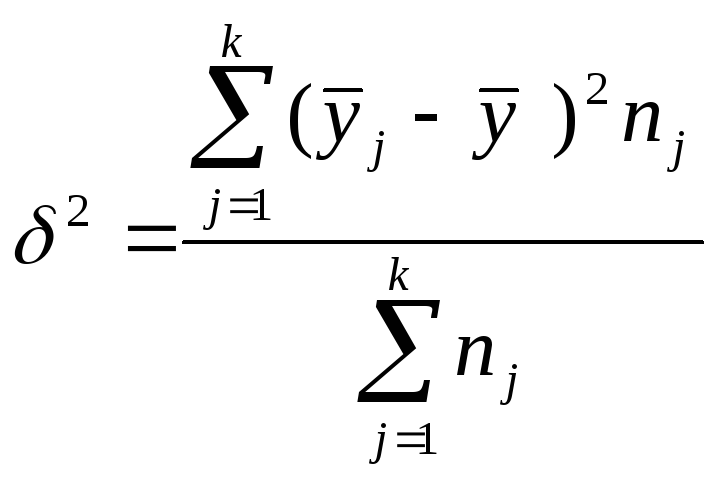где – средние значения результативного признака в соответствующих группах;

– общая средняя для всей совокупности;

– число наблюдений в соответствующей группе;

– число выделенных групп.

Общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий , которая определяется по формуле:

,

где – дисперсия результативного признака в соответствующей группе.