
- •2.Высказывания.Операции над высказываниями.
- •3. Тождественно истинные и тождественно ложные высказывания. Равносильные высказывания.
- •4.Суперпозиция функций. Бинарные отношения. Свойства бинарных отношений
- •5.Отношение порядка. Отношение эквивалентн. Бинарные опер.
- •6. Алгебры. Алгебра Кантора и булева алгебра. Изоморфизм. Операции над двоичными числами.
- •7. Булевы функции. Мощность множества булевых функций от переменных.
- •8. Элементарные булевы функции.
- •9. Формулы. Основные эквивалентности формул.
- •Порядок действий в формулах алгебры логики
- •10. Принцип двойственности. Двойственные булевы функции.
- •11.Теорема о разложении
- •12. Совершенные дизъюнктивные нормальные формы.
- •25. Перестановки с повторениями
- •26. Полиномиальная теорема. Принцип Дирихле.
- •27.Рекуррентные соотношения и производящие функции.
- •28. Принцип включения и исключения:
- •30. Схемы правильных рассуждений. Аксиоматические теории
- •32. Минимальные , кратчайшие и тупиковые днф.
- •33. Сокращённые днф. Построение сокращённых днф булевых функций методом Блейка.Пример.
- •34. Построение сокращённых днф булевых функций методом Квайна.Пример.
- •35.Построение Сокращенных днф геометрическим методом. Пример.
- •36. Построение минимальных днф с помощью карт Карно.
- •37. Метод Нельсона. (Построение сокращенной днф с помощью кнф).
- •38.Построение всех тупиковых днф. Алгоритм минимизации функций в классе нормальных форм.
- •39. Понятие о функциях k-значной логики. Их особенности.
- •40.Графы. Изоморфизм графов.
- •41.Способы задания графов.
- •42. Действия над графами.
- •43. Ориентированные и неориентированные графы.
- •44.Маршруты. Пути. Цепи. Связные графы.
- •45. Геометрическая реализации графа. Теорема о реализации конечного графа в трёхмерном пространстве.
- •46.Эйлеровы циклы. Задача о кенигсбергских мостах. Теорема Эйлера.
- •47.Обобщенная теорема об эйлеровых цепях.
- •48. Гамильтоновы графы. Задача о коммивояжере.
- •49. Взвешенный граф. Граф-дерево.
- •50. Цикломатическое число. Остов графа. Базис циклов.
- •51. Двудольные графы.
- •52. Планарные графы. Критерий планарности.
- •53. Теорема Куратовского-Понтрягина. Граф Петерсена.
- •54.Двухполюсные сети. Параллельно-последовательные сети. Поток в сети.
- •55.Теорема Форда-Фалкерсона о максимальном потоке. Расчет максимального потока в сети.
- •56.Общие принципы помехоустойчивого кодирования. Примеры.
- •57.Типы ошибок. Сжатие информации.
- •58.Код Хэмминга.
- •59.Троичный код Хэмминга. Пример.
- •60.Алфавитное кодирование.
- •61. Алгоритм Фано.Пример
- •62. Алгоритм кодирования Хаффмена.Пример
- •63. Формальные грамматики. Основные понятия.
- •64. Классификация языков по Хомскому
- •65. Типы языков. Вывод цепочек. Дерево вывода
- •66.Конечные автоматы. Автоматы Мили и Мура. Канонические уравнения
- •67.Таблица состояний, диаграмма состояний автомата.
- •68.Дешифратор.
- •69.Реализация автоматов схемами.
- •70. Ограниченно детерминированные функции. Информационные деревья.
- •71. Понятие алгоритма. Основные свойства алгоритмов. Вычислимость.
- •72. Рекурсивные функции. Операторы суперпозиции и примитивной рекурсии.
- •73. Примитивно рекурсивные предикаты. Свойства.
- •74. Классы рекурсивных функций. (п.Р., о.Р., ч.Р.). Тезис Черча.
- •75. Машины Тьюринга. Принципы работы. Протокол работы.
- •76.Машины Тьюринга. Примеры. Функции, вычислимые по Тьюрингу.
28. Принцип включения и исключения:
Теорема. Если А1, A2, ..., An – некоторые конечные множества, то:
m(A1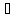 A2
A2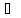 …
…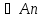 )=[m(A1)+…+m(An)]-[m(A1
)=[m(A1)+…+m(An)]-[m(A1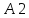 )+m(A1
)+m(A1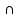 A3)+…+m(An-1
A3)+…+m(An-1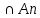 )]+[m(A1
)]+[m(A1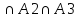 )+…+m(An-2
)+…+m(An-2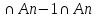 )]-…+(
)]-…+(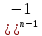 [m(A1
[m(A1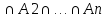 )].
)].
Поясним формулировку
этой теоремы. Правая часть формулы в
теореме представляет собой алгебраическую
сумму n слагаемых (взятых в квадратные
скобки), имеющих попеременно знак «+» и
«–».Первое слагаемое – число элементов,
входящих хотя бы в одно из множеств А1,
A2,
..., An,
второе – число элементов, входящих хотя
бы в одно из множеств
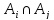 (i < j, i = 1, …,
n, j = 1, …, n), третье – число элементов,
входящих хотя бы в одно из множеств
(i < j, i = 1, …,
n, j = 1, …, n), третье – число элементов,
входящих хотя бы в одно из множеств
 (i < j < k, i = 1, …, n, j = 1, …, n, k = 1, …,
n) и так далее.
. Последнее
слагаемое, взятое со знаком
(i < j < k, i = 1, …, n, j = 1, …, n, k = 1, …,
n) и так далее.
. Последнее
слагаемое, взятое со знаком
 ,
– число элементов в множествеA1
,
– число элементов в множествеA1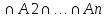 . Такое
попеременное включение и исключение
слагаемых с целью учета каждого элемента
только один раз и послужило причиной
для названия этой формулы: формула
включений и исключений.
. Такое
попеременное включение и исключение
слагаемых с целью учета каждого элемента
только один раз и послужило причиной
для названия этой формулы: формула
включений и исключений.
Эту формулу можно
доказать, используя метод математической
индукции. Мы ограничимся ее доказательством
только для случая n
= 3, то есть покажем, что m(AUBUC)=
m(A)+m(B)+m(C)-m(B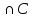 )-m(A
)-m(A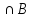 )-m(A
)-m(A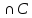 )+m(A
)+m(A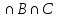 )
)
Доказательство. Чтобы не писать индексы, рассмотрим множества А, В, С. Используя очевидное равенство AU B UC = AU(B UC) и то, что эта формула доказана для двух множеств, получим:
m(AU B UC)
= m(AU[B UC]) = m(A) + m(B UC) − m(A [B UC]) ,
[B UC]) ,
Так
как
A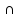 [B UC] = [A
[B UC] = [A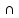 B]U[A
B]U[A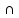 C]то:
C]то:
m(A)
+ m(B UC) − m(A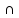 [B UC]) = m(A) + m(B UC) − m([A
[B UC]) = m(A) + m(B UC) − m([A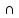 B]U[A
B]U[A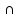 C])
,
C])
,
Применяя формулу включений и исключений для двух множеств еще два раза, получим:
m(A)
+ m(B UC) − m(A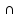 [B UC])=m(A)+m(B)+m(C)-m(B
[B UC])=m(A)+m(B)+m(C)-m(B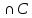 )-(m(A
)-(m(A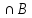 )+m(A
)+m(A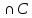 )-m[A
)-m[A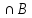 ]
]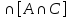 ).
).
После очевидных преобразований, получим в итоге доказываемую формулу
m(AUBUC)=
m(A)+m(B)+m(C)-m(B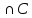 )-m(A
)-m(A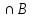 )-m(A
)-m(A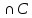 )++m(A
)++m(A
29.
30. Схемы правильных рассуждений. Аксиоматические теории
Формула, содержащая
булевы переменные называется тождественно
истинной или тавтологией, если она
выражает булеву функцию f(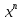 )
)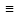 1.
Аналогичная формула называется
тождественно ложной, если эта формула
выражает булеву функцию f(
1.
Аналогичная формула называется
тождественно ложной, если эта формула
выражает булеву функцию f(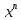 )
)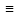 0.Формула
называется выполнимой, если f(
0.Формула
называется выполнимой, если f(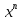 )
)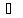 0.
Опровержима, если f(
0.
Опровержима, если f(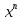 )
)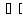 1.Перечислим
основные тавтологии:
1.Перечислим
основные тавтологии:
1)Av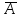 .
.
2)A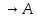 .
.
3)A (B
(B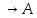 ).
).
4)(A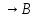 )
)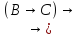 (A
(A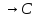 )).
)).
5)(A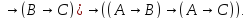
6)A&B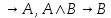 .
.
7)A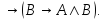
8)A ;
B
;
B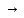 (A
(A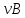 ).
).
9)(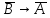 )
)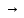 ((
((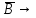 A)
A)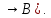
10)((A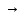 B)
B)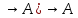 .
.
1)-10)-тавтологии, ABC-произвольная формула.
Рассуждение будем
считать правильным, если из конъюнкций
правильных посылок следует истинность
заключений. Пусть P1…Pn
посылки заключения Q
для правильности. Схемы рассуждений из
P1…Pn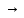 Q
необходимо установить, что формула
(P1&P2&…&Pn)
Q
необходимо установить, что формула
(P1&P2&…&Pn)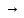 Q.
При этом правильным является лишь
рассуждения формулы Pi,Q
не обязательно должны быть истины. Если
какая либо из формул Pi=0,
то P1&…&Pn=0;
0
Q.
При этом правильным является лишь
рассуждения формулы Pi,Q
не обязательно должны быть истины. Если
какая либо из формул Pi=0,
то P1&…&Pn=0;
0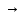 Q
всегда истина.
Q
всегда истина.
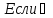 Pi=1,i=
Pi=1,i=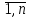 ;P1&…&Pn=1;1
;P1&…&Pn=1;1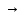 Q;
если Q=1;
Q;
если Q=1;
Опр: Формальной аксиоматической теорией T,будем называть систему состоящую из 1)некоторого алфавита А.Элементы которого аi будем называть символами теории слова ai,ai+1,…,ai+n. –выражения в Т.2)выделенные выражения в Т называются формулами теории. 3) В Т выделены подмножества формул называемые аксиомами.4) в теории Т определяется множества правил R1,…,Rk. k называется правилом вывода. Если А1…Аn, В-формулы и выполнены отношения R(A1,…,An,B),то формула B называется непосредственно следствием формулы A1,…,An подчиненные правилу R.
Выводом в Теории
называется любая последовательность
формулы B1,…Bn
такая что формула Bi
где i=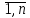 .
Являлась либо аксиомой теории Т либо
непосредственным следствием предыдущей
формулы этой последовательности.
.
Являлась либо аксиомой теории Т либо
непосредственным следствием предыдущей
формулы этой последовательности.
Формула С называется теоремой теории Т, если существует вывод последней формулы которой является С. Таким образом теорема в теории Т формула которой может быть выведена из аксиом теории по имеющимся правилам вывода. В общем случае множества формул {В1,…,Вn}=Г.
Пусть {A1,…,Am}
такая что Аi
либо аксиомы теории, Либо формулы
последовательности Г. Тогда формула Аm
называется следствием
системы формул
Г и обозначается Г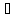 А:
А:
Основные правила вывода:
Пусть Г произвольное множество формул. АВС –некоторые формулы.
1)Г,
А
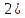 Г
Г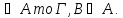
3)(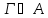 )&(Г
)&(Г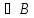 )&(АВ
)&(АВ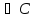 )
)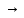 (Г
(Г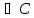 ).
).
4)
(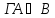 )&(
)&(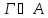 )
)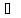 )&(Г
)&(Г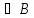 ).
).
31. Формула
содержащая булевые переменные называется
тождественно
истинной
или тавтологией,
если она выражает собой булевую функцию
f(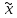 n)
n)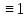 .
.
Аналогично, формула
тождественно
ложная, если
эта формула выражает функцию f(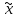 n)
n)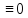 .
.
Формула называется
выполнимой, если f(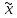 n)
n)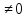 ;
опровержимой, если f(
;
опровержимой, если f(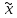 n)
n)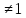 .
.
Перечислим основные тавтологии:
1) А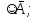
2) A→A;
3) A→(B→A);
4) (A→B)→((B→C)→(A→C));
5) (A→(B→C))→((A→B)→(A→C));
6) A&B→A , A&B→B;
7) A→(B→A&B);
8) A→(A˅B) , B→(A˅B);
9)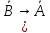 )→((
)→((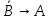 )→B);
)→B);
10)((A→B)→A)→A; (Закон Пирса) (A,B,C – произвольные формулы)
Предикативные формулы:
Предикатом будем называть ф-цию P:Mn→{0,1}, где M- И либо Л , где М – произвольное множество, т.е. ф-ция P сопоставляет каждому вектору ∀(m1,m2,…,mk) координату 0 или 1.
Множество M называется предметной областью предиката, m1,m2,…,mn предметными переменными , а P– предикатным символом n-местного предиката.
Предикатной
формулой
будем называть формулу содержащую
переменные символы предикатов, логические
символы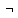 ,& , ˅ , ~ , → .
,& , ˅ , ~ , → .
P-символ предиката.
1) x1,…,xn–предикатные переменные, то P(x1,…,xn) –n-местный предикат и все его переменные свободны.
2) Если
A-предикатная
формула, то
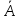 – так же предикатная формула с тем же
набором свободных переменных.
– так же предикатная формула с тем же
набором свободных переменных.
3) Если A,B– предикатные формулы и нет переменных свободных в одной формуле и связанных в друг., то формулы A&B, A˅B , A~B , A→B также формулы с теми же свободными и связанными переменными .
4) Если A – формула содержащая свободную переменную –x, то ∀x:A , ∃x:A так же предикатные формулы в каждой из которых х – связная переменная (количество свободных переменных уменьшилось на одну)
Эквивалентными будем называть те предикатные формулы, у которых области истинности совпадают.
Исчисление предикатов:
Теорема: (о подстановке) Пусть F-тождественно истинная формула, тогда подстановка на места её переменных x1 ,…, xn формул B1 ,…, Bn такая , что получаем правильных предикативная формула даёт общезначимую формулу логики предикатов.
Теорема: (Черча) Не существует алгоритма, который для любой формулы логики предикатов устанавливал бы, общезначимая формула либо нет.
Составим аксиоматическую теорию исчисления предикатов:
Алфавиты и предикатные формулы определим так же как они определялись для булевых функций.
 , →
, →
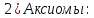 А1
-А4 –
совпадают
с соответствующими аксиомами исчисления
высказываний. А5
, ∀xi
(P(xi)→P(xk))
если P(xi)
не содержит переменной xk
A6
,
P(xi)→∃xk(P(xk))
А1
-А4 –
совпадают
с соответствующими аксиомами исчисления
высказываний. А5
, ∀xi
(P(xi)→P(xk))
если P(xi)
не содержит переменной xk
A6
,
P(xi)→∃xk(P(xk))
3)Правило вывода:
1)A,(A→B)/B ; (A,A→B⊦B)
2)B→A(xi)/B→∀xiA(xi) ;если B не содержит переменной xi
3) A(xi)→B/ ∃xi( A(xi))→B; при этом B не содержит xi
4)Любую связанную переменную в формуле А можно заменить в кванторе и во всех вхождениях этой переменной в области действия этого квантора.
Понятия вывода теоремы вывода из системы гипотез определяется так же как в ∀ аксиом теории.
Аксиомы исчисления предикатов общезначимые формулы
Формула полученная из общезначимой по любому из правил вывода 1-4 так же является общезначимой
Любая выводимая в исчислении предикатов формула является общезначимой
Исчисления
предикатов не противоречивы, т.к.
невозможно одновременно вывести формулы
Aи
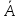 .
.
