
- •2.Высказывания.Операции над высказываниями.
- •3. Тождественно истинные и тождественно ложные высказывания. Равносильные высказывания.
- •4.Суперпозиция функций. Бинарные отношения. Свойства бинарных отношений
- •5.Отношение порядка. Отношение эквивалентн. Бинарные опер.
- •6. Алгебры. Алгебра Кантора и булева алгебра. Изоморфизм. Операции над двоичными числами.
- •7. Булевы функции. Мощность множества булевых функций от переменных.
- •8. Элементарные булевы функции.
- •9. Формулы. Основные эквивалентности формул.
- •Порядок действий в формулах алгебры логики
- •10. Принцип двойственности. Двойственные булевы функции.
- •11.Теорема о разложении
- •12. Совершенные дизъюнктивные нормальные формы.
- •25. Перестановки с повторениями
- •26. Полиномиальная теорема. Принцип Дирихле.
- •27.Рекуррентные соотношения и производящие функции.
- •28. Принцип включения и исключения:
- •30. Схемы правильных рассуждений. Аксиоматические теории
- •32. Минимальные , кратчайшие и тупиковые днф.
- •33. Сокращённые днф. Построение сокращённых днф булевых функций методом Блейка.Пример.
- •34. Построение сокращённых днф булевых функций методом Квайна.Пример.
- •35.Построение Сокращенных днф геометрическим методом. Пример.
- •36. Построение минимальных днф с помощью карт Карно.
- •37. Метод Нельсона. (Построение сокращенной днф с помощью кнф).
- •38.Построение всех тупиковых днф. Алгоритм минимизации функций в классе нормальных форм.
- •39. Понятие о функциях k-значной логики. Их особенности.
- •40.Графы. Изоморфизм графов.
- •41.Способы задания графов.
- •42. Действия над графами.
- •43. Ориентированные и неориентированные графы.
- •44.Маршруты. Пути. Цепи. Связные графы.
- •45. Геометрическая реализации графа. Теорема о реализации конечного графа в трёхмерном пространстве.
- •46.Эйлеровы циклы. Задача о кенигсбергских мостах. Теорема Эйлера.
- •47.Обобщенная теорема об эйлеровых цепях.
- •48. Гамильтоновы графы. Задача о коммивояжере.
- •49. Взвешенный граф. Граф-дерево.
- •50. Цикломатическое число. Остов графа. Базис циклов.
- •51. Двудольные графы.
- •52. Планарные графы. Критерий планарности.
- •53. Теорема Куратовского-Понтрягина. Граф Петерсена.
- •54.Двухполюсные сети. Параллельно-последовательные сети. Поток в сети.
- •55.Теорема Форда-Фалкерсона о максимальном потоке. Расчет максимального потока в сети.
- •56.Общие принципы помехоустойчивого кодирования. Примеры.
- •57.Типы ошибок. Сжатие информации.
- •58.Код Хэмминга.
- •59.Троичный код Хэмминга. Пример.
- •60.Алфавитное кодирование.
- •61. Алгоритм Фано.Пример
- •62. Алгоритм кодирования Хаффмена.Пример
- •63. Формальные грамматики. Основные понятия.
- •64. Классификация языков по Хомскому
- •65. Типы языков. Вывод цепочек. Дерево вывода
- •66.Конечные автоматы. Автоматы Мили и Мура. Канонические уравнения
- •67.Таблица состояний, диаграмма состояний автомата.
- •68.Дешифратор.
- •69.Реализация автоматов схемами.
- •70. Ограниченно детерминированные функции. Информационные деревья.
- •71. Понятие алгоритма. Основные свойства алгоритмов. Вычислимость.
- •72. Рекурсивные функции. Операторы суперпозиции и примитивной рекурсии.
- •73. Примитивно рекурсивные предикаты. Свойства.
- •74. Классы рекурсивных функций. (п.Р., о.Р., ч.Р.). Тезис Черча.
- •75. Машины Тьюринга. Принципы работы. Протокол работы.
- •76.Машины Тьюринга. Примеры. Функции, вычислимые по Тьюрингу.
25. Перестановки с повторениями
Пусть задано
конечное множество U={a1,a2,…,an}.
Рассмотрим набор из элементов ai1,ai2,…,aik
где ai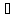 U,
i
U,
i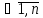 ,
k≤n
этот набор называется выборкой объемов
к из n
элементов.
,
k≤n
этот набор называется выборкой объемов
к из n
элементов.
Выборка называется
упорядоченной, если в ней задан порядок
следование элементов, если порядка
следования не существует, то выборка
называется неупорядоченной. Упорядоченные
выборки n
из n
называется
перестановкой. Число таких перестановок
Pn=n!
Упорядочен выборки объем m
из n
элементов(m<n)
где все элементы различны называется
размещениями и обозначается
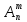 ,
число таких размещений
,
число таких размещений
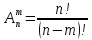 .
.
Перестановка с повторениями : пусть имеется n элементов среди которых , к1 элементов 1 типа , к2 элементов 2 типа … кr элемент r типа. Причем к1+к2+…+ кr=n упорядочен выборки из таких m элементов по n называется перестановкой с повторением и обозначается
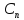 (k1,k2,…,kr)
=
(k1,k2,…,kr)
=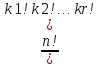 ,
их называют полиниальными коэффициентами.
,
их называют полиниальными коэффициентами.
26. Полиномиальная теорема. Принцип Дирихле.
Принцип Дирихле
: Если в m
ящиках расположены n
кроликов, при этом (n>m)
то хотя бы в 1 из ящиков будет находиться
больше чем 1 кролик . (Например :9 ящиков
, 10 кроликов.) Если n
кроликов рассажены в m
ящиках, то хотя бы в 1 ящике находится
не менее
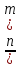 кроликов, а также хотя бы в 1 ящике не
более
кроликов, а также хотя бы в 1 ящике не
более
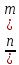 кроликов.
кроликов.
Полиномиальная
теорема: Выражение
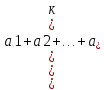 равно сумме всех возможных слагаемых
вида
равно сумме всех возможных слагаемых
вида
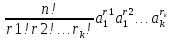 ,
гдеr1+r2+…+
,
гдеr1+r2+…+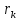 =n,
то
=n,
то
есть
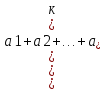 =
=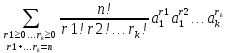 .
.
Доказательство: Перемножим последовательность
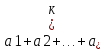 n
раз. Тогда получаем
n
раз. Тогда получаем
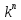
слагаемых вида
d1…dn,
где каждый множитель di
равен или а1, или а2 ,…, или
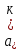 .Обозначим
.Обозначим
через В(r1,…,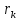 )
совокупность всех слагаемых ,
)
совокупность всех слагаемых ,
где а1 встречается множителем r1 раз ,а2-r2 раз ,
…,
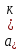 -
-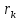 раз .Число таких слагаемых равно
раз .Число таких слагаемых равно
Cn(
r1,…,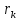 ).
НоCn(
r1,…,
).
НоCn(
r1,…,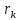 )=
)=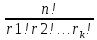 .
.
Следовательно
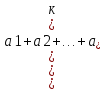 =
=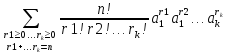 .
.
27.Рекуррентные соотношения и производящие функции.
Рекуррентные соотношения :это соответствия позволяющие свести решение комбинаторной задачи для некоторого числа объектов к аналогичной задаче с меньшей размерностью.
Пусть f(n)
некоторое рекуррентное соотношение и
для него известно
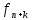 =F(
=F(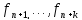 )(1).
ГдеF(y1,…,yk)
известная функция от k
переменных тогда (1) называется рекуррентным
соотношением к –ого порядка.
Последовательность чисел
)(1).
ГдеF(y1,…,yk)
известная функция от k
переменных тогда (1) называется рекуррентным
соотношением к –ого порядка.
Последовательность чисел
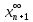 называется решением соотношения (1),
если при подстановке
называется решением соотношения (1),
если при подстановке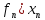 в (1) получается верное равенство.
в (1) получается верное равенство.
Если в (1) первые к соотношений f1,f2,…fk заданы произвольно то соотношение (1) имеет бесконечное число соотношений.
Опр:
Пусть f(n)
общее решение соотношения (1) если оно
зависит от к произвольных постоянных
то записывают
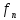 =
=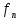 (С1,С2…Сn,n).
Если для любого Xn
существует С1’,С2’…Ск’
что
(С1,С2…Сn,n).
Если для любого Xn
существует С1’,С2’…Ск’
что
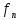 является решением то записываютXn=
является решением то записываютXn=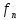 (С1’,С2’…Ск’,n).
(С1’,С2’…Ск’,n).
Опр:
Линейное однородное рекуррентное
соотношение 2-го порядка с постоянными
коэффициентами называется рекуррентным
соотношением вида
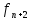 =
=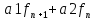 ,n=1,2…(2)
,n=1,2…(2)
Уравнение
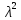 =а1
=а1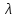 +а2
(3) называется характеристическим
уравнением
соотношения (2).
+а2
(3) называется характеристическим
уравнением
соотношения (2).
Теор:
Если характеристическое уравнение (3)
имеет 2 различных корня
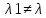 2
то общее решение рекуррентного соотношения
(2) имеет вид,
2
то общее решение рекуррентного соотношения
(2) имеет вид,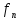 =С
=С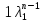 +С2
+С2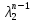 .
Если уравнение (3) имеет кратные корни
то общее решение имеет вид
.
Если уравнение (3) имеет кратные корни
то общее решение имеет вид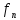 =(С1+С2)
=(С1+С2)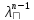 .
.
Опр:
Линейное рекуррентное соотношение к-го
порядка называется соотношение вида
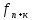 =а1
=а1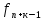 +а2
+а2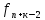 +…+
+…+
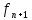 +
+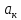
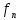 (4).
(4).
Характеристическим
для (4) будет уравнение вида
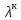 =а1
=а1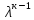 +а2
+а2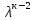 +…+
+…+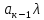 +
+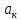 .(5)
.(5)
Теор:
1)Пусть
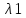 ,…,
,…,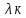 Попарно различные корни характеристического
уравнения (5) Тогда общее уравнение (4)
записывается в виде
Попарно различные корни характеристического
уравнения (5) Тогда общее уравнение (4)
записывается в виде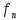 =С
=С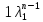 +С2
+С2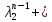 …+
Сn
…+
Сn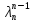
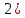 Пусть
Пусть
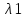 ,…,
,…,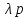 попарно различны корни характеристического
уравнения (5) имеющие кратностьmi
причем m1+m2+…+mp=k,
i=1,p.
Тогда общее решение уравнения (4) имеет
вид
попарно различны корни характеристического
уравнения (5) имеющие кратностьmi
причем m1+m2+…+mp=k,
i=1,p.
Тогда общее решение уравнения (4) имеет
вид
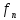 =(С11+С12n+…+
=(С11+С12n+…+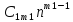 )
)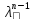 +…+(Cp1+Cp2+…
+…+(Cp1+Cp2+…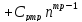 )
)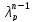 .
Для решения рекуррентных соотношений
используют так же метод производящих
функций.
.
Для решения рекуррентных соотношений
используют так же метод производящих
функций.
Пусть задано
линейное рекуррентное соотношение
а0=0,
а1=1,
аn=5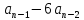 ,n>=2.
,n>=2.
Производящую
функцию G(z)будем
искать в виде ряда
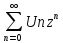 =a0+a1z+a2
=a0+a1z+a2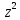 +…
с этой целью отношениеG
умножают соответственно на
+…
с этой целью отношениеG
умножают соответственно на
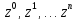 …. 0
…. 0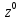 +1
+1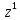 +…+(5
+…+(5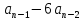 )
)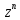 +…+a0+a1z+
+…+a0+a1z+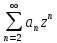 =z+5
=z+5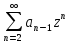 -6
-6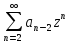 G(z)=z+5zG(z)-6
G(z)=z+5zG(z)-6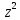 G(z).
Откуда производящая функция G(z)=
G(z).
Откуда производящая функция G(z)=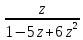 .
Оно задает производящую функцию
последовательности (5) в замкнутом виде
.
Оно задает производящую функцию
последовательности (5) в замкнутом виде
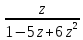 =
=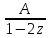 +
+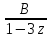 .An=
.An=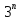 -
-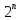 ,n=0,1,2…
решение рекурсивного выражения 5.
,n=0,1,2…
решение рекурсивного выражения 5.
