
- •2.Высказывания.Операции над высказываниями.
- •3. Тождественно истинные и тождественно ложные высказывания. Равносильные высказывания.
- •4.Суперпозиция функций. Бинарные отношения. Свойства бинарных отношений
- •5.Отношение порядка. Отношение эквивалентн. Бинарные опер.
- •6. Алгебры. Алгебра Кантора и булева алгебра. Изоморфизм. Операции над двоичными числами.
- •7. Булевы функции. Мощность множества булевых функций от переменных.
- •8. Элементарные булевы функции.
- •9. Формулы. Основные эквивалентности формул.
- •Порядок действий в формулах алгебры логики
- •10. Принцип двойственности. Двойственные булевы функции.
- •11.Теорема о разложении
- •12. Совершенные дизъюнктивные нормальные формы.
- •25. Перестановки с повторениями
- •26. Полиномиальная теорема. Принцип Дирихле.
- •27.Рекуррентные соотношения и производящие функции.
- •28. Принцип включения и исключения:
- •30. Схемы правильных рассуждений. Аксиоматические теории
- •32. Минимальные , кратчайшие и тупиковые днф.
- •33. Сокращённые днф. Построение сокращённых днф булевых функций методом Блейка.Пример.
- •34. Построение сокращённых днф булевых функций методом Квайна.Пример.
- •35.Построение Сокращенных днф геометрическим методом. Пример.
- •36. Построение минимальных днф с помощью карт Карно.
- •37. Метод Нельсона. (Построение сокращенной днф с помощью кнф).
- •38.Построение всех тупиковых днф. Алгоритм минимизации функций в классе нормальных форм.
- •39. Понятие о функциях k-значной логики. Их особенности.
- •40.Графы. Изоморфизм графов.
- •41.Способы задания графов.
- •42. Действия над графами.
- •43. Ориентированные и неориентированные графы.
- •44.Маршруты. Пути. Цепи. Связные графы.
- •45. Геометрическая реализации графа. Теорема о реализации конечного графа в трёхмерном пространстве.
- •46.Эйлеровы циклы. Задача о кенигсбергских мостах. Теорема Эйлера.
- •47.Обобщенная теорема об эйлеровых цепях.
- •48. Гамильтоновы графы. Задача о коммивояжере.
- •49. Взвешенный граф. Граф-дерево.
- •50. Цикломатическое число. Остов графа. Базис циклов.
- •51. Двудольные графы.
- •52. Планарные графы. Критерий планарности.
- •53. Теорема Куратовского-Понтрягина. Граф Петерсена.
- •54.Двухполюсные сети. Параллельно-последовательные сети. Поток в сети.
- •55.Теорема Форда-Фалкерсона о максимальном потоке. Расчет максимального потока в сети.
- •56.Общие принципы помехоустойчивого кодирования. Примеры.
- •57.Типы ошибок. Сжатие информации.
- •58.Код Хэмминга.
- •59.Троичный код Хэмминга. Пример.
- •60.Алфавитное кодирование.
- •61. Алгоритм Фано.Пример
- •62. Алгоритм кодирования Хаффмена.Пример
- •63. Формальные грамматики. Основные понятия.
- •64. Классификация языков по Хомскому
- •65. Типы языков. Вывод цепочек. Дерево вывода
- •66.Конечные автоматы. Автоматы Мили и Мура. Канонические уравнения
- •67.Таблица состояний, диаграмма состояний автомата.
- •68.Дешифратор.
- •69.Реализация автоматов схемами.
- •70. Ограниченно детерминированные функции. Информационные деревья.
- •71. Понятие алгоритма. Основные свойства алгоритмов. Вычислимость.
- •72. Рекурсивные функции. Операторы суперпозиции и примитивной рекурсии.
- •73. Примитивно рекурсивные предикаты. Свойства.
- •74. Классы рекурсивных функций. (п.Р., о.Р., ч.Р.). Тезис Черча.
- •75. Машины Тьюринга. Принципы работы. Протокол работы.
- •76.Машины Тьюринга. Примеры. Функции, вычислимые по Тьюрингу.
76.Машины Тьюринга. Примеры. Функции, вычислимые по Тьюрингу.
Машиной Тьюринга Т называется тройка множеств T= <A, Q, P>, где: A=A(T)={a0, a1,…, am} – внешний алфавит машины Т (обычно a0=0, a1=1) Q=Q(T)={q0, q1,…,qm} – алфавит внутренних состояний или внутренний алфавит машины Т.
Р = РТ = {T(i,j)
| i=1,…,n;
j=0,1,…,m}
– программа машины Т; где Т(i,j)
– команды этой программы, причем, для
каждой пары (i,j)
существует одна единственная команда
Т(i,j),
которая имеет один из видов: qiaj
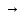 qkal
qiaj
qkal
qiaj
 qkR
qkR
qiaj
 qkL
qkL
пример: рассмотрим МТ :
Т: q1а
 qbR,
q1b
qbR,
q1b
 q2
aR,
q2а
q2
aR,
q2а
 q0,
q2b
q0,
q2b
 q1L
A={a,b}
q1L
A={a,b}
Рассмотрим работу МТ над конфигурациями
1) q1aa
… 0 0 q1а 0 …
… 0 b a q2 0 …
… 0 b a q0 0 …
T(a,a)=ba (T: aa|- ba)
2) q1 ab
… 0 a q1b 0 …
… 0 b bq1 0 …
… 0 bq1 b 0 …
… 0 a bq2 0 …
… 0 a q1b 0 …
T не применимо к слову ab
МТ Т можно задавать при помощи таблицы переходов и диаграммы переходов.
В таблице переходов строки соответственно внутренние состояниям qi считывающего устройства, столбец символом внешнего алфавита. В клетках таблицы правые части соответствующих команд.
Например: Пусть А={0 1 a b c} c –вспомогательный символ q10P(a,b)|- q001n0, P(a,b)-слово длины n
q10 -> q5R q20 -> q31L q4a -> 0L
q21 -> R q31 -> L q4b -> 0L
q2a -> R q3a -> L q4c -> 0L
q2b -> R q3b -> L q50 -> q3L
q3 -> q0 q3c -> q5R q51 -> q4L
q40 -> R q41 -> q0L q5a -> q2R
q5b -> R
|
|
0 |
1 |
a |
b |
c |
|
q1 |
q5R |
|
|
|
|
|
q4 |
q31L |
R |
R |
R |
|
|
q3 |
q0 |
L |
L |
L |
q5R |
|
q4 |
R |
q0L |
0L |
0L |
0L |
|
q5 |
q3L |
q4L |
q2R |
R |
|
