49. Взвешенный граф. Граф-дерево.

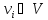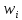Определим понятие взвешенного графа. Сопоставим каждой вершиневесиз множества весов W . В результате получим множество взвешенных вершин{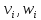}, при этом не обязательно, чтобы все веса были различными.

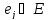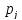Аналогично сопоставим каждому ребрувесиз множества весовP. В результате получим множество взвешенных ребер {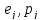}. Определенные выше множества взвешенных вершин и ребер определяют в совокупности граф, взвешенный по вершинам и ребрам.

Опр. Н-граф называется неориентированным деревом (или просто деревом), если он связен и не содержит циклов, а значит, петель и кратных ребер. Дерево – это минимальный связный граф в том смысле, что при удалении хотя бы одного ребра он теряет связность.

Наличие этих двух свойств (связность и отсутствие циклов) позволяет жестко связать число вершин и число ребер: в дереве с n вершинами всегда n -1 ребер. В этом графе 8 вершин и 7 ребер. Ни одно ребро нельзя удалить из графа без того, чтобы он не потерял связность.

Деревом называется связный граф без циклов. Вот пример дерева (рис1):

А вот пример графа, не являющегося деревом (рис 2):

Рис 2. Рис1.

50. Цикломатическое число. Остов графа. Базис циклов.

Пусть – связный граф. Остов(наименьший из всех графов, имеющий n вершин) этого графа содержит n-1 ребро.

Если ранее в графе было N ребер, то удалить пришлось k=N-n+1 ребро. Величина k=N-n+1 называется цикломатическим числом связного графа.

Цикломатическое число несвязного графа равно сумме цикломатических чисел связных компонент. Очевидно, что для любого графа–дерева это число равно нулю.

Пусть G — произвольный (n, m)-граф с k компонентами связности. Если G — не дерево, то в нем (его компонентах связности) существуют циклы. Рассмотрим какой-либо цикл и удалим из него некоторое ребро. При этом количество компонент связности не увеличится. Если после этого еще останутся циклы, то рассмотрим следующий из них и снова удалим какое-либо его ребро. Продолжим этот процесс до тех пор, пока не исчезнут все циклы. Полученный в результате подграф, который, очевидно, является лесом и имеет столько же компонент связности, как и исходный граф G, называется остовом графа G.

Базис циклов— базис пространства циклов графа, состоящий только из простых циклов. Базис циклов является максимальным набором независимых простых циклов графа или минимальным набором простых циклов, от которых зависят все циклы.

51. Двудольные графы.

Опр. Граф G называется двудольным (или четным), если

множество его вершин V распадается на два непересекающихся подмножества 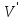и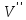, таких, что каждое ребро графа G имеет один конец из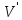, а другой из.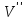

Для двудольных графов справедлива следующая теорема: граф Gявляется двудольным, если все его циклы имеют четную длину.

Опр. Граф называется двудольным, если множество его вершин можно разбить на две части (доли) так, чтобы концы каждого ребра принадлежали разным долям.   Пример

Определение

Двудольный граф называется полным двудольным, если любые две его вершины, принадлежащие разным долям, смежны. Обозначают: – полный двудольный граф, где в одной долеn, а в другой доле m вершин. Пример