
- •2.Высказывания.Операции над высказываниями.
- •3. Тождественно истинные и тождественно ложные высказывания. Равносильные высказывания.
- •4.Суперпозиция функций. Бинарные отношения. Свойства бинарных отношений
- •5.Отношение порядка. Отношение эквивалентн. Бинарные опер.
- •6. Алгебры. Алгебра Кантора и булева алгебра. Изоморфизм. Операции над двоичными числами.
- •7. Булевы функции. Мощность множества булевых функций от переменных.
- •8. Элементарные булевы функции.
- •9. Формулы. Основные эквивалентности формул.
- •Порядок действий в формулах алгебры логики
- •10. Принцип двойственности. Двойственные булевы функции.
- •11.Теорема о разложении
- •12. Совершенные дизъюнктивные нормальные формы.
- •25. Перестановки с повторениями
- •26. Полиномиальная теорема. Принцип Дирихле.
- •27.Рекуррентные соотношения и производящие функции.
- •28. Принцип включения и исключения:
- •30. Схемы правильных рассуждений. Аксиоматические теории
- •32. Минимальные , кратчайшие и тупиковые днф.
- •33. Сокращённые днф. Построение сокращённых днф булевых функций методом Блейка.Пример.
- •34. Построение сокращённых днф булевых функций методом Квайна.Пример.
- •35.Построение Сокращенных днф геометрическим методом. Пример.
- •36. Построение минимальных днф с помощью карт Карно.
- •37. Метод Нельсона. (Построение сокращенной днф с помощью кнф).
- •38.Построение всех тупиковых днф. Алгоритм минимизации функций в классе нормальных форм.
- •39. Понятие о функциях k-значной логики. Их особенности.
- •40.Графы. Изоморфизм графов.
- •41.Способы задания графов.
- •42. Действия над графами.
- •43. Ориентированные и неориентированные графы.
- •44.Маршруты. Пути. Цепи. Связные графы.
- •45. Геометрическая реализации графа. Теорема о реализации конечного графа в трёхмерном пространстве.
- •46.Эйлеровы циклы. Задача о кенигсбергских мостах. Теорема Эйлера.
- •47.Обобщенная теорема об эйлеровых цепях.
- •48. Гамильтоновы графы. Задача о коммивояжере.
- •49. Взвешенный граф. Граф-дерево.
- •50. Цикломатическое число. Остов графа. Базис циклов.
- •51. Двудольные графы.
- •52. Планарные графы. Критерий планарности.
- •53. Теорема Куратовского-Понтрягина. Граф Петерсена.
- •54.Двухполюсные сети. Параллельно-последовательные сети. Поток в сети.
- •55.Теорема Форда-Фалкерсона о максимальном потоке. Расчет максимального потока в сети.
- •56.Общие принципы помехоустойчивого кодирования. Примеры.
- •57.Типы ошибок. Сжатие информации.
- •58.Код Хэмминга.
- •59.Троичный код Хэмминга. Пример.
- •60.Алфавитное кодирование.
- •61. Алгоритм Фано.Пример
- •62. Алгоритм кодирования Хаффмена.Пример
- •63. Формальные грамматики. Основные понятия.
- •64. Классификация языков по Хомскому
- •65. Типы языков. Вывод цепочек. Дерево вывода
- •66.Конечные автоматы. Автоматы Мили и Мура. Канонические уравнения
- •67.Таблица состояний, диаграмма состояний автомата.
- •68.Дешифратор.
- •69.Реализация автоматов схемами.
- •70. Ограниченно детерминированные функции. Информационные деревья.
- •71. Понятие алгоритма. Основные свойства алгоритмов. Вычислимость.
- •72. Рекурсивные функции. Операторы суперпозиции и примитивной рекурсии.
- •73. Примитивно рекурсивные предикаты. Свойства.
- •74. Классы рекурсивных функций. (п.Р., о.Р., ч.Р.). Тезис Черча.
- •75. Машины Тьюринга. Принципы работы. Протокол работы.
- •76.Машины Тьюринга. Примеры. Функции, вычислимые по Тьюрингу.
44.Маршруты. Пути. Цепи. Связные графы.
Пусть
G
– н-граф. Маршрутом
М графа G
называется такая последовательность
ребер (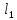 ,
,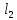 ,
… ,
,
… ,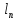 ),
в которой два ребра
),
в которой два ребра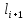 ,
,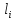 имеют общую вершину. В маршруте одно и
то же ребро может встречаться несколько
раз. Начало маршрута
имеют общую вершину. В маршруте одно и
то же ребро может встречаться несколько
раз. Начало маршрута .
.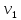 инцидентно
инцидентно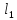 .
.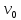 не инцидентно
не инцидентно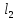 .
.
Маршрут, начало и конец которого совпадают называется циклическим.
Маршрут, в котором все ребра разные – цепь. Цепь, не имеющая повторяющихся вершин, называется простой цепью. Циклический маршрут, являющийся цепью, называется циклом, являющийся простой цепью – простым циклом.
Вершины
 ,
,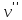 называютсясвязанными,
если существует маршрут М с началом в
называютсясвязанными,
если существует маршрут М с началом в
 и концом в
и концом в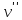 .
.
Связанные маршрутом вершины, связаны также и простой цепью. Причем отношение связности обладает свойством эквивалентности и определяет разбиение множества V(G) на не пересекаемые множества V:(G) связных вершин. Граф G называется связным, если все его вершины связаны между собой. Если граф G несвязный, то связными будут множества V:(G), которые называются связными компонентами графа. Каждый н-граф распадается единственным образом на прямую сумму своих связных компонентов.
Пример.

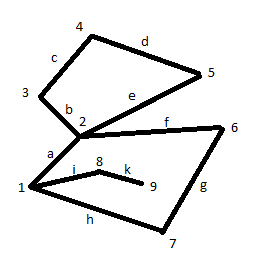
Пусть G – орграф.
Последовательность
дуг, в которой конец предыдущей дуги
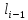 совпадает с началом следующей дуги,
называетсяпутем.
Одна и та же дуга в пути может встречаться
несколько раз. Путь называется
ориентированной
цепью, если
каждая дуга встречается не больше одного
раза; простой
цепью – если
не содержит повтор вершин. Замкнутый
путь называется контуром.
Контур называется циклом,
если путь является цепью; простым
циклом –
если простой цепью. Граф называется
связным,
если он связан без учета ориентации
дуг, и сильно
связным,
если из любой вершины графа в любую
другую существует путь. Число дуг пути
называется его длиной.
совпадает с началом следующей дуги,
называетсяпутем.
Одна и та же дуга в пути может встречаться
несколько раз. Путь называется
ориентированной
цепью, если
каждая дуга встречается не больше одного
раза; простой
цепью – если
не содержит повтор вершин. Замкнутый
путь называется контуром.
Контур называется циклом,
если путь является цепью; простым
циклом –
если простой цепью. Граф называется
связным,
если он связан без учета ориентации
дуг, и сильно
связным,
если из любой вершины графа в любую
другую существует путь. Число дуг пути
называется его длиной.
Определение. Путь называется простым, если все вершины графа, по которым он проходит, различны (более одного раза не проходит по одной вершине).
Определение. Путь называется замкнутым, если он начинается и заканчивается в одной и той же вершине (v0 = vn).
Определение. Циклом называется замкнутый путь, не проходящий более одного раза по одному и тому же ребру.
Определение. Цикл называется простым, если он более одного раза не проходит через одну и ту же вершину, то есть v0, …, vn-1 – различные.
45. Геометрическая реализации графа. Теорема о реализации конечного графа в трёхмерном пространстве.
Определение. Пусть задан некоторый неориентированный граф G = (V, E). Пусть любой вершине vi графа G сопоставлена некоторая точка ai: vi → ai, ai ≠ aj (i ≠ j), а любому ребру e = (a, b) сопоставлена некоторая непрерывная кривая L, соединяющая точки ai и aj и не проходящая через другие точки ak (k ≠ i, j). Тогда если все кривые, сопоставленные рёбрам, не имеют общих точек, кроме концевых, то говорят, что задана геометрическая реализация графа G.

Теорема. Для любого графа существует его реализация в трёхмерном пространстве.
Доказательство. Возьмём в пространстве любую прямую l и разместим на ней все вершины графа G. Пусть в G имеется q рёбер. Проведём связку из q различных полуплоскостей через l. После этого каждое ребро графа G можно изобразить линией в своей полуплоскости и они, очевидно, не будут пересекаться. Теорема доказана.
