
- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
17.Мат.Ожидание и его свойства.
Из всех характеристик случайных величин важнейшей является математическое ожидание СВ.
ОПР1:математическим
ожиданием дискретной СВ называется
величина рассчитываемая по формуле: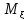 =
=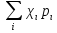
ОПР2:
математическим ожиданием непрерывной
СВ называется величина рассчитываемая
по формуле: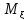 =
=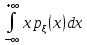
Математическое
ожидание характеризует среднее значение
СВ(среднее взвешенное по
вероятностям).Физический смысл
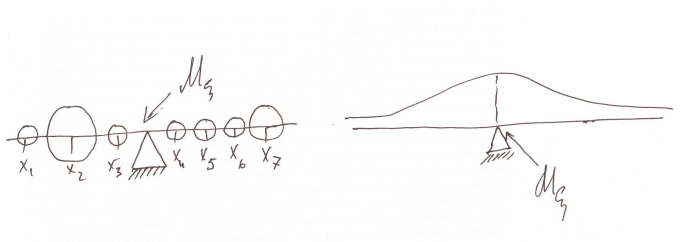
мат.ожидания:если на невесомом стержне
разместить единичную массу, поместив
в точке
 массу
массу для дискретного распределения или
размеров(единичную массу с плотностью
для дискретного распределения или
размеров(единичную массу с плотностью (x))для
непрерывного распределения, то
мат.ожидание будет координатой центра
тяжести
(x))для
непрерывного распределения, то
мат.ожидание будет координатой центра
тяжести
Свойства мат.ожиданий:
1.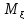 =C=const
=C=const
2.M(C)=C=const(мат.ожидание от постоянной величины = величине самой постоянной)
3.M(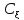 )=C
)=C ,где
C=const
,где
C=const
4.Если
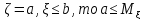 ≤b
≤b
5.СВ
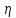 =f(
=f(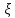 ),гдеf-некоторая функция ,то
),гдеf-некоторая функция ,то
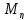 =
=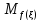 =
=

6.Для
любых СВ
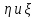 ,M(
,M(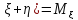 +
+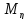 -это
свойство может быть обобщено на случай
трех и более величин,если их число
конечно.
-это
свойство может быть обобщено на случай
трех и более величин,если их число
конечно.
7.если
 независимые
СВ ,то
независимые
СВ ,то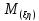 =
=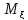 *
*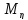 ,это
может быть обобщено на случай трех и
болеевеличин,если их число конечно.
,это
может быть обобщено на случай трех и
болеевеличин,если их число конечно.
18.Дисперсия и её свойства
Дисперсией
СВ
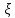 называется
число
называется
число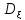 =M
=M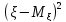
Дисперсия
это мера «разброса или рассеивания»
распределения СВ
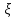 вокруг мат.ожидания .Дисперсия равна
моменту инерции распределения единичной
массы на прямой.
вокруг мат.ожидания .Дисперсия равна
моменту инерции распределения единичной
массы на прямой.
Рассмотрим
: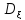 =M
=M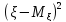 =M
=M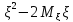 +
+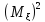 )=
)=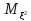 -2
-2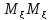 +
+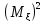 -
Упрощенная формула для обозначения
дисперсии
-
Упрощенная формула для обозначения
дисперсии
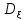 =
=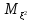 -
-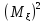
Свойства дисперсии :
Основные свойства дисперсии:
дисперсия любой случайной величины неотрицательна, Dx0;
дисперсия константы равна нулю, Dc=0;
для произвольной константы D(cx) =c2D(x);
дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x±h) =D(x) +D(h).
1.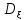 =const≥0
=const≥0
2.D(C)=0,c=const
// D(C)=M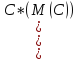 =M
=M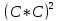 =M(0)=0
=M(0)=0
3.D(C*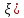 =
=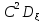 // D(C*
// D(C*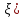 =M
=M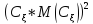 =M
=M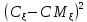 =M(C(
=M(C( ))=
))=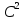 M
M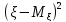 =
=
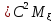
4.Если
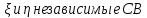 ,то
дисперсия суммы :D(
,то
дисперсия суммы :D( )=M
)=M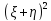 -
-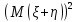 =
=
M(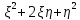 )-(
)-(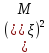 +2
+2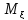
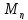 +
+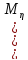 )=
)=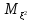 +2
+2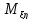 +
+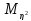 -
-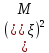 -2
-2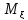
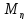 -
-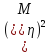 =
=
=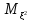 -
-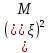 +
+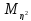 -
-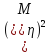 =
=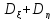 ,т.к.
,т.к.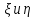 независимы,то
2
независимы,то
2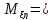 2
2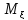
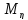
5.Дисперсия суммы конечного числа попарно независимых СВ = сумме их дисперсий
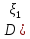 +
+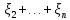 )=
)=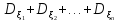
из
формулы
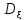 =M
=M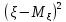 следует ,что если
следует ,что если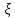 измеряется в метрах ,например,
измеряется в метрах ,например,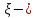 уровень
воды в реке ,то
уровень
воды в реке ,то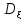 будет измерятся в
будет измерятся в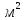 .Чтобы
привести характеристику рассеивания
измерения к единицам измерения СВ
.Чтобы
привести характеристику рассеивания
измерения к единицам измерения СВ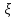 нужно извлечь из дисперсии корень
квадратный.
нужно извлечь из дисперсии корень
квадратный.
ОПР1:средним
квадратичным отклонением СВ
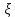 называется величина
называется величина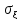 =+
=+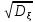
Формулы для вычисления дисперсии:
1)если
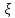 -дискретная
СВ ,то по формуле
-дискретная
СВ ,то по формуле
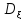 =M
=M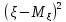 :
:
(1)
 =
=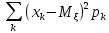
(2)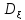 =
=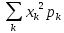 -
-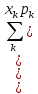
Если
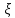 –непрерывная
СВ ,то по определению по формуле
–непрерывная
СВ ,то по определению по формуле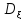 =M
=M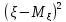
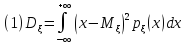
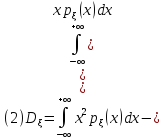
ДСВ:
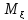 =
=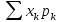
ИСВ
:
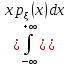
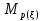 =
=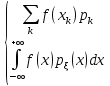
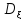 =M
=M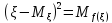 ,
f(x)=
,
f(x)=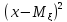 ,
,
 =
=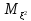 -
-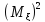 ,
,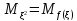 ,f(x)=
,f(x)=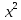
20 Числовые характеристики системы двух случайных величин.Ковариация.
ОПР1:Начальным моментом порядкаkСВ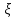 называется величина
называется величина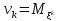
ОПР2:центральным моментом порядкаkназывается величина равная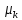 =M
=M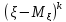
Очевидно
,что
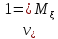 ,
, =M
=M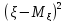 =
=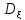 ,
,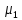 =M
=M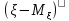 =
=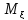 -
-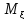 =0
=0
ОПР3:ковариацией
СВ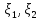 называется величина
называется величина
cov(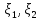 )=M
)=M =
=
=M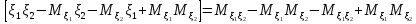 =
=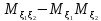
-произведени
Mмат.ожидания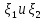 минус
произведения мат.ожиданий .
минус
произведения мат.ожиданий .
Свойства ковариаций :
cov(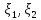 )=
)=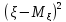 =
=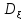
cov(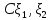 )=
Сcov(
)=
Сcov(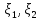 )
)
cov(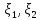 )=
cov(
)=
cov(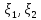 )
)
если
СВ
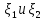 независимы ,то ковариацияcov(
независимы ,то ковариацияcov(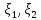 )=0.Пусть
)=0.Пусть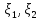 независимы,тогда
по формуле
независимы,тогда
по формуле
cov(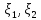 )=
)=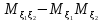 \\(т.к.
для независимых СВ
\\(т.к.
для независимых СВ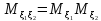 )\\
)\\
=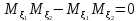 .
.
Т.о.
ковариация характеризует зависимость
случайных величин ,если cov(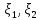 )≠0,то
СВ зависимы ,если жеcov(
)≠0,то
СВ зависимы ,если жеcov(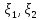 )=0,то
СВ могут быть как зависимы так и не
зависимыми.
)=0,то
СВ могут быть как зависимы так и не
зависимыми.
|cov(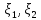 )|≤
)|≤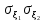
Т.о.
ковариация характеризует зависимость
СВ ,однако она не является безразмерной
«характеристикой зависимости»,если
,например
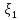 -температура
воздуха, а
-температура
воздуха, а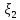 -влажность воздуха ,тоcov(
-влажность воздуха ,тоcov(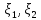 )
измеряется в градусах Цельсия ,умноженный
на проценты (
)
измеряется в градусах Цельсия ,умноженный
на проценты (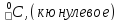 )иначе
говоря при умножении одной из СВ
)иначе
говоря при умножении одной из СВ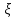 на константуCпо свойству
2 ковариация также умножается на это
число ,поэтому ,если
на константуCпо свойству
2 ковариация также умножается на это
число ,поэтому ,если
cov(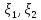 )=5,аcov(
)=5,аcov(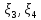 )=100,то
мы не можем сделать вывод ,что между
)=100,то
мы не можем сделать вывод ,что между зависимость больше ,чем между (
зависимость больше ,чем между (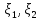 ).Чтобы
получить безразмерно характеристику
зависимости вводят новую числовую
характеристику.
).Чтобы
получить безразмерно характеристику
зависимости вводят новую числовую
характеристику.
