27.Стационарные случайные процессы(сп)

Определение 1:СП ξ(t) называется стационарным в узком смысле или строго стационарным,если его конечная функция распределения инвариантна отнасительно сдвигов всех моментов времени на одну и ту же величину τ.F(x₁,t₁;x₂,t₂;…;x_n,t_n)<F(x₁,t₁+ τ; x₂,t₂+ τ;…;x_n,t_n+ τ)(1)n=1,2,3,…Другими словами вероятносные свойства стационарного СП не зависят от начала наблюдений.

При n=1 условие стационарности дает F(x₁,t₁)= F(x₁,t₁+ τ) =>p(x₁,t₁)=p( x₁,t₁+ τ).Подогая τ=-t₁ получим,что F(x₁,t₁)= F(x₁), p(x₁,t₁)= p(x₁) т.е.одномерное распределение стационарного процесса не зависит от времени.А адномерное распределение определяет среднее значение и дисперсии СП,следовательно для строго стационарного СП среднее и дисперсия не зависят от времени:m_ξ(t)=m_ξ=const,Д_ξ(t)=Д_ξ=const

При n=2 из условия стационарности (1) следует,что F(x₁,t₁;x₂,t₂₎₌ F(x₁,t₁+ τ; x₂,t₂+ τ).Тоже самое справедливо для плотности распределения вероятностей пологая τ=-t₁ получим,что F(x₁,t₁;x₂,t₂₎₌ F(x₁,; x₂,t₂-t₁),т.е. двумерное распределение строго стационарное СП зависит от разности маментов времени t₂-t₁.С помощью двумерного распределения коррядяционная функция СП,эначит она для стационарного зависит лишь от разности моментов времени,т.е.одного аргумента: F_ξ(t₁,t₂)= F_ξ(t₂-t₁)

Определение 2:СП назовем стационарным в широком смысле,если его среднее значение и дисперсия не зависят от времени, коррядяционная функция зависит лишь от разности моментов времени.

28.Предмет мат. Статистики

Мат. статистика занимается занимается изучением методов сбора и обработки опытных данных для получения научных и прак. выводов.Мат.статистика(МС)-является разделом математики,очень близким к теории вероятности(ТВ),но МС решает задачи в некотором смысле противоположные задачам ТВ,при этом пользуясь теорией и методами ТВ.Например,в ТВ решалась след.задача:Задана нормальная случайная величина с плотностью распределения вероятностей

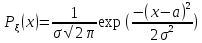.Тогда можно решать задачи о вычислении мат.ожидания данной СВ,дисперсии или вероятности попадания в интервал (α,р),но при этом параметры а и σ² считаются известными.Задичи МС в некотором смысле прямо противоположны этим задачам:в статистике рассматриваются данные некоторых опытов или наблюдений,тоесть известны значения,которые в результате опытов изучаемая СВ.И по этим статистическим данным можно получить свединия о параметрах,характеристиках распределения СВ или о характере самих распределений.Наример,можно поставить задачу о праверке гипотезы,что изучаемая СВ имеет нормальное распределение,или найти оценки неизвестных параметров а и σ².В МС обьектом исследования являются _{nданныя} эксперемента.

Вариационные ряды и их графическое изображение

Установление статистических закономерностей,присущих случайным явлениям основано на изучении статистических данных.Стат.данныя-свединья о том,какие значения принял в результате наблюдения интересующий нас признак или СВξ.Генеральной совакупностью называется совокупность обьектов или категория людей,все элементы которой подлежат изучению при статистическом анализе.Пусть исследуется успеваемость студентов 2-го курса вузов Беларуси.Тогда ген.совакупностью будут все студенты 2-го курса вузов Беларуси.На практике изучения всего набора элементов генер.совакупности оказывается затрудительным,поэтому изучают лишь часть этой совакупности.

Выборачной совакупностью или выборкой Х называют часть обьектов генеральной совакупности использумаего для исследования т.е Х={х₁,х₂,…,х_n}.При этом отдельные значения х_i называются элементами выборки или вариантами.Число Обьектов в выборке называют обьектом выборки о бозночаются обычно n.Например,если при исследовании успеваемости студентов отобраны 2000 студентов,то n=2000

Вариационным рядом называют совакупность вариантов упорядоченности по возрастанию значений.Рассмотрим часто используемыя методы предстовления стат.данных:Дискретным вариационным рядом называют таблицу,которая в 1-й строке содержит все значения(неповторяющиеся)изучаемого признака,упорядоченные по возрастанию,а во второй строке числа их повторений: n₁+n₂+n₃+…+n_s=n

Х	х1	х2	х3	…	хs
n	n1	n2	n3	…	ns

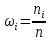Число n_i-частота элемента х_i,а отношениеназ. Относительной частатой.Дискретный вариационный ряд как правило используется при изучении дискретных СВ.При изучении непрерывных признаков пользуются интервальным вариационным рядом.Так же использование интервальных рядов целесообразно при изучении выборок большого обьема.

Интервал I=[x₁,x_n]разбивают на S промежутков одинаковой длины .При этом считают

что,каждый из промежутков содержит свой левый конец,но лишь последний промежуток содержит и свой правый конец.Для каждого из промежутка I_i подсчитывают число элементов выборки,попавших в него,результат представляют в виде таблицы:

Х	[x1,x2]	[x2,x3]	…	[xs,xs+1]
n	n1	n2	…	ns

Число интервалов определяется по формуле: S=1+3,322 lg n,n-число выборки тогда величина частичного интервала: =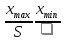.Для графического изображения вариационных рядов используется полигон и гистограмма.Полигон-ломаная,отрезки которой последовательно соединяют точки с координатами(х_i,n_i)((x_i,n_i/n)),i=1,S.Как правило полигон служит для изображения вариационного ряда.При построении полигона для интервального ряда в качестве х_i используют середины интервалов.Гистограмма-ступенчатая фигура из прямоугольников с основаниями,равными интервалу I_i=[x_i,x_i+1] и высотами равными плотности частоты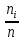.Сумарная площадь всех прямоугольников гистограммы равна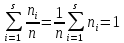.Гистограмма используется для предстовления интервальных вариационных рядов.Гистограмма является статистическим аналогом кривой плотности распределения вероятностейp_ξ(x).Эмпирической функцией распределения называется функция F_n(x)=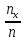,где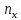-накопленая частота,равная числу выриантов меньших,чем х;n-число выборки. Эмпирическая функция распределения F_n(x) является статист. аналогом теоретической функции распределения F_ξ(x)генеральной совакупности.Функция F_n(x) обладает всеми свойствами распределения:

1. 0≤ F_n(x)≤1

2. F_n(x)-неубывающая функция

3. F_n(x)=0,при х≤х_min; F_n(x)=1, при х≥х_max

Эмпирическая функция распределения служит для оценки вида теоритической функции распределения случайного признака,полигон и гистограмма-для оценки вида теоритической плотности распределения.