Тема 1. Неопределенный интеграл

Вопросы для повторения:

1. Определение первообразнойи неопределенного интеграла.

2. Основные свойства неопределенного интеграла.

3. Таблица основных неопределенных интегралов.

Пример 1. Используя таблицу, найти следующие интегралы:

1. ;

2. ;

3. ;

4. ;

5. .

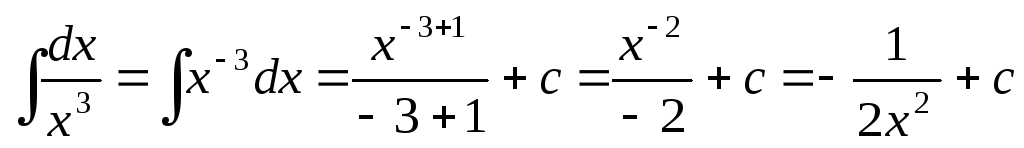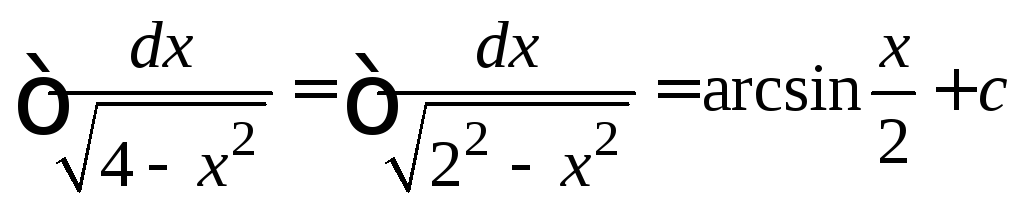Пример 2. Используя таблицу и основные свойства неопределенного интеграла, найти интегралы:

1. ;

2. 

3. ;

4. .

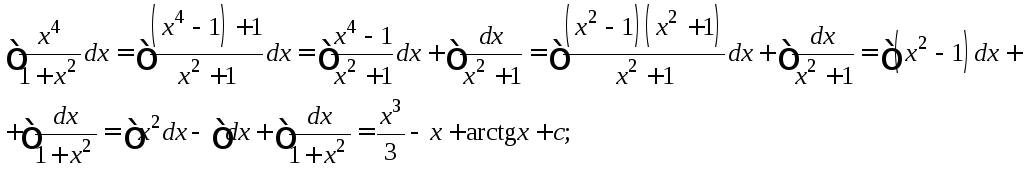
При сведении данного интеграла к табличному используется операция “подведения под знак дифференциала”:

,а– число,

, k ≠ 0,

,

,

,

,

.

Пример 3. Найти “почти табличные интегралы”:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

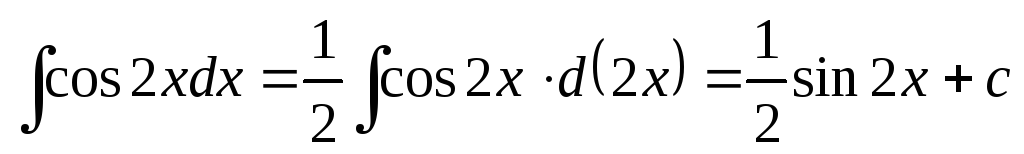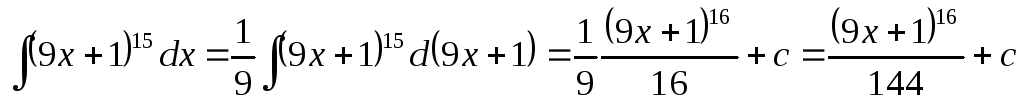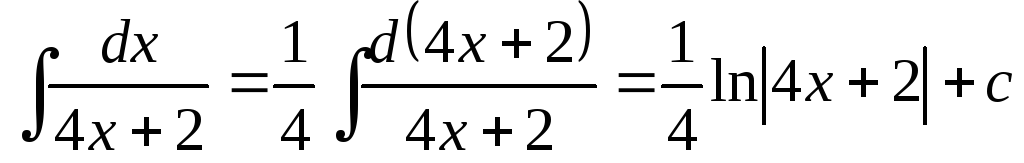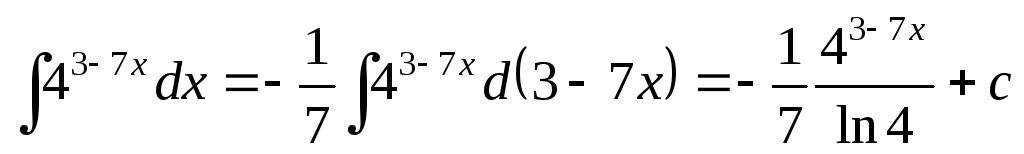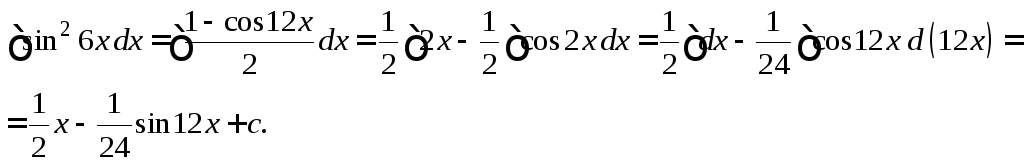Пример 4. Найти интегралы, используя подходящую подстановку:

1. 

Пусть х ² + 1 =t, тогда

.

2. 

Пусть , тогдаx = t²–1, dx=2t dt, тогда

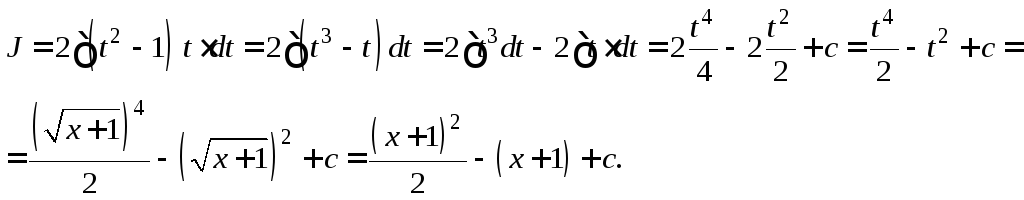
3) . Пустье^х = t, тогда х = ln t, .

Следовательно,

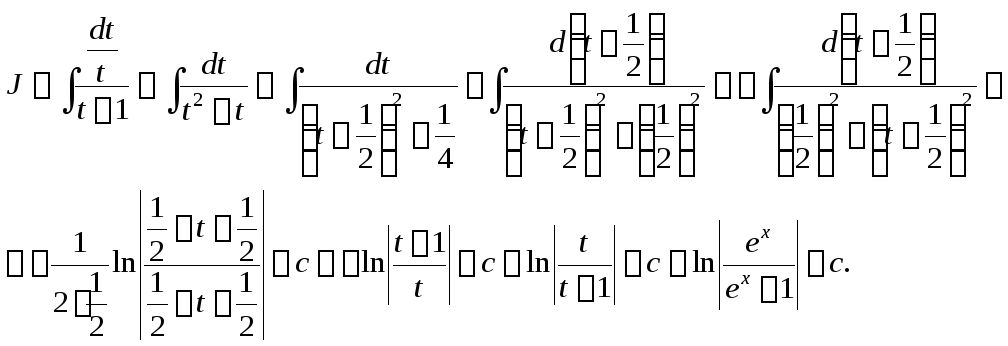
Пример 5. Найти интегралы, используя метод интегрирования по частям:

1. ;

2. 

3. 

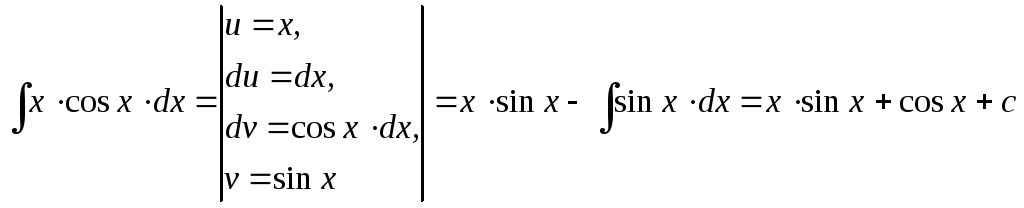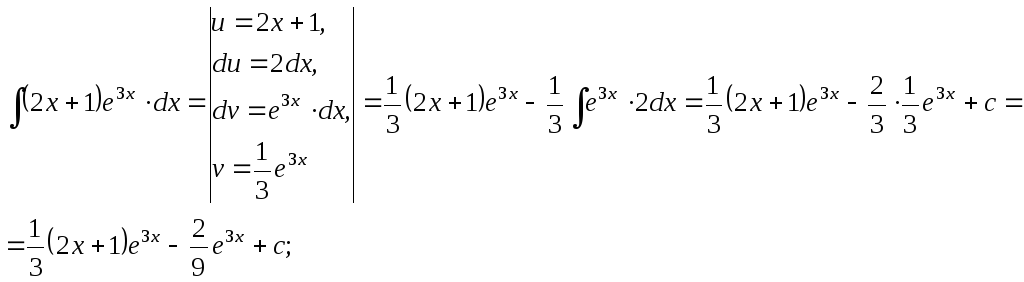
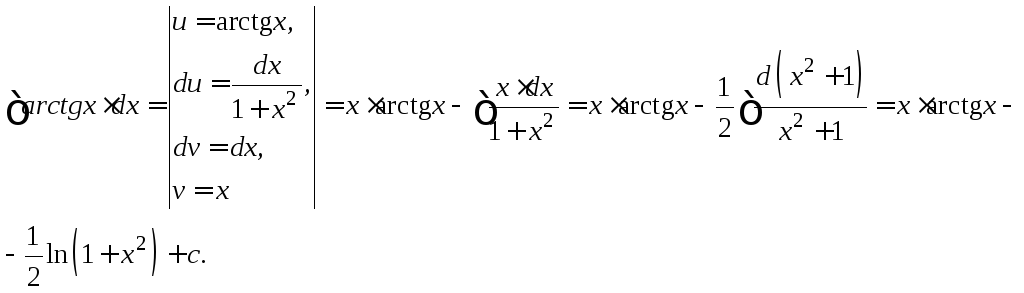
Задания для самостоятельного решения

1. Найти интегралы:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

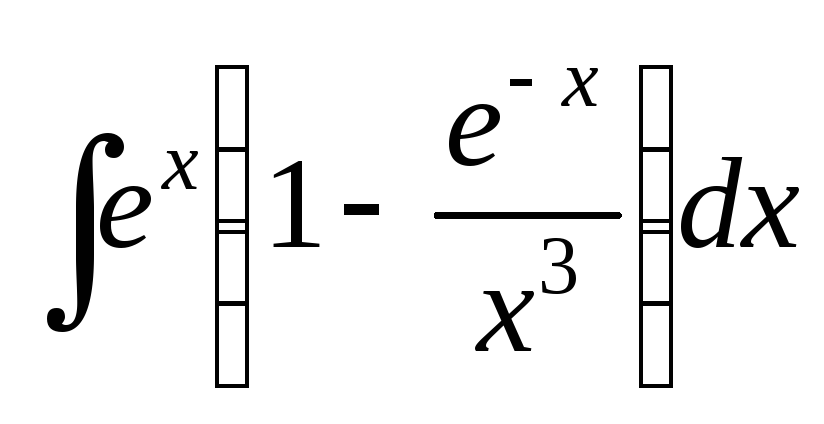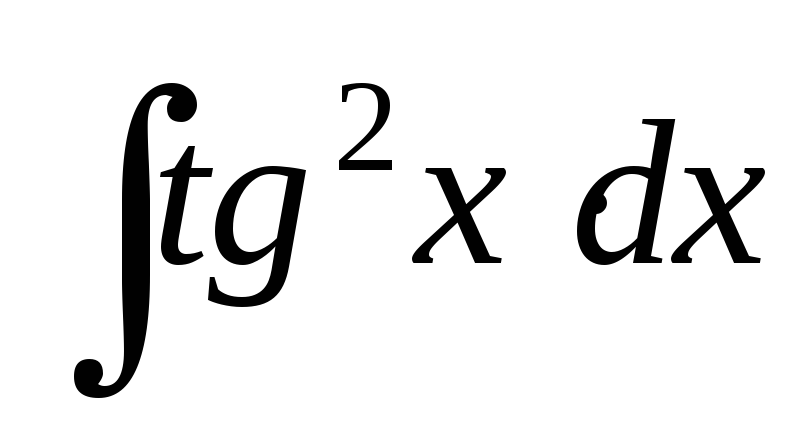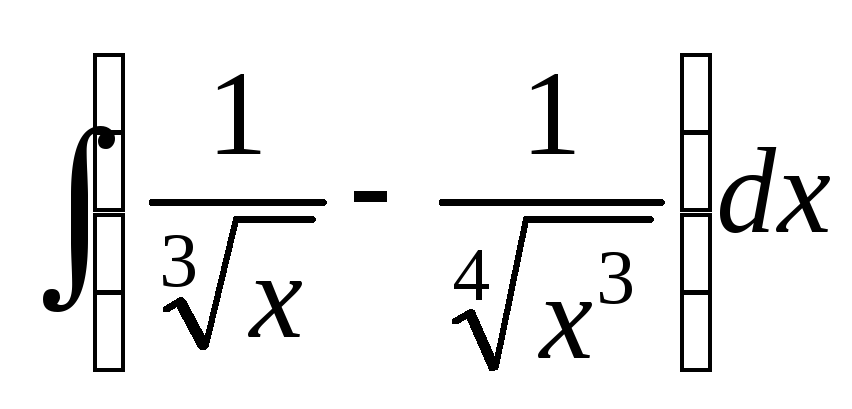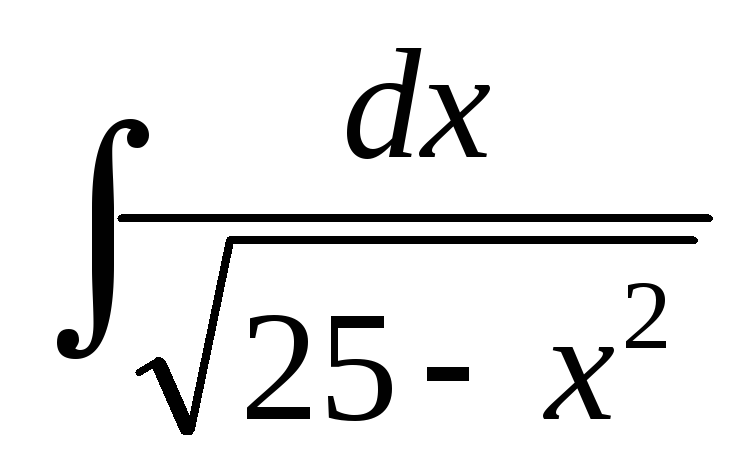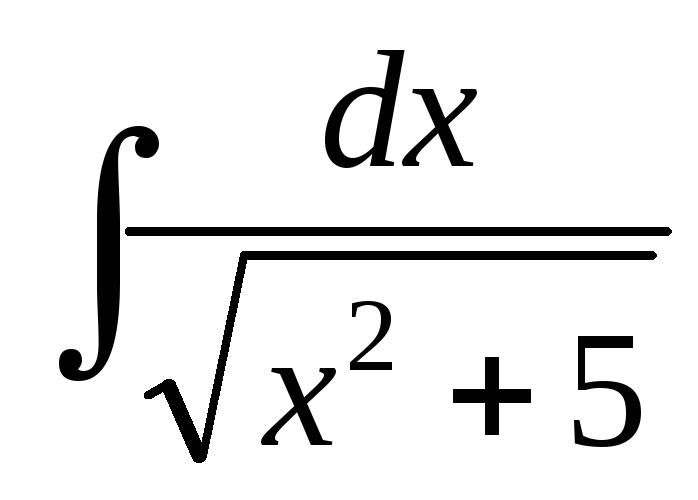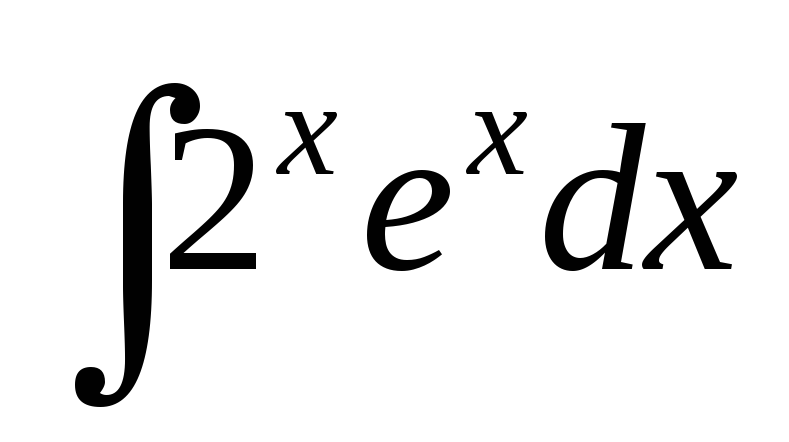4. Найти“почти табличные интегралы”:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. .

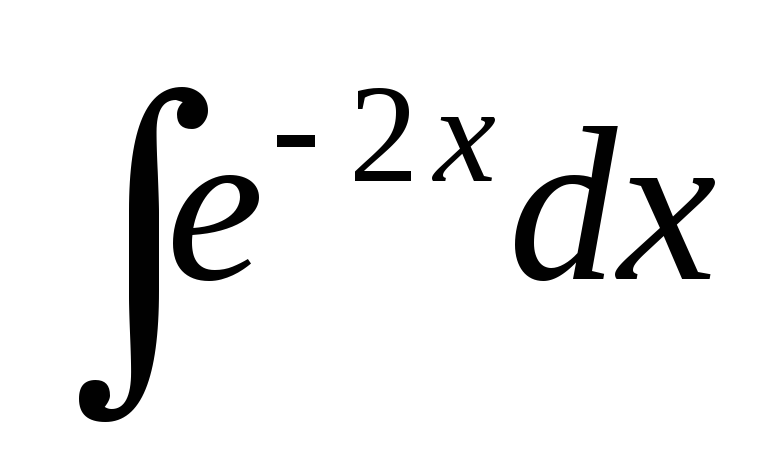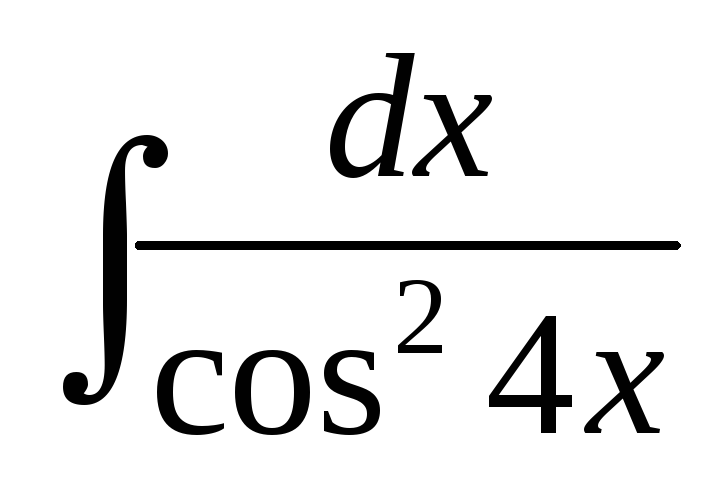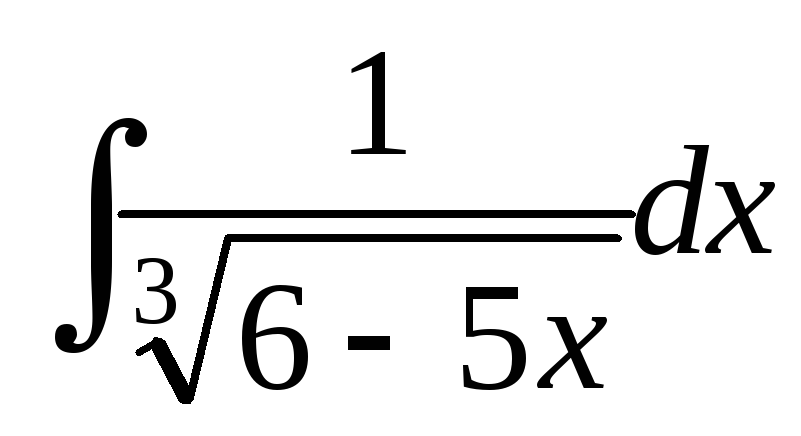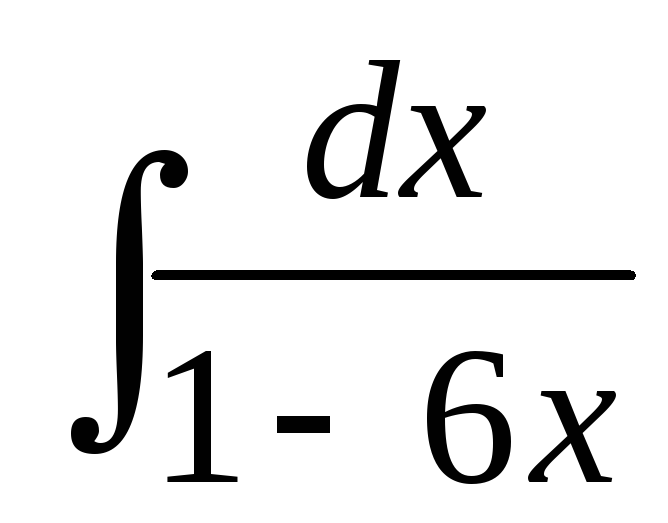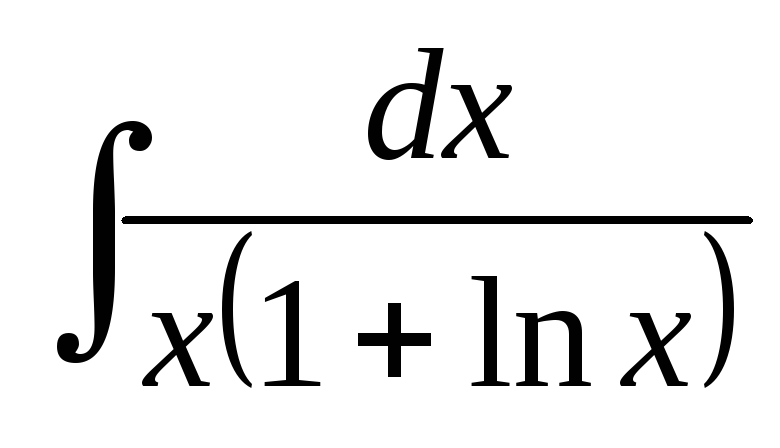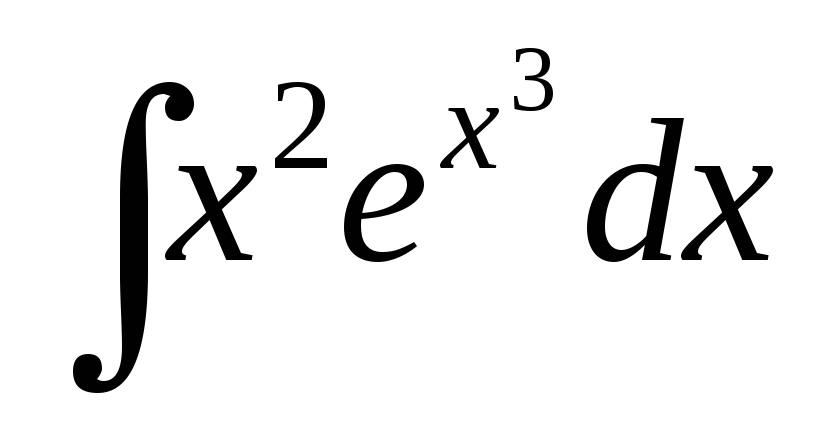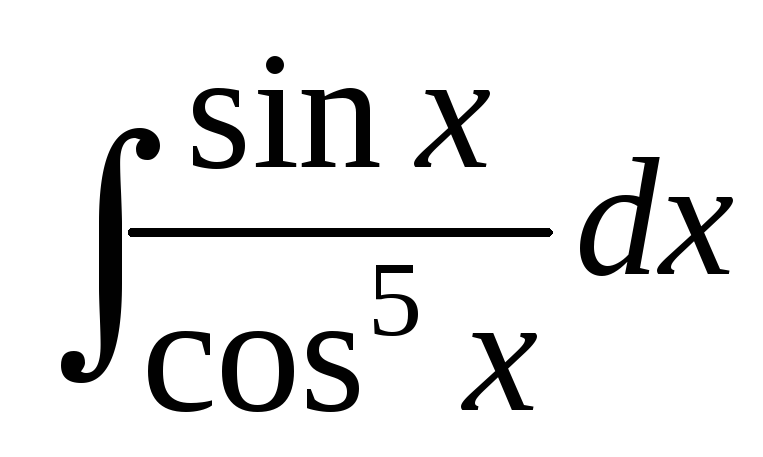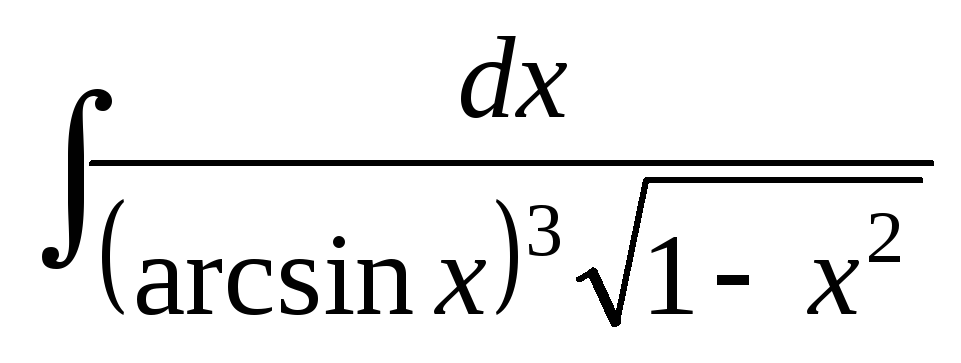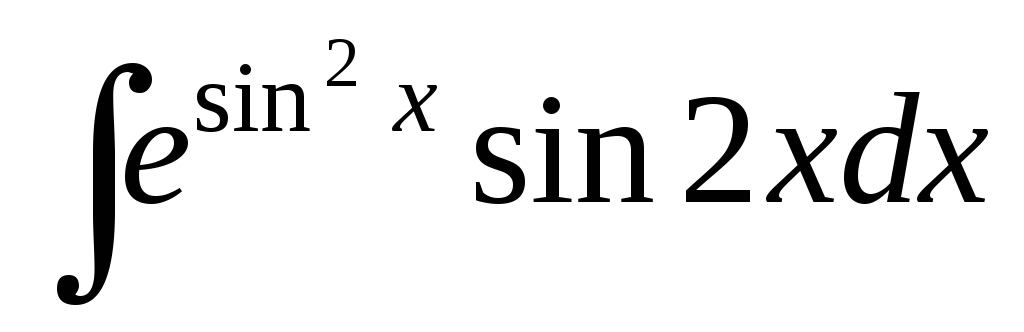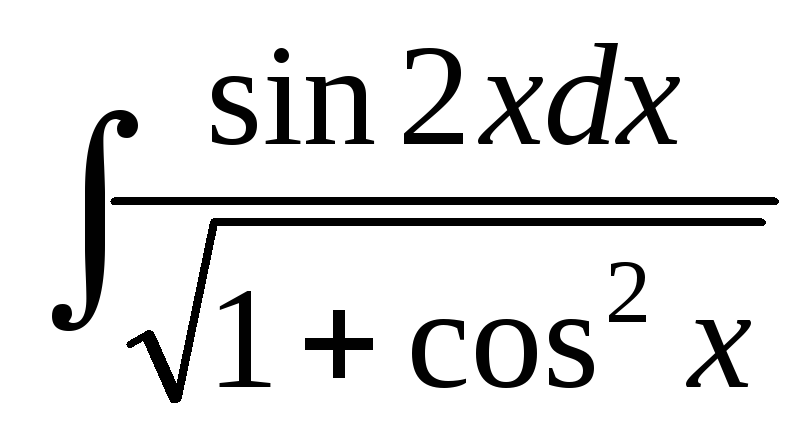5. Найти интегралы методом замены переменной:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. .

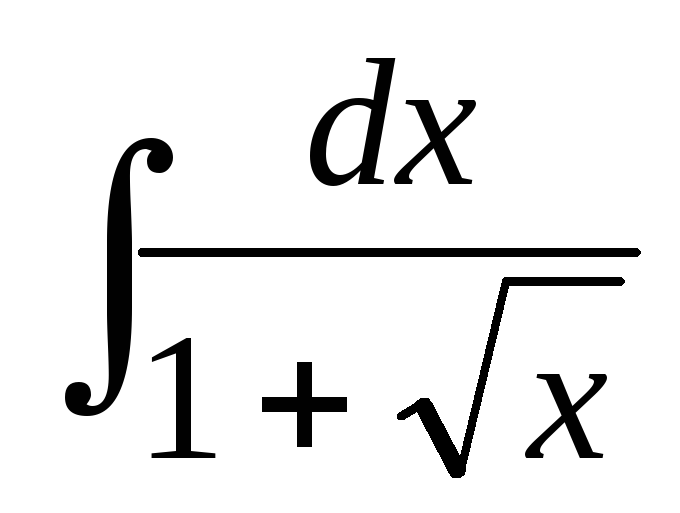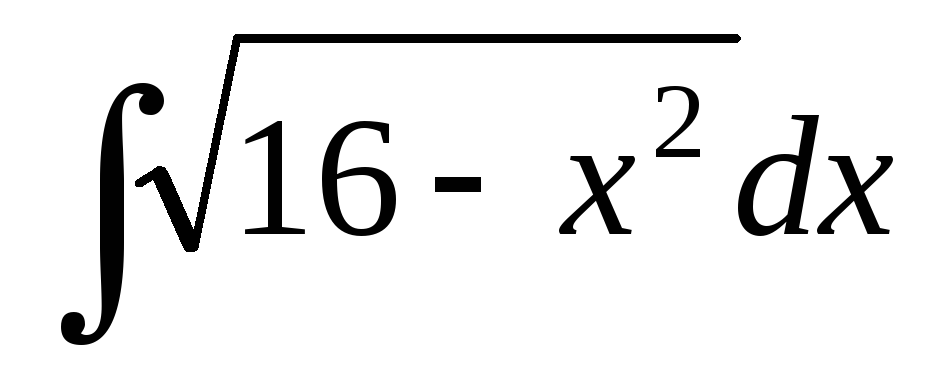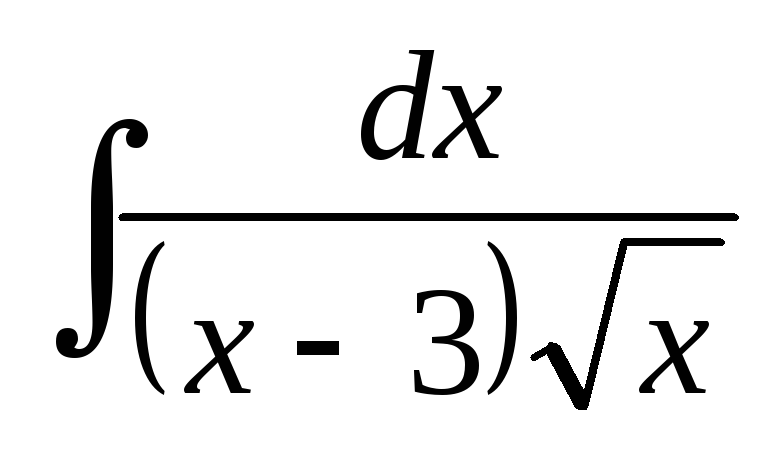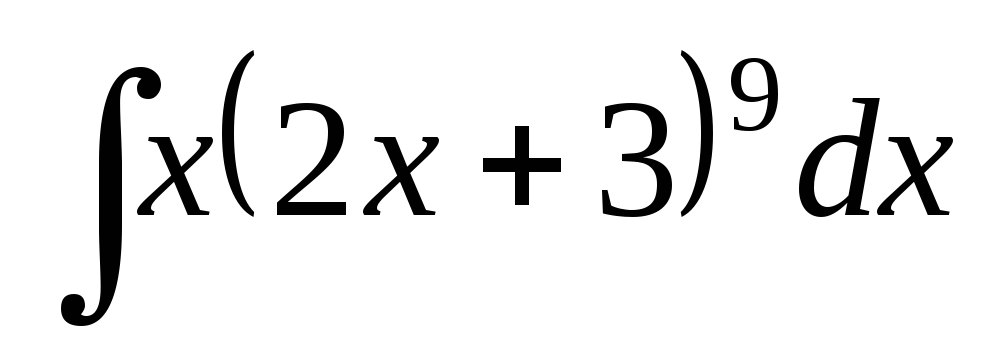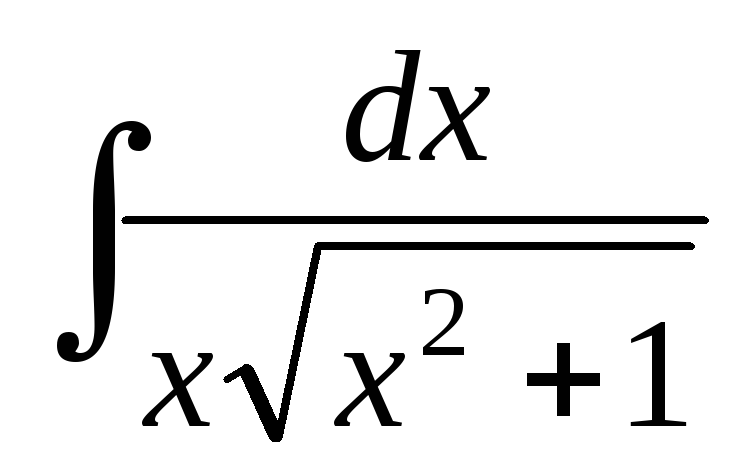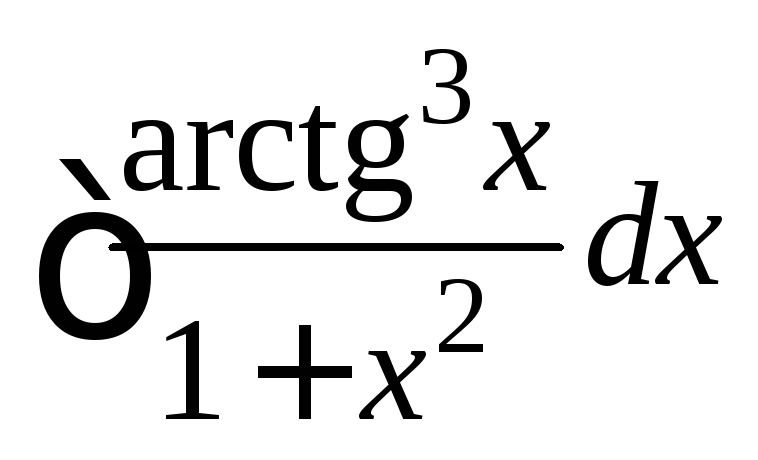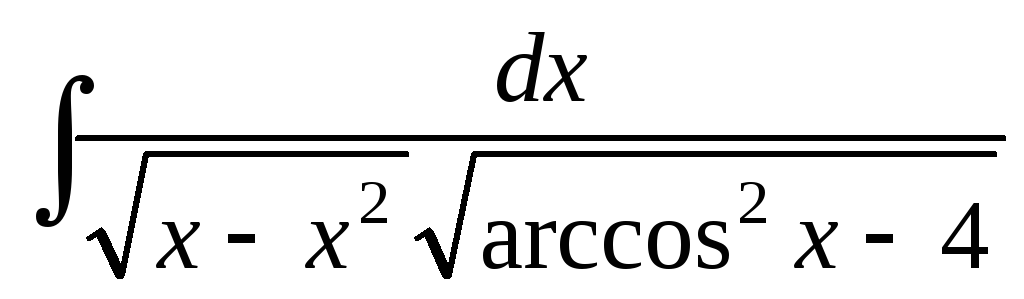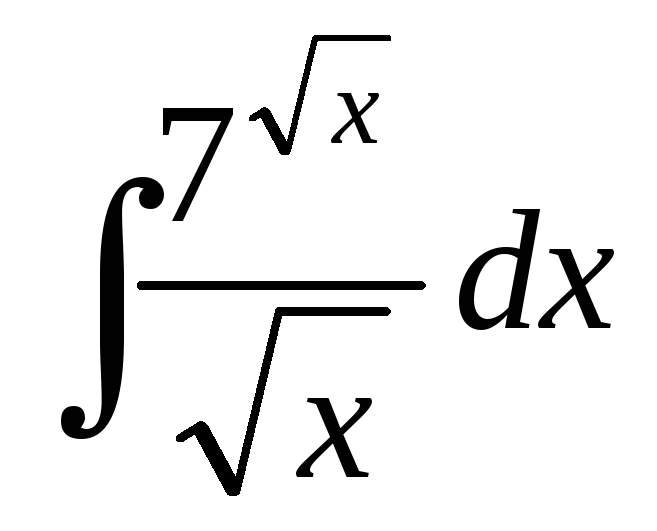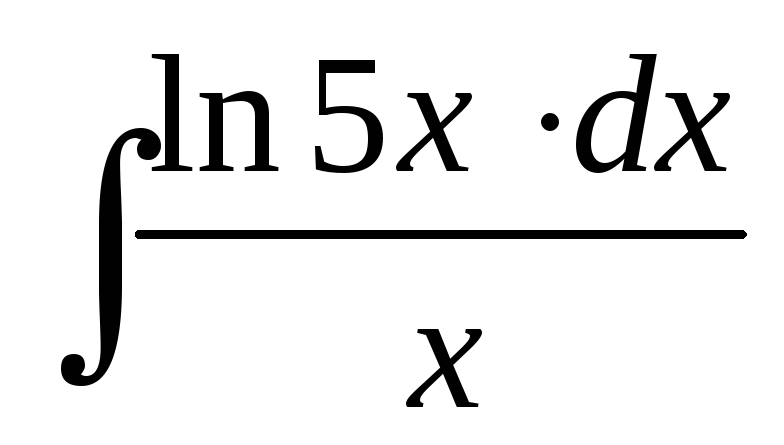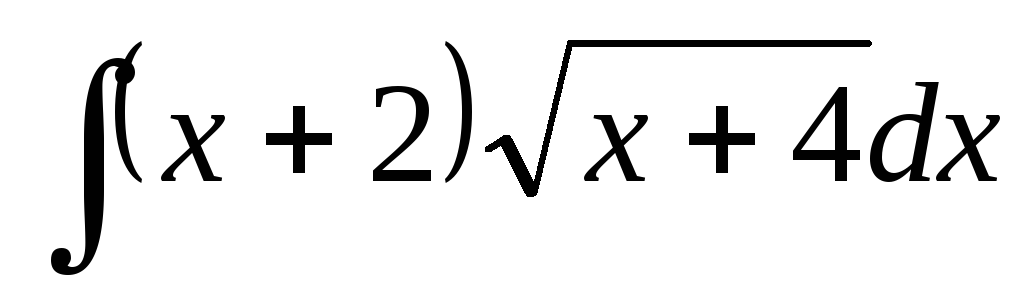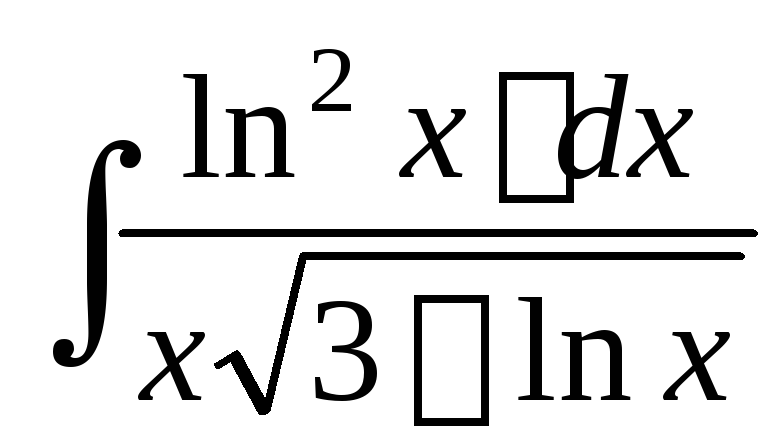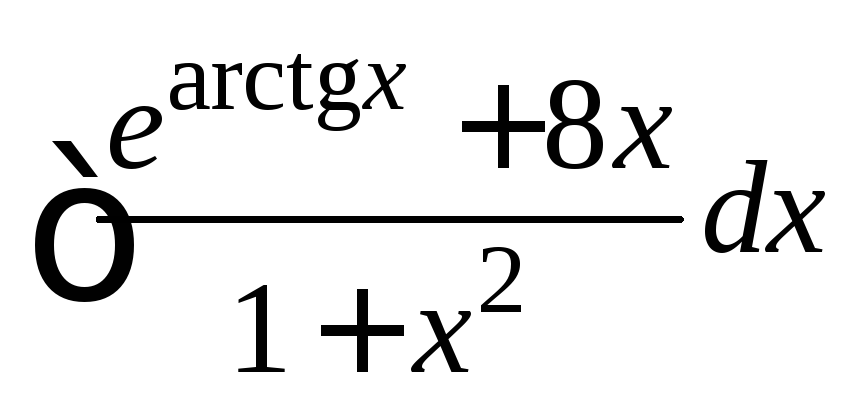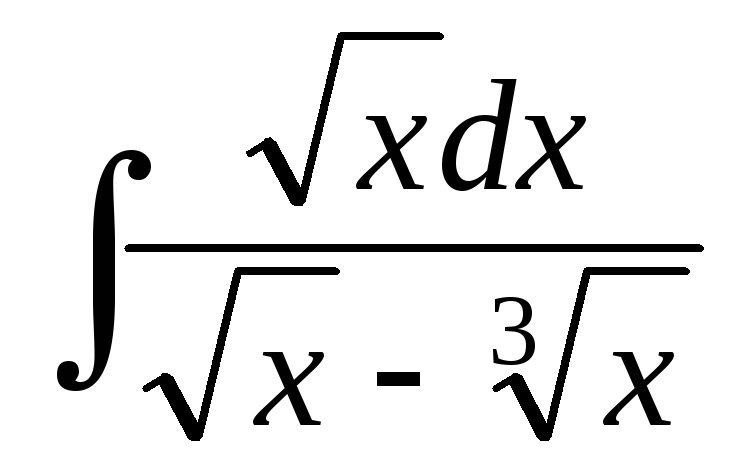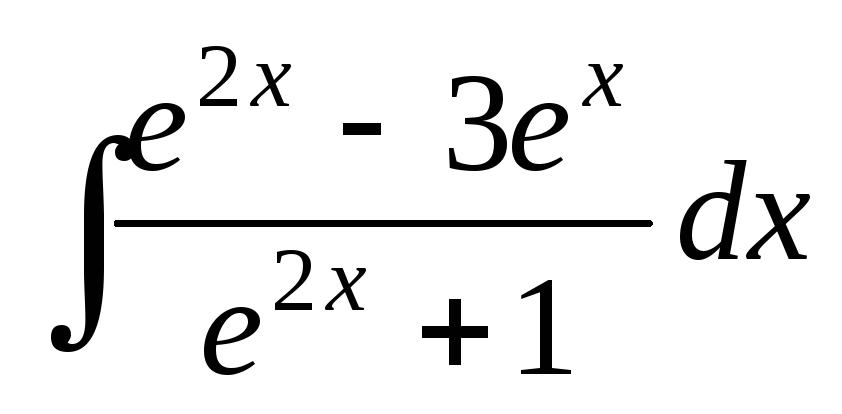6. Найти интегралы методом интегрирования по частям:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. .

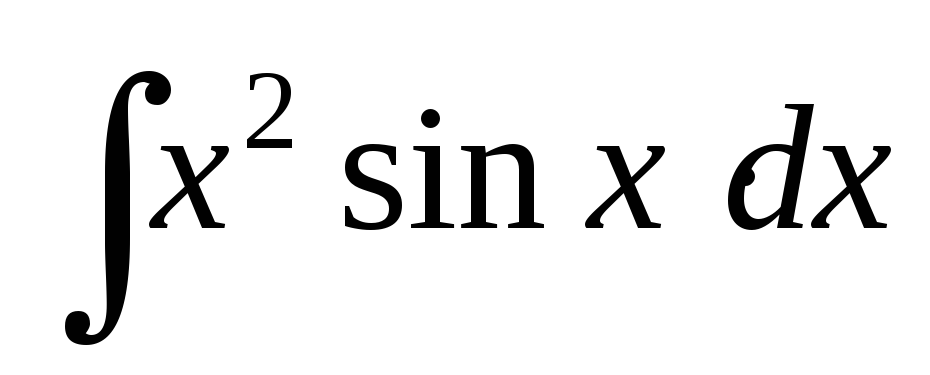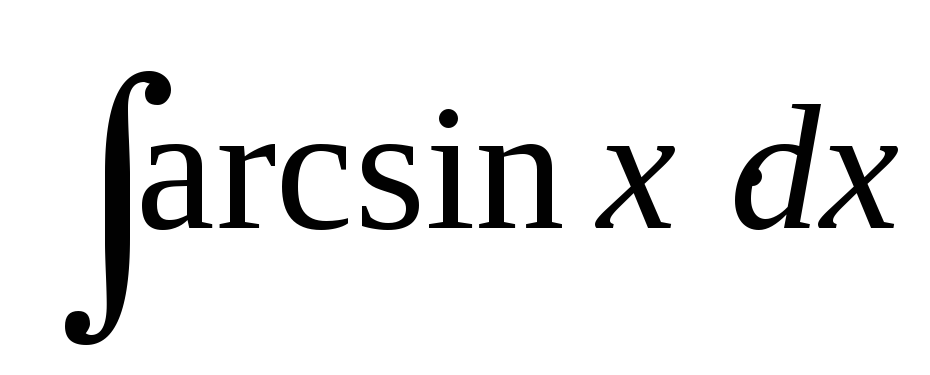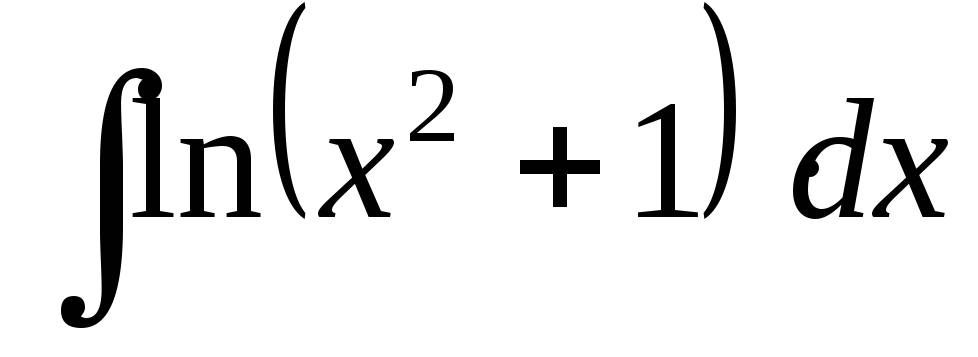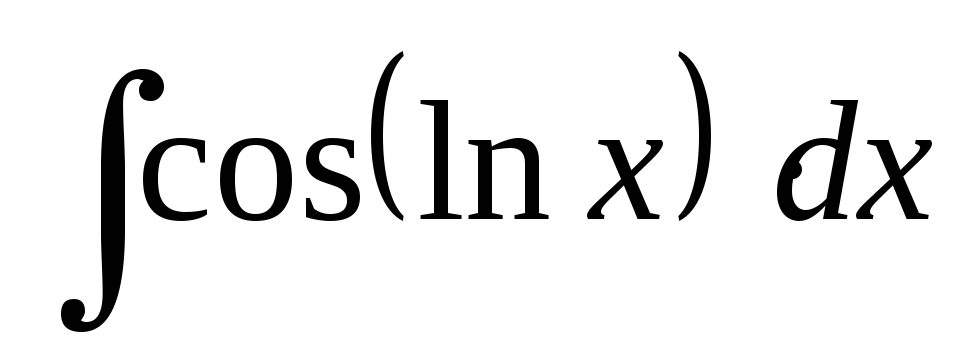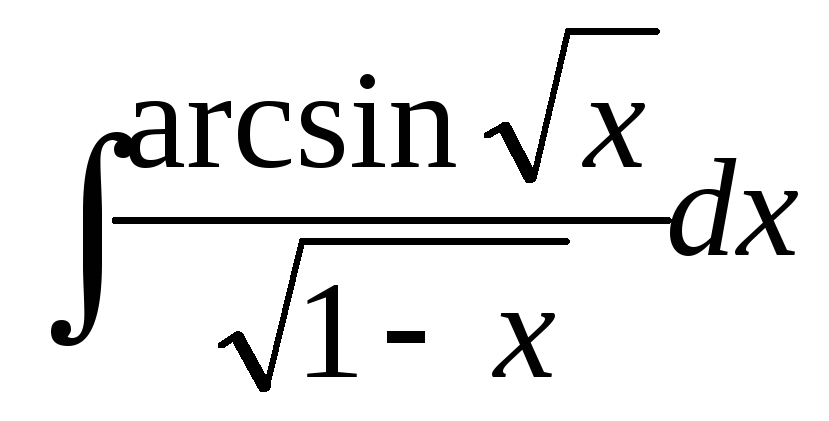Тема 2. Интегрирование рациональных функций

Вопросы для повторения:

1. Простейшие рациональные дроби и их интегрирование.

7. Теорема о разложении правильной рациональной дроби в сумму простейших дробей.

8. Способы нахождения неопределенных коэффициентов.

Пример 1. Разложить рациональную дробь в сумму простейших дробей. Используем метод неопределенных коэффициентов. Так как

.

Приводя к общему знаменателю и приравнивая числители получившихся дробей, приходим к равенству:

.

Два многочлена тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Приравнивая коэффициенты, получаем систему уравнений для определения А, В,CиD:

при х⁰: – А + В –D=O;

при х¹:2А + В –C + D=1;

при х²: – А + В+C + 2D=0;

при х³:2А + В –2C =0.

Решив эту систему, найдем А, В, C,D:

;;;.

Следовательно:

.

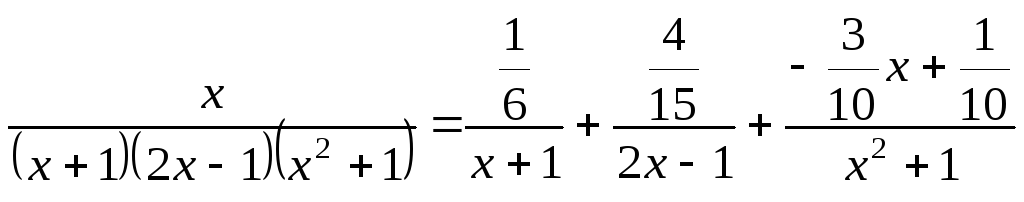Пример 2. Разложить рациональную дробь в сумму простейших дробей, используя метод частных значений. Так как

.

Приводя к общему знаменателю и приравнивая числители получившихся дробей, получим:

. (*)

Полагая в (*) х = 0, получаем 2 =А∙ (-1) ∙ 1 ∙ (-2), откудаА = 1;

полагая в (*) х = 1, получаем 3 =В∙ 1 ∙ 2 ∙ (-1), откуда;

полагая в (*) х = -1, получаем 1 =С∙ (-1) ∙ (-2) ∙ (-3), откуда;

полагая в (*) х = 2, получаем 4 =D∙ 2 ∙ 1 ∙ 3, откуда.

Следовательно:

.

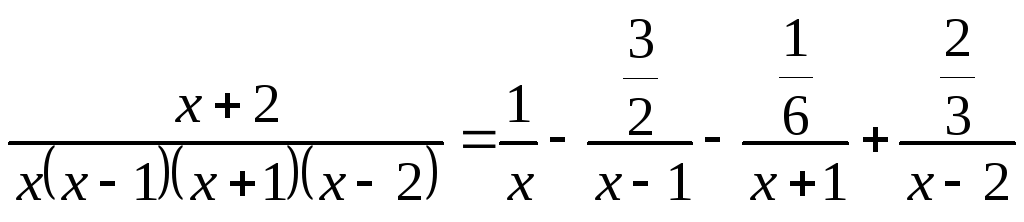Пример 3. Найти интегралы:

1)

Выделим в знаменателе подынтегрального выражения полный квадрат:

Получим:

2)

Выделим полный квадрат:

Получим:

3)

Выделим в знаменателе полный квадрат:

то

сделаем замену х– 3 =t,dx = dt,x = t+ 3, тогда получим

Пример 4. Найти интегралы от рациональных функций:

1)

Так как подынтегральная функция представляет неправильную рациональную дробь, то выделим целую часть:

тогда

.

2)

Представим подынтегральную функцию в виде суммы простейших дробей:

.

Приводя к общему знаменателю в правой части, приравниваем числители:

.

Сравнивая коэффициенты при одинаковых степенях х, получаем:

х²: 0 = А + В;

х: 1 = – 4А – 3В + С;

х⁰: 0 = 4А + 2В – С.

Из решения этой системы имеем: А = 1, В = -1, C= 2.

Таким образом,

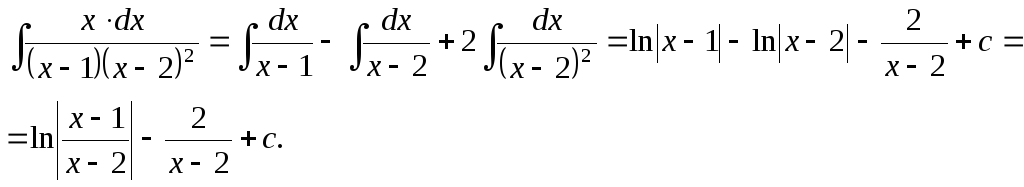
3)

Раскладываем знаменатель подынтегральной функции на множители, представим подынтегральную функцию в виде суммы простейших дробей:

.

Откуда

Составляем систему:

х³: 0 = А + С,

х²: 0 = В +D,

х: 0 = 4А,

х⁰: 1 = 4В.

Имеем: А = 0, ,C= 0,.

Таким образом,

4)

тогда пустьx+ 1 =t,dx=dt.

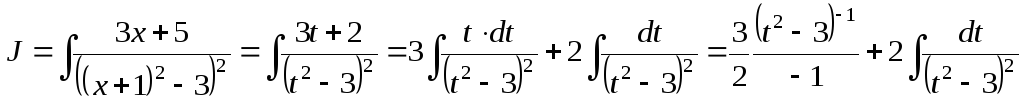
Применим к интегралу рекуррентную формулу

при n = 2, a² = 3, получим