Контрольная работа №2 по математике

для студентов 1 курса заочного отделения

факультета инновационных технологий в машиностроении специальностей:

1-370 106 техническая эксплуатация автомобилей;

1-360 104 оборудование и технологии высокоэффективных процессов обработки материалов;

(2-ой семестр)

Изучаемые разделы: Элементы высшей алгебры. Комплексные числа. Интегральное исчисление функций одной переменной. Дифференциальное исчисление функций многих переменных. Интегральное исчисление функций многих переменных. Векторный анализ и элементы теории поля.

1.Решение типового варианта.

Задача 1. Заданы два комплексных числа и . Вычислить+ , - , *, / . Найти модуль и аргумент комплексного числа и изобразить его на плоскости, записать число в тригонометрической и показательной форме, вычислить .

Решение.

По формулам суммы, разности и произведения комплексных чисел имеем

+ =

- =

* =

Для вычисления частного умножим числитель и знаменатель дроби на число сопряженное знаменателю и выполним преобразования

По формулам для определения модуля r и аргумента комплексного числа находим,

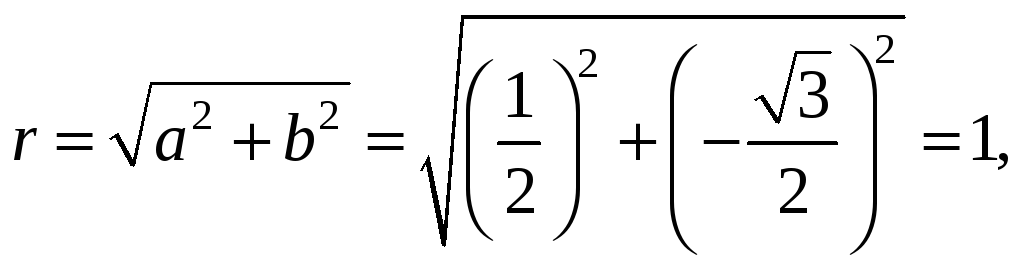
Тогда . Это означает, что

Показательная форма записи числа имеет вид

Изобразим на плоскости комплексное число

Для возведения комплексного числа в степень удобно воспользоваться формулой Муавра в тригонометрической или показательной форме.

Корень n-ой степени из комплексного числа z имеет n значений , k=0,1,…,n-1, которые находятся по формулам

- арифметический корень n-ой степени из r. Используя эти формулы, получаем

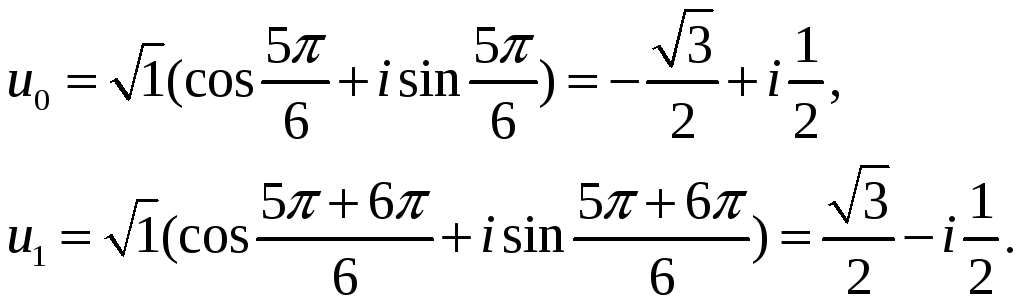
Задача 2. Используя ортогональное преобразование, привести к каноническому виду уравнение кривой и найти формулы преобразования координат.

Решение. Обозначим .

Матрица этой квадратичной формы имеет вид .

Составим характеристическое уравнение матрицы

.

Откуда .

Найдем собственные векторы. Для имеем систему уравнений

.

Тогда .

Нормируя полученные векторы, находим

.

Для получаем систему

.

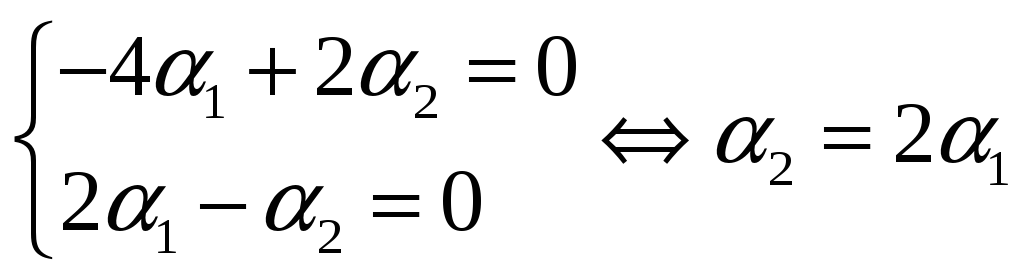Следовательно, .

Нормируя полученные векторы, имеем

.

Таким образом, матрица преобразования координат имеет вид

,

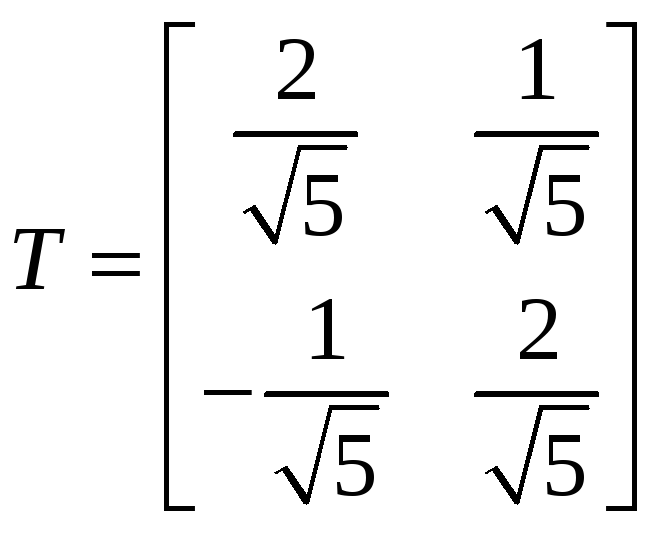формулы преобразования осей координат имеют вид

(1)

Подставив в уравнение данной кривой выражения для x и y из (1), имеем

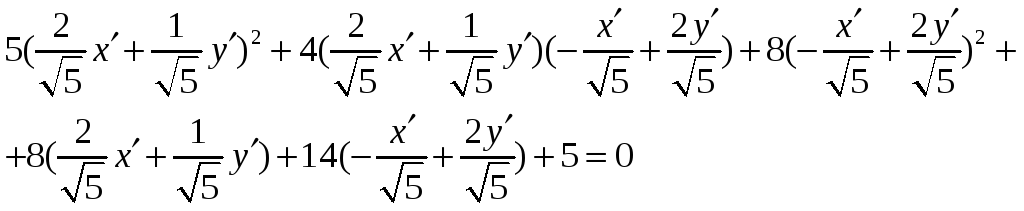
После несложных преобразований получим

.

Применив метод выделения полного квадрата, получим:

С помощью формул параллельного переноса системы координат

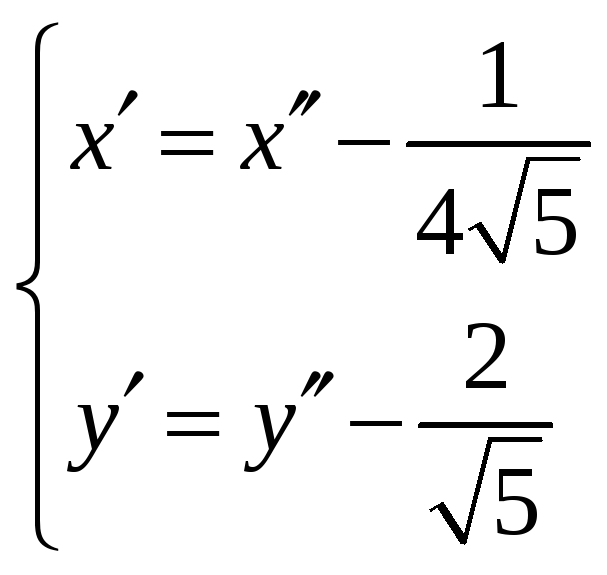
получаем

или .

Это уравнение эллипс с полуосями .

Задача 3. Найти неопределённые интегралы. В пунктах a и b результаты интегрирования проверить дифференцированием.

Решение.

3.a.

Преобразуем подынтегральную функцию таким образом, чтобы в числителе получилась производная знаменателя:

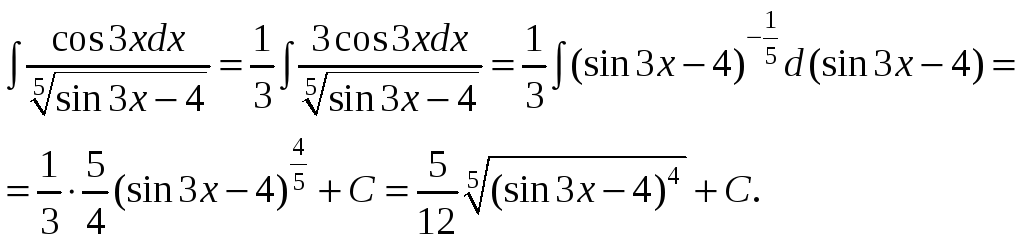
Проверим полученный результат:

3.b.

Воспользуемся методом интегрирования по частям, основанном на следующей формуле:

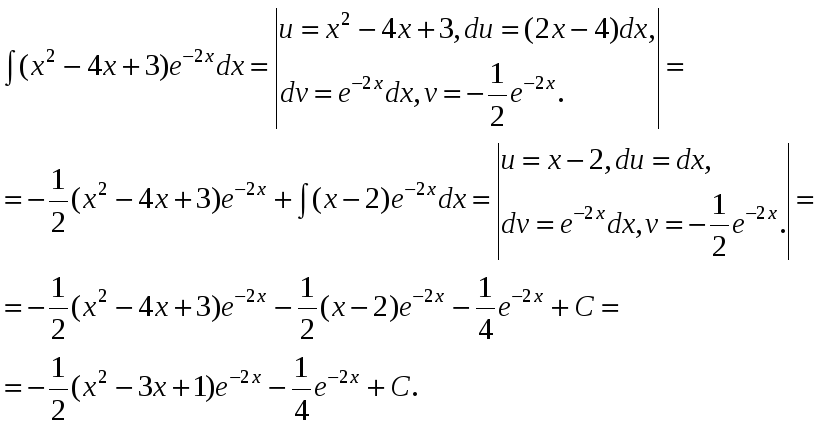
Выполним проверку результата:

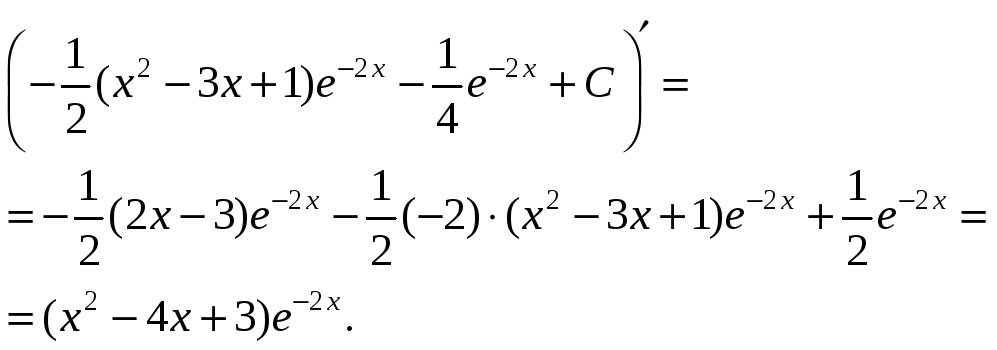
3.c.

Подынтегральная функция представляет собой рациональную дробь. Разложим её знаменатель на множители: тогда:

Приведя правую часть последнего равенства к общему знаменателю, и приравняв числители дробей, получим тождество:

Найдём искомые коэффициенты:

а) полагая , получаем , откуда ;

б) полагая , получаем , откуда ;

в) полагая , получаем , откуда ;

Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим:

3.d.

Подынтегральная функция представляет собой интеграл вида:

Где - рациональная функция; - целые положительные числа. С помощью подстановки (здесь - наименьшее общее кратное (НОК) знаменателей ) данный интеграл приводится к интегралу от рациональной функции.

Задача 4. Вычислить приближённое значение определённого интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления производить с округлением третьего десятичного знака.

Решение. Формула Симпсона или формула парабол имеет вид:

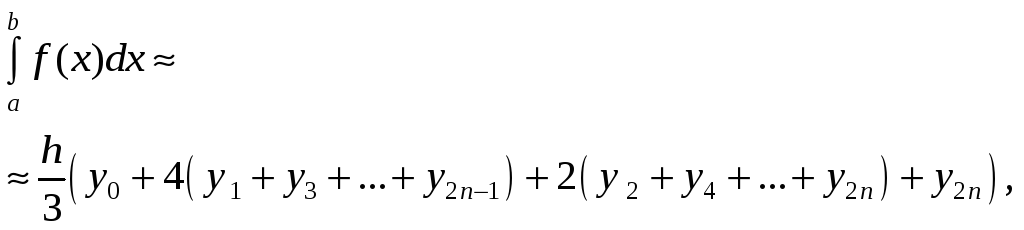(1)

где .

Рассмотрим при тогда .

Составим таблицу значений подынтегральной функции, необходимых для вычисления данного интеграла.

В последней строке таблицы находятся суммы чисел соответствующих столбцов.

Так как

по формуле (1) находим

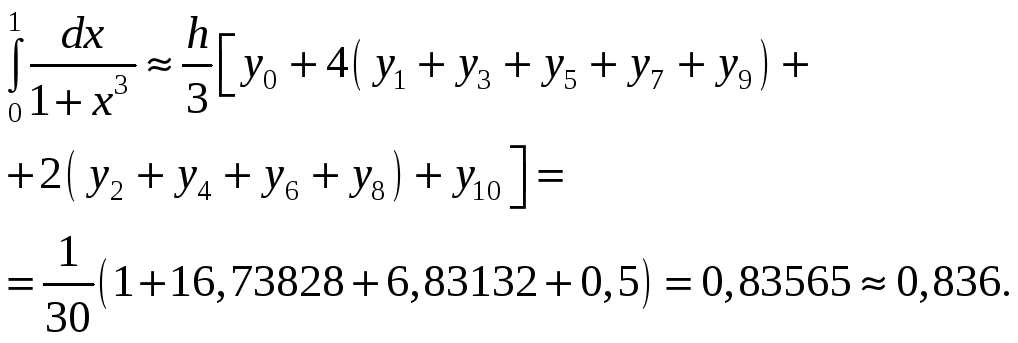
Задача 5. Вычислить несобственные интегралы или доказать их расходимость.

Решение. В соответствии определением несобственных интегралов имеем

5.a.

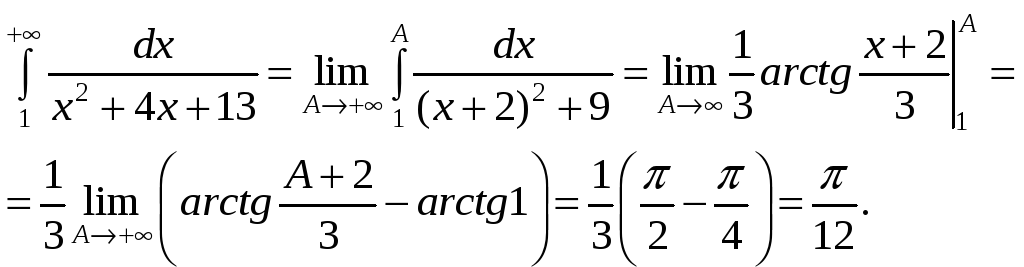
5.b.