Вариант 7

1. _{Дано действительное положительное число . Методом итераций решить систему линейных алгебраических уравнений с точностью . В данной задаче вычисление с точностью означает следующее. Вычисляется последо­вательность векторов приближенийx}^(m)_=(x1^(m)_,x2^(m)_,…,xn^(m)_{), где n—число неизвестных системы, m=0,1,2,... Если для некоторого k выполнено условие}

_{, i=1, 2, ..., n,}

_{x1=1.2-0.1x2-0.1x3 ,}

_{x2=1.3-0.2x1-0.1x3 ,}

_{x3=1.4-0.2x1-0.2x2}

2. _{Даны натуральные числа k, n, действительные числа a1,…,a k n. Получить последовательность mах(a1, ..., a k), max(a k+1, ...., a 2k), ..., max(a k(n-1)+1,…, a k n);}

3. _{Даны натуральное число n, целые числа a1, ... a25, b1,...bn. Среди a1, ..., a25 нет повторяющихся чисел, нет их и среди b1,..,bn. Построить пересечение последовательностей a1,…,a25 и b1,…,b n (т. e. получить в каком-нибудь порядке все числа, принадлежащие последовательности a1,…,a25 и последовательности b1,…,b n одновременно).}

4. _{Даны действительные числа х, у. Определить, принадлежит ли точка с координатами х, у заштрихованной части плоскости}

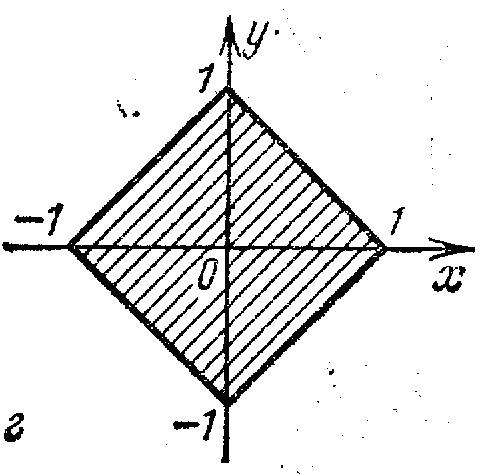
5. _{Дано натуральное число n. Выяснить, можно ли представить n! в виде произведения трех последовательных целых чисел.}

Вариант 8

1. _{Дано натуральное число п. Получить в порядке возрастания п первых натуральных чисел, которые не делятся ни на какие простые числа, кроме 2, 3 и 5}

2. _{Написать программу решения по методу Гаусса системы линейных уравнений}

_{10x1-x2+2x3-3x4=0,1}

_{x1-10x2-x3+2x4=0,}

_{2x1+3x2-20x3-x4=-10,}

_{3x1+2x2+x3+20x4=15;}

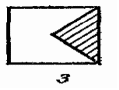3. _{Дана действительная квадратная матрица порядка п. Найти наибольшее из значений элементов, расположенных в заштрихованной части матрицы}

4. _{Даны целые числа а1,…,an (в этой последовательности могут быть повторяющиеся члены). Найти число различных членов последовательности.}

5. _{Дано действительное число e. Вычислить интегралс точностью e. В данной задаче вычисление с точностью e означает следующее. Отрезок интегрирования разбивается на ni равных частей и строится сумма Sn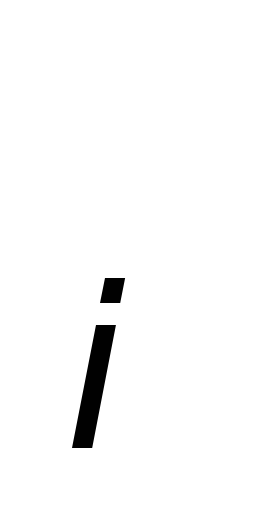,котораяявляется приближенным значением интеграла. Если выполняется условие 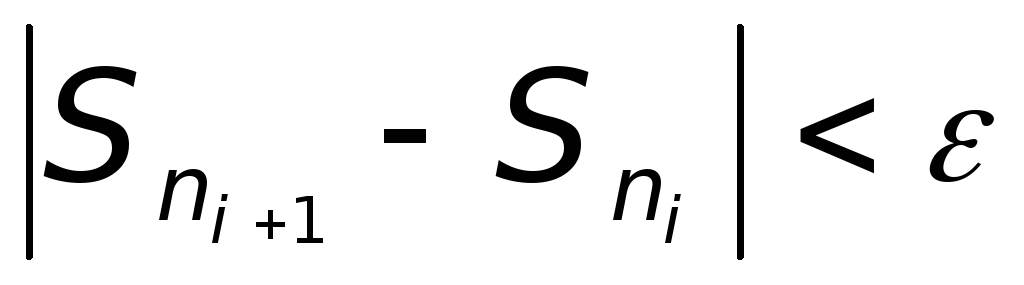, 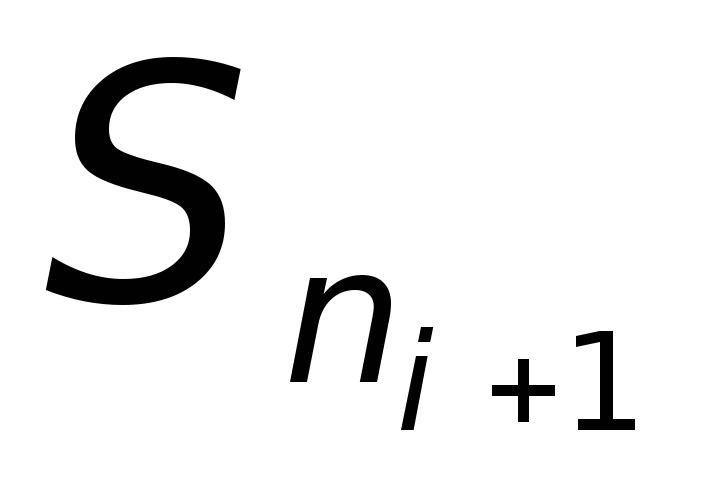считается значением интег­рала с точностью e. (Здесь ni < ni+1 (i=1, 2, ...).)}

Вариант 9

1. _{Даны натуральное число n, целые числа a1, ... a25, b1,...bn. Среди a1, ..., a25 нет повторяющихся чисел, нет их и среди b1,..,bn. Верно ли, что все члены последовательности b1,…,bn входят в последовательность a1,…,a25}

2. _{Дано действительное положительное число . Методом итераций решить систему линейных алгебраических уравнений с точностью . В данной задаче вычисление с точностью означает следующее. Вычисляется последо­вательность векторов приближенийx}^(m)_=(x1^(m)_,x2^(m)_,…,xn^(m)_{), где n—число неизвестных системы, m=0,1,2,... Если для некоторого k выполнено условие}

_{, i=1, 2, ..., n,}

_{5.92x1-1.24x2-1.84x3=2.44,}

_{2.72x1-9.71x2+2.43x3=2.4,}

_{1.76x1-3.12x2+9.38x3=1.93,}

3. _{Даны натуральные числа k, n, действительные числа a1,…,a k n. Получить: последовательность а1 + ... + a k, a k+1 + ... + а2k,..., a k (n-1)+1 + a k n ;}

4. _{Даны действительные числа х, у. Определить, при­надлежит ли точка с координатами х, у заштрихованной части плоскости}

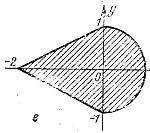
3. _{Дано натуральное число n. Среди чисел 1,2, ... ..., n найти все те, которые можно представить в виде суммы квадратов двух натуральных чисел.}