
Электричество и магнетизм
.pdf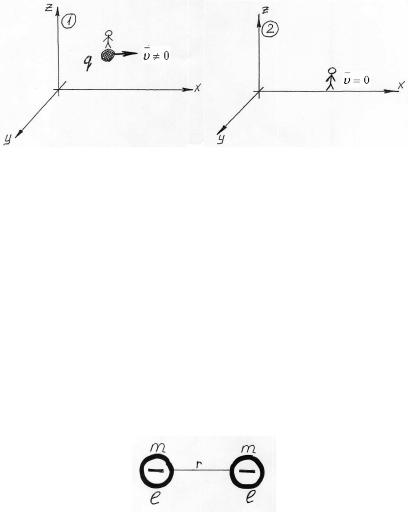
ЭЛЕКТРОМАГНЕТИЗМ
Лекция № 1
Электростатика.
Изучает взаимодействия неподвижных в данной системе отсчета зарядов. По современным представлениям, вокруг любого заряженного тела существует электромагнитное поле. Выделение электрической компоненты
этого поля – это вопрос выбора системы отсчета.
В обоих системах отсчета есть наблюдатели. В (1) находиться заряд q, неподвижный относительно этой системы и наблюдателя. Обоим наблюдателям задают один вопрос: «Какое поле существует вокруг заряда q?»
1наблюдатель: вокруг заряда существует электрическое (электростатическое) поле.
2наблюдатель: вокруг заряда существует электромагнитное поле.
Ответ второго наблюдателя объясняется тем, что заряд q двигается со скоростью относительно второго наблюдателя, то есть движение заряда представляет собой электрический ток.
Вокруг тока существует магнитное поле. Электрическое поле так же остается существующим вокруг этого заряда. И так, в самом общем случае, вокруг любого заряда всегда существует единое электромагнитное поле.
Взаимодействуют два электрона r 1м
m 10 30кг |
|
|
|
ВвакуумеF K |
q1q2 |
||
|
|
|
2 |
||||
e 1,6*10 19 Кл |
|
|
|
|
|||
|
|
|
|
|
|||
ВвеществеF K |
q1q2 |
|
|
|
|
|
|
r2 |
|
|
|
|
|
||
|
|
|
|
|
|
||
Гравитационное взаимодействие: F |
G |
m2 |
, |
|
|||
|
|
||||||
|
|
|
гр |
|
r2 |
|
|
|
|
|
1060 |
|
|
|
|
|
|
F 6,7*10 11 |
7*10 71. |
||||
|
|
|
|||||
|
|
гр |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Электромагнитное взаимодействие:
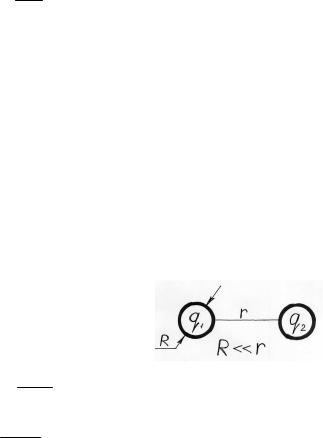
F k |
e2 |
|
103 *3*10 38 |
|
3*10 27 H , |
||||||
|
|
||||||||||
k |
|
r2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F |
3*10 27 |
|
44 |
|
43 |
|
|||||
эм |
|
|
|
|
|
0,5*10 |
|
|
5*10 |
|
раз. |
|
7*10 71 |
|
|
|
|||||||
F |
|
|
|
|
|
|
|||||
гр |
|
|
|
|
|
|
|
|
|
|
|
По современным представлениям, три элементарные частицы создают структуру всего мира (электрон, протон и нейтрон).
1.электрон – q = – е , me 9.1*10 31кг.
2.протон q = е , mp 1.7*10 27кг.
mp 1840 раз. me
3. нейтрон – заряда не имеет, нейтрален. mn mp .
Существует закон сохранения зарядов: в замкнутой системе отсчета полный заряд сохраняется. Величина заряда является абсолютной, т.е. не изменяется при переходе из одной системы отсчета к другой.Закон кратности заряда q N *e.
Закон Кулона.
Основным законом электростатики является закон Кулона, который объясняет взаимодействие точечных зарядов.
Точечным называют заряд размещенный на теле, размерами которого можно пренебречь.
F k q1q2 – закон Кулона 1796 год.
r2
k 1 – постоянная в законе Кулона.
4 0 k 9*109 .
0 8.85*10 12 Ф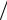 м – электрическая постоянная, физического смысла не имеет.
м – электрическая постоянная, физического смысла не имеет.
– диэлектрическая проницаемость среды.
1, |
вак 1, |
вода 81. |
Электростатическое поле.
Взаимодействие посредствам электрического поля происходит следующим образом: один из зарядов образует вокруг себя поле, каждая точка которого характеризуется напряженностью, являющейся векторной и силовой характеристикой поля. Если в эту точку поместить другой заряд, то на него со стороны поля первого заряда будет действовать сила:
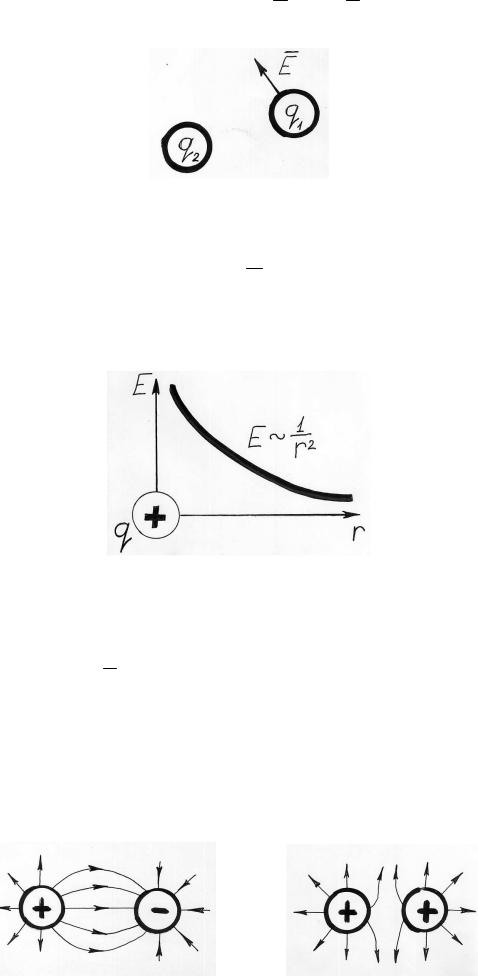
F q2 *E |
FE q*E. |
Таким образом, заряд является источником поля. Напряженность поля одиночного заряда определяется соотношением:
E F ,
|
|
q |
|
|
|
|
|
||||
|
q |
|
|
|
q |
* |
|
|
|
. |
|
E k* |
|
|
k* |
r |
|||||||
E |
|||||||||||
r2 |
r2 |
|
|
|
|||||||
|
|
|
|
|
r |
||||||
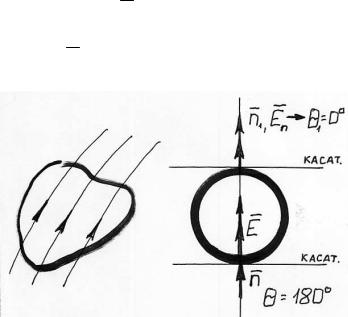
Силовые линии поля и их свойства.
Графически электростатическое поле изображается с помощью силовых
линий. Причем вектор E направлен по касательной к силовой линии. Силовая линия – это траектория движения свободного заряда в поле.
Свойства силовых линий:
1.Начинаются на положительных зарядах и заканчиваются на отрицательных зарядах (или в бесконечности). Как известно, разноименные заряды притягиваются, одноименные – отталкиваются.
2.Силовые линии не пересекаются (поскольку точка пересечения одновременно будет соответствовать двум значениям напряженности поля, что невозможно).
3. Густота силовых линий определяет величину напряженности поля.
Лекция № 2
Методы вычисления напряженности поля.
1. Одиночный заряд |
|
|
||
Для точечного заряда E k* |
q |
. Размер заряженного тела |
r. |
|
r2 |
||||
|
|
|
||
k 1 4 0
2. Принцип суперпозиции
Позволяет рассчитывать напряженность поля нескольких зарядов. Напряженность поля, создаваемого в некоторой точке пространства
произвольной системой зарядов, равна векторной сумме напряженностей создаваемых каждым из зарядов в отдельности:
EEi .
i– количество зарядов входящих в систему,
Ei – напряженность поля создаваемого каждым из зарядов системы, Е – результирующая напряженность поля всей системы зарядов, Из формулы следует что электростатические поля не взаимодействуют
друг с другом, а векторно складываются.
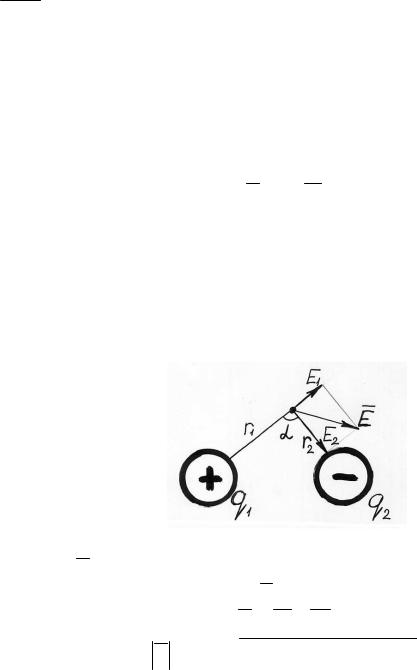
Напряженность поля двух точечных зарядов
Заданно: q1, q2, r1, r2, . Найти: E.
В начале найдем направление E. Из принципа суперпозиции і=2.
E E1 E2 ,
EE 
 E12 E22 2E1E2 cos .
E12 E22 2E1E2 cos .
Напряженность поля системы зарядов
Диполь – система из двух близко расположенных зарядов, имеющих
одинаковую величину и разные знаки.

Близкорасположенные – расстояние с которого наблюдается заряды много больше чем расстояние между ними (r l).
Каждый диполь обладает дипольным моментом, который равен произведению заряда на расстояние между зарядами. Причем дипольный момент это векторная величина, он направлен от отрицательного заряда к положительному.
|
|
|
|
|
|
|
|
p q*l, |
p q*l, |
l |
l |
||||
Рассмотрим 2 задачи для диполя.
1.Напряженность поля на прямой проходящей через середину оси диполя перпендикулярна к ней.
E E E ,
E E.
Величину напряженности поля диполя найдем из подобия треугольников.
E |
|
r |
2 |
|
l2 |
|
|
|
E |
*l |
|||||
|
|
|
|
|
|
||||||||||
|
|
|
4 |
|
E |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
||||
E |
|
|
l |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
r |
2 |
|
l2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
E k |
|
|
q |
|
|
, |
E k |
|
|
ql |
|
. |
|
r |
2 |
|
l2 |
|
(r |
2 |
|
l2 |
3 |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
) 2 |
|
||
|
4 |
|
|
|
|
4 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
2.Напряженность поля на оси диполя.
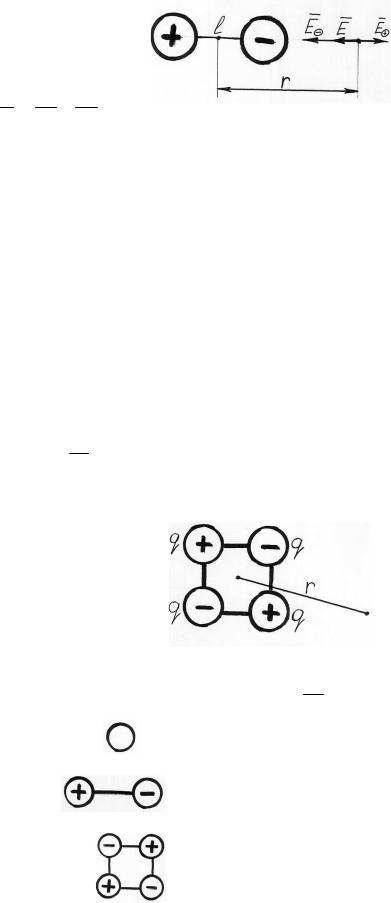
E E E ,
E E E ,
E |
k |
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(r |
|
|
|
l |
2 |
) |
2 |
, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E k |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(r |
|
|
l2 |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
2rl |
|
l |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
E kq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kq |
|
2kq |
|
, |
|||
|
|
|
|
|
l |
|
|
|
|
|
|
l |
|
r4 |
r3 |
|||||||||||
|
(r |
)2 |
|
|
(r |
)2 |
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p E 2k r3 .
Квадруполь
Дипольный момент квадруполя равен 0.
1
Напряженность поля квадруполя E ~ r4 ,
один заряд |
E ~ |
1 |
|
|
|
|||
r2 |
||||||||
|
|
|||||||
диполь |
E ~ |
1 |
|
|
||||
r3 |
||||||||
|
|
|
||||||
квадруполь |
E ~ |
1 |
. |
|||||
|
||||||||
|
|
|
|
r4 |
||||
С увеличением количества зарядов входящих в систему напряженность поля этой системы уменьшается.

3.Напряженность поля заряженных тел различной формы. Поток вектора напряженности. Теорема Остроградского-Гаусса.
Поток вектора напряженности через единичную, перпендикулярную силовым линиям вектора, площадку равен количеству силовых линий проходящих через эту площадку.
NE 2 NE E.
S 1 NE E*S – формула справедлива для однородного поля. Силовые линии однородного поля параллельны и эквидистактны.
Во всех точках однородного поля E имеет одинаковую величину и направление.
Для произвольно ориентированной площадки:
dS элемент. Бесконечно малая площадка.
(nE),
dS dS*cos , dNE EdS ,
dNE E*cos *dS,
En E*cos .
Получим dNE EndS .
В этом случае поток NE dNE EndS при неоднородном поле.
Поток через замкнутую поверхность.
NE  EndS
EndS
1.Рассмотрим поток вектора E в двух случаях.
а)Источник вектора E лежит вне замкнутой поверхности.
dNE 0,
dNE E*cos 1, где cos 1 1 dNE dNE
dNE 0,
dNE E*cos 2, где cos 2 1
Из этого следует, что полный поток через всю поверхность равен нулю. Если источники поля вне замкнутой поверхности, то потока через эту
поверхность они не создают.
б) Источники поля внутри замкнутой поверхности

Если заряд вокруг замкнутой поверхности, то возникает поток через эту поверхность.
На вопрос: «Чему равен поток?», отвечает теорема ОстроградскогоГаусса:
 Е dS 1 qi .
Е dS 1 qi .
S n 0
Поток через замкнутую поверхность окружающую произвольную систему зарядов равен алгебраической сумме зарядов, находящихся внутри этой системы.
Физический смысл теоремы Остроградского-Гаусса.
Электрическое поле имеет источники в виде электрических зарядов. Теорема Остроградского-Гаусса позволяет решать задачи о вычислении
напряженности поля заряженных тел различной формы.
Пример 1.
Напряженность поля заряженной сферы. Известны R, Q qi - общий заряд на ее поверхности.
Поле вне сферы r>R.

Окружим сферу воображаемой сферой радиусом r, и будем считать поток по теореме Остроградского-Гаусса поток через эту воображаемую сферу.
E En
SEdS |
1 |
Q S |
dS 4 r2 |
|
|||
|
0 |
|
|
Поскольку заряды неподвижны, напряженность поле const.
E4 r2 1 Q,
0
Q E 4 0r2 .
Поле внутри сферы. Поскольку внутри воображаемой поверхности заряды отсутствуют, поток через эту поверхность равен 0.
 S EndS 0,
S EndS 0,
dS 0,
En E 0,
E 0.
Внутри заряженной сферы электрическое поле отсутствует.
Представим графически полученные результаты.
