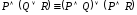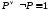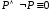Предикат ұғымы

Анықтама 1. x₁, x₂, …, x_n – пәндік айнымалылардың символдары болсын. Пәндік айнымалылардың (x₁, x₂, …, x_n) топтары пәндік аймақ деп аталатын  жиыныны тиісті болсын.  пәндік аймағында анықталған n-орынды предикат деп, -ның тұжырымдар жиынына бейнелеуін айтады.

Мысалдарды қарастырар алдын n-орынды предикаттарға квазианықтама берейік:

Анықтама. «n айнымалыға тәуелді және келесі қасиетке ие болған баяндамалы байланысты сөйлемі: айнымалылардың орнына анық мәндер қойылғанда ақиқат немесе жалған болсын».

Мысал 1. D(x₁, x₂) = «x₁ натурал саны x₂ натурал санына бөлінеді (қалдықсыз)» - NN жиынында анықталған екі орынды предикат. Түсінікті, D(4, 2)=1, D(3, 5)=0.

Мысал 2. Q(x) = «х₂<-1, xR» - R нақты сандар жиынында анықталған бір орынды предикат. Q(-1)=0, Q()=0. Q(x) – тепе-тең жалған екендігі түсінікті, яғни Q(x) 0.

Мысал 3. R(x, y, z)= «x²+ y²z; x, y, zR» - R³ жиынында анықталған үш орынды предикат. R(1, 1, -2)=0, R(1, 1, 2)=1.

Мысал 4. S(x, y) = «sin2ху>-3; x, yR» - екі орынды тепе-тең ақиқат предикат.

_Р(x1, x₂, …, x_n) -  аймағында анықталған n-орынды предикат болсын_{. Онымен келесі түрде анықталған екі жиынды байланыстырамыз:}

_IP={( x₁, x₂, …, x_n )  _{| Р(}x₁, x₂, …, x_{n)=1} – Р предикаттың ақиқаттық жиыны,}

_LP={( x₁, x₂, …, x_n)  _{| Р(}x₁, x₂, …, x_{n)=0} – Р предикаттың жалғандық жиыны.}

_{Анықтама 2. Р –} -да анықталған предикат болсын. Егер _IP= _{(LP=) болса, онда Р тепе-тең ақиқат, егер LP=} _{(IP=) болса, онда Р тепе-тең жалған предикат деп аталады.}

_{Егер IP }  _{және LP   болса, онда Р орындалатын предикат деп айтамыз.}

R³ кеңістікте 3 мысалдағы R(x, y, z) предикаттың _{IP және LP жиындарын көрсетейік}

Предикаттарға логикалық амалдарды қолдану

_{Анықтама} 3. _{Р –} -да анықталған предикат болсын. Р предикаттың терістеуі дегеніміз _{белгіленетін және} -да _{келесі түрде анықталған предикат:}

_P және Q – -да анықталған предикаттар болсын_.

_P және Q _{предикаттардың дизъюнкциясы (конъюнкциясы, импликациясы, эквиваленциясы) дегеніміз былай белгіленетін 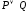, ( (,, PQ), , ) және -да келесі түрде анықталатын предикат:}

()

()

()

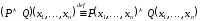Анықтама 4. Егер _{аймағына тиісті кез келген (} x₁, x₂, …, x_n ) пәндік айнымалылардың топтары үшін _Р( x₁, x₂, …, x_n ) _Q( x₁, x₂, …, x_n ) болса, онда P және Q предикаттар _{аймағында анықталған пара-пар предикаттар деп аталады (PQ).}

_{Теорема 1. аймағында анықталған} n – орынды предикаттардың жиыны предикаттардың бульдік алгебрасық құрайды, яғни олар үшін бульдік алгебраның келесі 19 негізгі тепе-теңдіктер орынды_:

0. 1. 2. 3. 4. 5. 6. 7. 8. 9.

10. 11. 12. 13. 14. 15. 16. 17. 18.

_{Мұнда 1 – -дағы тепе-тең ақиқат предикаттың, ал 0 – тепе-тең жалған предикаттың белгілері.}

Бұл теореманың дұрыстығы айқын. Өйткені предикаттарға қолданылатын амалдар тұжырымдарға қолданылатын амалдар көмегімен енгізілген, ал тұжырымдар бульдік алгебраны құрайды.