3.4.2 Точечные оценки параметров распределения

Т.к. X₁, X₂,…,X_n - независимые, одинаково распределенные случайные величины, то все они имеют один и тот же закон распределения вероятностей и одинаковые числовые характеристики.

Среднее выборочное удовлетворяет всем накладываемым к статистическим оценкам требованиям, т.е. дает несмещенную, эффективную и состоятельную оценку. Действительно:

. (3.7)

Это равенство следует из того, что все значения x_i распределены одинаково с математическим ожиданием . Поэтому является несмещенной оценкой .

В то же время эта оценка является состоятельной: согласно закону больших чисел, при увеличении n, величина сходится по вероятности к математическому ожиданию. Говорят, выборочное среднее обладает свойством статистической устойчивости.

Оценим по данным выборки неизвестную нам генеральную дисперсию D_Г. Поступим аналогично, т.е. в качестве оценки D_Г возьмем D_В. Можно доказать, что математическое ожидание D_В равно

.

Таким образом, D_В оказывается смещенной оценкой генеральной дисперсии, давая заниженное значение D_Г. Это значит, что при малых п, ее использование приведет к систематическим ошибкам. Для несмещенной оценки D_Г достаточно взять величину , которую называютисправленной дисперсией и обозначают s². Тогда

,

.

Т.о., математическое ожидание исправленной дисперсии действительно равно дисперсии генеральной совокупности и, значит, s² – состоятельная оценка генеральной дисперсии.

На практике для оценки генеральной дисперсии применяют исправленную дисперсию при . В остальных случаях, отклонениеD_В от D_Г малозаметно. Поэтому при больших значениях n ошибкой “смещения” 1/n можно пренебречь: т.к. при коэффициент, т.е.s² – состоятельная оценка.

Итак, несмещенная оценка для дисперсии имеет вид

(3.8)

для выборки, заданной последовательностью значений или таблицей относительных частот.

Пусть некоторая случайная величина X имеет математическое ожидание MX=m и дисперсию DX=. В ходе эксперимента получена случайная выборка из n независимых испытаний случайной величины X. Тогда справедливы следующие утверждения.

1) Среднее выборочное служит несмещенной и состоятельной оценкой математического ожиданияMX.

2) Если случайная величина X распределена по нормальному закону с параметрами N(m,), то среднее выборочное также распределено нормально и имеет минимальную дисперсию : т.е. . Поэтому среднее выборочное– эффективная и состоятельная оценка математического ожидания.

3) Выборочная дисперсия является смещенной оценкой генеральной дисперсии. Несмещенной оценкой генеральной дисперсииявляется «исправленная» дисперсия, для получения которой необходимо умножитьна так называемуюпоправку Бесселя . Тогда

.

«Исправленная» выборочная дисперсия является состоятельной оценкой генеральной дисперсии.

4. Если известно m – математическое ожидание случайной величины X, то выборочная дисперсия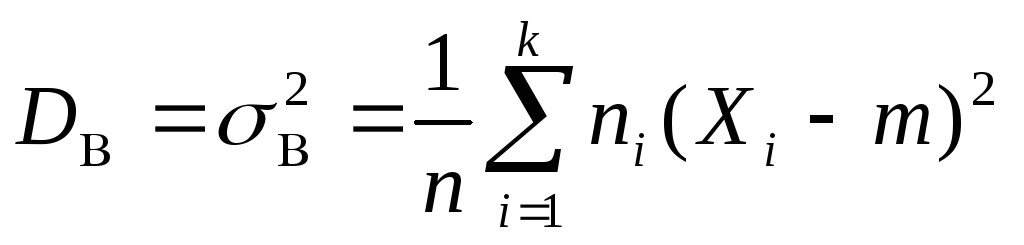является несмещенной, состоятельной и эффективной оценкой генеральной дисперсии.

5. Относительная частота является несмещенной и состоятельной оценкой вероятностиP(X=x_i). Эмпирическая функция распределения – накопленная относительная частота – является несмещенной и состоятельной оценкой теоретической функции распределенияF(x)=P(X<x).

Задача 5. Найти несмещенные оценки математического ожидания и дисперсии по таблице выборки:

xi	2	6	12
ni	3	10	7

Решение:

Из таблицы имеем объем выборки n = 20. Несмещенная оценка математического ожидания есть среднее выборочное :

Для вычисления несмещенной оценки дисперсии сначала найдем выборочную дисперсию, а затем несмещенную оценку – s²_:

, .

хi	2	6	12
	0.15	0.5	0.35

Задача 6. Найти несмещенные числовые характеристики выборки, заданной таблицей:

Решение:

Среднее выборочное является несмещенной оценкой генерального среднего, а для вычисления несмещенной дисперсиипредварительно вычислим смещенную дисперсию

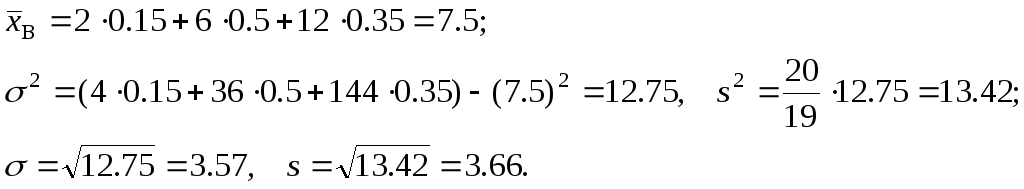
Легко видеть, что задачи 5 и 6 задают одну и ту же выборку, но в задаче 5 она задается таблицей абсолютных частот, а в задаче 6 – таблицей относительных частот:

=.

На практике если значение вариант x_i – большие числа, то для облегчения расчетов их представляют в виде суммы некоторого постоянного числа с и условной варианты u_i, как дополнения до , т.е.. Это значит, что задан некий новый вариационный ряд для величиныU, определенный по выборочным данным u_i. Поскольку выбор с произволен, то лучше взять за с значение, близкое к . Тогда,, а дисперсия не изменится, т.е., так как по свойствам дисперсии

, где C – const. Тогда

. Аналогично вычисляется несмещенная оценка дисперсии:

. (3.9.)

Если первоначальные варианты представлены десятичными дробями, то их умножают на постоянное число с=10^k, где k – количество десятичных знаков. Тогда условные варианты имеют вид , то есть дисперсия увеличилась в раз, согласно свойству дисперсии. Поэтому, а.

Аналогично, . (3.10)

Задача 7. Из генеральной совокупности извлечена выборка. Найти несмещенную оценку генеральной средней и генеральной дисперсии.

xi	3250	3270	3280
ni	2	5	3

Решение: 1. Найдем условную варианту и составим для нее ряд распределений:

Пусть с=3270, тогда ,

ui	-20	0	10
ni	2	5	3

2. Т.к. объем выборки n=10, то ;.

3. Найдем выборочную дисперсию для первоначальной варианты с помощью условной варианты: .

4. Найдем «несмещенную выборочную дисперсию» – несмещенную оценку генеральной дисперсии: .

То, что выбор постоянной с не влияет на значение дисперсии, следует из соответствующего свойства, известного теории вероятностей. Поэтому выбор постоянной с весьма условен и определяется удобством расчета. Особенно это очевидно при очень малых значениях V: например, если среднеквадратичное отклонение порядка 10^-7, а выборочное среднее порядка 10⁷, то затруднительно непосредственно вычислить дисперсию, т.к. незначительная разница будет меньше погрешности округления на микрокалькуляторе. Т.о., на практике исходят из критерия удобства дальнейших расчетов.