3.5.2 Доверительный интервал для оценки математического ожидания нормального распределения при известном среднем квадратическом отклонении 

Пусть произведена выборка из генеральной совокупности, подчиненной закону нормального распределения XN(m;). Это основное предположение математической статистики основано на центральной предельной теореме. Пусть известно генеральное среднее квадратическое отклонение , но неизвестно математическое ожидание теоретического распределения m (среднее значение ).

В таком случае среднее выборочное , полученное в ходе эксперимента (п.3.4.2), также будет являться случайной величинойm;). Тогда «нормализованное» отклонениеN(0;1) – является стандартной нормальной случайной величиной.

Задача состоит в поиске интервальной оценки для m. Построим двусторонний доверительный интервал для m так, чтобы истинное математическое ожидание принадлежало ему с заданной вероятностью (надежностью) .

Установить такой интервал для величины – это значит найти максимальное значение этой величиныи минимальное, которые являются границам критической области:.

Т.к. такая вероятность равна , то корень этого уравненияможно найти с помощью таблиц функции Лапласа (Таблица 3, приложение 1).

Тогда с вероятностью  можно утверждать, что случайная величина , то есть искомое генеральное среднее принадлежит интервалу . (3.13)

Величину(3.14)

называют точностью оценки.

Число – квантиль нормального распределения – можно найти как аргумент функции Лапласа (Таблица 3, приложение 1), учитывая соотношение 2Ф(u)= , т.е. Ф(u)= .

Обратно, по заданному значению отклонения  можно найти, с какой вероятностью, неизвестное генеральное среднее принадлежит интервалу . Для этого нужно вычислить

. (3.15)

Пусть из генеральной совокупности извлечена случайная выборка методом повторного отбора. Из уравнения можно найти минимальный объем повторной выборки n, необходимый для того, чтобы доверительный интервал с заданной надежностью не превышал наперед заданного значения. Оценку требуемого объема выборки производят по формуле:

. (3.16)

Исследуем точность оценки :

1) При возрастании объема выборки n величина  уменьшается, и значит, точность оценки увеличивается.

2) С увеличением надежности оценки увеличивается значение аргументаu (т.к. Ф(u) монотонно возрастает) и значит увеличивается . В таком случае увеличение надежности уменьшает точность ее оценки .

Далее символ всюду будет обозначать выборочное среднее.

Оценку (3.17)

называют классической (где t — некий параметр, зависящий от и n), т.к. она характеризует наиболее часто встречающиеся законы распределения.

3.5.3 Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном среднем квадратическом отклонении 

Пусть известно, что генеральная совокупность подчинена закону нормального распределения XN(m;), где величина среднего квадратического отклонения неизвестна.

Для построения доверительного интервала оценки генерального среднего в этом случае используется статистика , имеющая распределение Стъюдента с k=n–1 степенями свободы. Это следует из того, что 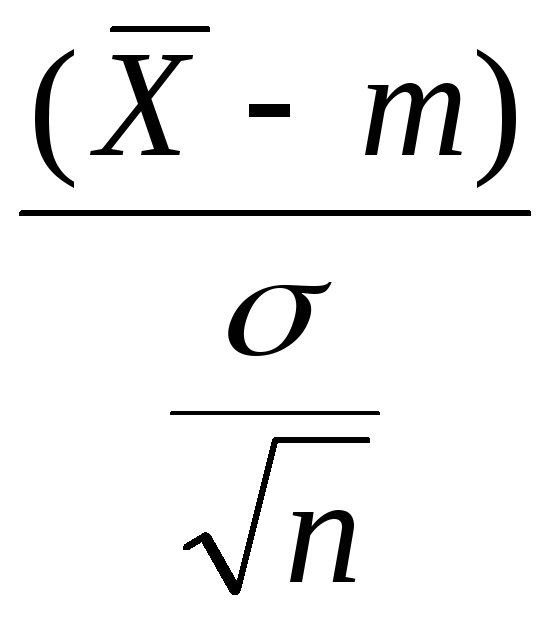N(0;1) (см. п.3.5.2), а (см. п.3.5.3) и из определения распределения Стъюдента (ч.1.п.2.11.2).

Найдем точность классической оценки распределения Стъюдента: т.е. найдем t из формулы (3.17). Пусть вероятность выполнения неравенства задана надежностью  :

. (3.18)

Поскольку TSt(n-1), очевидно, что t зависит от  и n, поэтому обычно пишут .

Тогда

(3.19)

где – функция распределения Стъюдента сn-1 степенями свободы.

Решая это уравнение относительно m, получим интервал который с надежностью  покрывает неизвестный параметр m.

Величина t_,n-1, служащая для определения доверительного интервала случайной величины T(n-1), распределенной по Стъюденту с n-1 степенями свободы, называется коэффициентом Стъюдента. Его следует находить по заданным значениям n и  из таблиц «Критические точки распределения Стьюдента». (Таблица 6, приложение 1), которые и представляют собой решения уравнения (3.19).

В итоге получаем следующее выражение точности  доверительного интервала для оценки математического ожидания (генерального среднего), если неизвестна дисперсия:

(3.20)

Т.о., существует общая формула построения доверительных интервалов для математического ожидания генеральной совокупности:

, (3.21)

где точность доверительного интервала  в зависимости от известной или неизвестной дисперсии находится по формулам соответственно 3.16. и 3.20.

Задача 10. Проведены некоторые испытания, результаты которых занесены в таблицу:

i	1	2	3	4	5
xi	-25	34	-20	10	21

Известно, что они подчиняются закону нормального распределения с . Найти оценкуm* для математического ожидания m, построить для него 90% доверительный интервал.

Решение:

1. Найдем m* =(-25+34-20+10+21)/5= 4 как среднее значений варианты x.

2. По доверительной вероятности найдем аргумент функции Лапласа (Таблица 3, приложение 1): .

3. Тогда точность оценки равна .

4. Доверительный интервал для m имеет вид 4-1.47<m<4+1.47, или 2.53<m<5.47.

Итак, m(2.53;5.47).

Задача 11. Глубина моря измеряется прибором, систематическая ошибка которого равна 0, а случайные ошибки распределяются по нормальному закону, со средним квадратическим отклонением =15м. Сколько надо сделать независимых измерений, чтобы определить глубину с ошибками не более 5м при доверительной вероятности 90%?

Решение:

По условию задачи имеем XN(m;), где =15м, =5м, =0.9. Найдем объем n.

1) С заданной надежностью = 0.9 найдем по таблицам 3 (Приложение 1) аргумент функции Лапласа u_=1.65.

2) Зная заданную точность оценки =u_=5, найдем. Имеем

. Поэтому число испытаний n25.

Задача 12. Выборка температуры t за первые 6 дней января представлена в таблице:

№	1	2	3	4	5	6
t1	-35	-32	-26	-35	-30	-17
t2	-31	-27	-28	-35	-40	-31

Найти доверительный интервал для математического ожидания m генеральной совокупности с доверительной вероятностью и оценить генеральное стандартное отклонение s.

Решение:

1. Несмещенную оценку найдем по формуле:

и .

2) Несмещённую оценку найдем по формуле:

	-35	-32	-26	-35	-30	-17	=-175
	- 5.8	-2.8	32	-5.8	-0.8	12.2
	33.64	7.84	10.24	33.64	0.64	148.84	=234.84

; ;

	-31	-27	-28	-35	-40	-31	=-192
	1	5	4	-3	-8	1
	1	25	16	9	64	1	=116

.

3) Поскольку генеральная дисперсия неизвестна, но известна ее оценка, то для оценки математического ожидания m используем распределение Стъюдента (Таблица 6, приложение 1) и формулу (3.20).

Т.к. n₁=n₂=6, то , , s₁=6.85 имеем: , отсюда -29.2-4.1<m₁< -29.2+4.1.

Поэтому -33.3<m₁<-25.1.

Аналогично имеем, , s₂= 4.8, , поэтому

–34.9< m₂< -29.1. Тогда доверительные интервалы примут вид: m₁(-33.3;-25.1) и m₂(-34.9;-29.1).

В прикладных науках, например, в строительных дисциплинах, для оценки точности объектов используются таблицы доверительных интервалов, которые приведены в соответствующей справочной литературе.