3.6.4 Гипотезы о числовом значении дисперсии

При проверке гипотезы о числовом значении дисперсии принеизвестном среднем m используют статистику

или , (3.42)

имеющую распределение сn-1 степенями свободы.

1. Границы критической области в этом случае ищут по таблицам распределения Пирсона ().

Критерии проверки гипотезы с помощью статистикипри уровне значимостипредставлены в таблице 9:

Таблица 8

№ п/п	Виды альтернативных гипотез H1	Критерий отклонения H0 по статистике	Графическая иллюстрация для x2
1		правосторонний критерий
2		левосторонний критерий
3		,двусторонний критерий

Наблюдаемые значения статистики вычисляются по соответствующим формулам и сравниваются с числовым значением критерия.

2. Сравнение дисперсий двух генеральных совокупностей – часто встречающаяся практическая задача. Основная гипотеза заключается в равенстве этих дисперсий, т.е.H₀:, тогда альтернативная гипотеза может быть двух видов: либо , либо. Оценку дисперсиипроизводят по исправленным выборочным дисперсиям, с учетом, что,пользуясь F-распределениями Фишера-Снедекора

(3.43)

с истепенями свободы. Критерии проверки гипотезыH₀: по статистике F для уровня значимости представлены в виде таблицы, причем границы критической областиберутся из затабулированных значений критических точек распределения Фишера (Таблица 7, приложение 1):

Виды альтернативных гипотез H1	Критерий отклонения гипотезы H0 по статистике

Задача 17 (Свиридова Т.В., 2004г.) Две программы обрабатывают сигналы от драйверов. Первая программа обработала 10сигналов, вторая – 12 сигналов. По данным выборки рассчитаны выборочные дисперсииD₁X=7.3, D₂X=6.2. На уровне значимости α=0.05 выяснить, можно ли утверждать, что программы работают с одинаковой точностью?

Решение: Имеем n₁=10, n₂=12, D₁X=7.3, D₂X=6.2, α=0.05.

1) Проверим гипотезу о сравнении двух дисперсий нормальных генеральных совокупностей. Тогда основная гипотеза о том, что программы работают с одинаковой точностью H₀: _, альтернативная гипотеза о том, что программы работают с разной точностью Н₁: .

2) Найдем исправленные дисперсии:

,

.

3) Воспользуемся распределением Фишера-Снедекора.

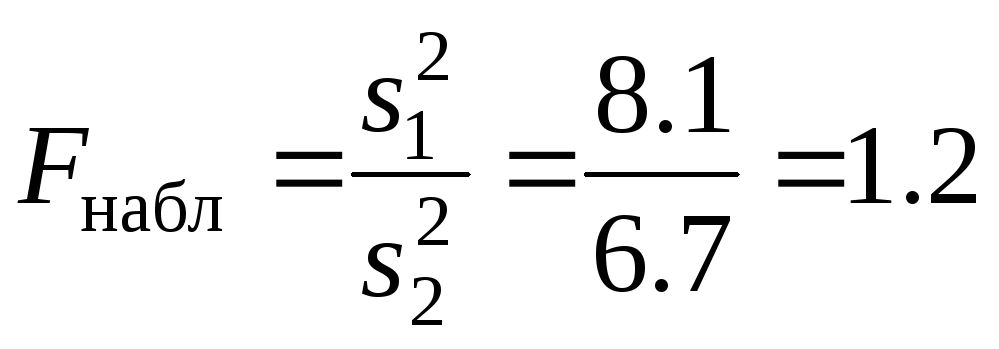
4) Ищем границу критерия: .

Т.к. 1.2<2.9, то , т.е. нет оснований отвергать Н₀. Значит_, программы работают с одинаковой точностью.

Задача 18 (Свиридова Т.В., 2004г.). Точность работы программы проверяют по дисперсии контролируемого количества символов в коде, которая не должна превышать 0.1. По выборке из 15 сообщений вычислена исправленная оценка дисперсии 0.22. При уровне значимости 0.05 проверить, обеспечивает ли программа необходимую точность?

Решение:

Имеем: n=15, s²=0.22, α=0.05, σ²<0.1.

1) Формулируем гипотезу о числовом значении дисперсии:

Н₀: программа обеспечивает необходимую точность σ²=0.1.

Н₁: программа не обеспечивает необходимую точность σ²>0.1

2) Найдем статистику χ²: .

3) Ищем границы критерия: χ²_0.05;14=23.7

4) Т.к. 30.8>23.7, то χ²> χ²_0.05;14.

Следовательно, принимаем гипотезу Н₁.

Вывод: программа не обеспечивает необходимую точность.