3.6.3 Сравнение генеральных средних двух нормально распределенных совокупностей

1) Пусть имеются две большие независимые выборки x₁, x₂,…, x_n и y₁, y₂,…,y_m (n>30, m>30), извлеченные из генеральных совокупностей X и Y, имеющие объемы соответственно n и m, причем известны их средние выборочные ии дисперсиии, но неизвестны генеральные средние (математические ожидания)_x и _y.

Проверим гипотезу H₀ о том, что _x=_y на уровне значимости .

По выборке необходимо вычислить наблюдаемое значение статистики Z:

, (3.39)

которая при выполнении гипотезы H₀ имеет нормированное нормальное распределение N(0,1).

Значение статистики Z сравнивают со значением соответствующего критерия, который находят по таблице критических точек функции Лапласа по заданному уровню значимости  из уравнения:

Ф(z_кр.)=для двусторонней критической области, еслиH₁: _x_y;

Ф(z_кр.)=для правосторонней критической области, еслиH₁:_x>_y.

2) Пусть имеются две малые независимые выборки x₁, x₂,…, x_n и y₁, y₂,…,y_m (n<30, m<30), извлеченные из генеральных совокупностей X и Y, имеющие объемы соответственно n и m, причем известны их средние выборочные , но неизвестны генеральные средние (математические ожидания)_x и _y. Пусть их неизвестные дисперсии предположительно равны между собой: .

Проверим гипотезу H₀ о том, что _x=_y на уровне значимости .

По выборке необходимо вычислить наблюдаемое значение статистики Т:

, (3.40)

где и– исправленные дисперсии соответственно первой и второй выборки,и– смещенные дисперсии соответственно первой и второй выборки.

Значение статистики Т сравнивают со значением соответствующего критерия, который находят по таблице критических точек распределения Стьюдента, по заданному уровню значимости  и числу степеней свободы k=n+m-2:

(3.41)

где .

а) Пусть основная гипотеза H₀: _x_y, альтернативная – H₁: _x_y. Двусторонняя критическая область для проверки гипотезы: , гдеt_{n+m-2; } находят по таблице 6 критических значений распределения Стьюдента, причем  в верхней строчке.

б) Пусть основная гипотеза H₀: _x_y, а альтернативная гипотеза H₁: _x_y. Правосторонняя критическая область для проверки гипотезы: , гдеt_n+m-2; находят по таблице 6 критических значений распределения Стьюдента, причем  в нижней строчке.

в) Пусть основная гипотеза H₀: _x_y,а альтернативная гипотеза H₁: _x_y. Левосторонняя критическая область для проверки гипотезы: , гдеt_n+m-2; находят по таблице 6 критических значений распределения Стьюдента, причем  в нижней строчке .

Если вычисления значения статистики Т попадает в критическую область, то основная гипотеза H₀ отвергается, и принимается альтернативная гипотеза H₁. Вероятность попадания в эту область равна уровню значимости .

Задача 16. Анализ ежедневного объема продаж за I квартал текущего года показал, что для 42 торговых точек Автозаводского района средний ежедневный объем продаж составляет 64 тыс. рублей, а для 20 торговых точек Центрального района – 62 тыс. рублей, при среднеквадратических отклонениях, соответственно, равных 4 и 5 тыс. рублей. Существует ли различие между ежедневным объемом продаж в Автозаводском и Центральном районах на 5% уровне значимости?

Решение. Имеем: .

Предположим, ежедневный объем продаж подчинен нормальному закону распределения, для которого неизвестны математическое ожидание и среднее квадратическое отклонение.

Проверяется гипотеза , при альтернативной гипотезе .

Вычисляем наблюдаемое значение статистики по формуле

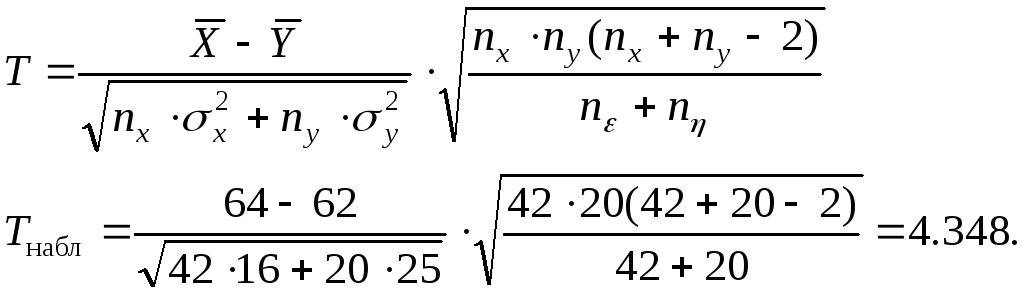
Критическая область для проверки гипотезы , при.

Значение t_кр= t_60;0.05 отыскиваем по таблице критических значений распределения Стьюдента, α в верхней строке: t_60;0.05=2,00. Т.к. , то основная гипотезаH₀ отвергается и принимается альтернативная гипотеза H₁.

Т.о., различие между ежедневным объемом продаж в Автозаводском и Центральном районах на 5% уровне значимости не существенно.