ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Поволжский государственный университет
Сервиса»
Кафедра: «Высшая математика »
Контрольная работа
По дисциплине: «Математика»
Работу выполнил
студент гр.
Проверил:
Тольятти 2012 г.
Содержание
Задача 1…………………………………………………………………….4
Задача 2…………………………………………………………………….5
Задача 3…………………………………………………………………….6-7
Задача 4…………………………………………………………………….8
Задача 5…………………………………………………………………….9
Задача 6……………………………………………………………………10
Задача 7……………………………………………………………………11-14
Задача 8……………………………………………………………………15
Задача 9……………………………………………………………………16-17
Задача 10…………………………………………………………………..18-21
Литература………………………………………………………………..22
Задача
1. В
ящике находятся
одинаковых пар перчаток черного цвета
и
одинаковых пар перчаток бежевого цвета.
Найти вероятность того, что две наудачу
извлеченные перчатки образуют пару.
Решение:
Рассмотрим:
событие A – две извлечённые наудачу перчатки образуют пару черного цвета;
событие В – две извлечённые наудачу перчатки образуют пару бежевого цвета.
P(A)
=
;
P(B)
=
.
Искомая вероятность:
P=P(A)
+ P(B)
=
или
P=
.
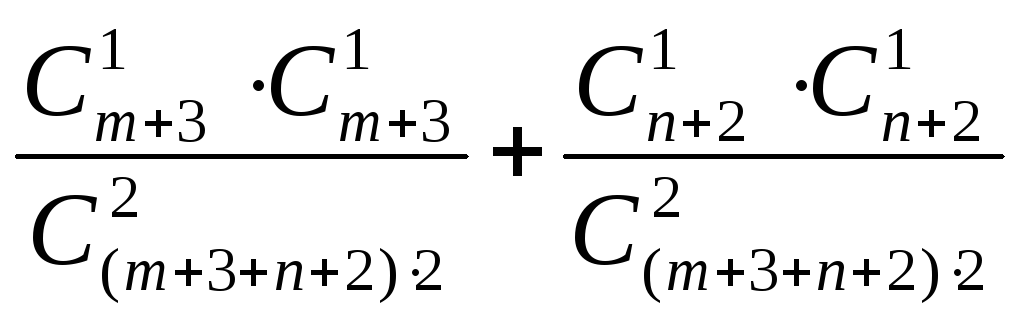Так
как
,
имеем:
P=
P(A) + P(B) =
.
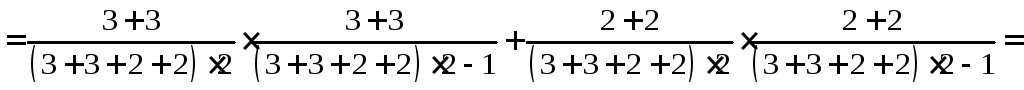
Ответ:
.
Задача
2. В урне
находятся 3 шара белого цвета и
шаров черного цвета. Шар наудачу
извлекается и возвращается в урну три
раза. Найти вероятность того, что среди
извлеченных шаров окажется:
а) ровно два белых шара;
б) не менее двух белых шаров.
Решение:
Рассмотрим
событие
– при
– ом извлечении достают белый шар.
P(A1)=
P(A2)=
P(A3)=
;
P
.
а)
вероятность
того, что среди извлеченных шаров
окажется ровно два белых шара:
P
=
.
б) вероятность того, что среди извлеченных шаров окажется не менее двух белых шаров:
P
=
.
Так
как
,
то текст задачи примет вид:
В урне находятся 3 шара белого цвета и 3 шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:
а) ровно два белых шара;
б) не менее двух белых шаров.
а)
P
=
б)
P
=
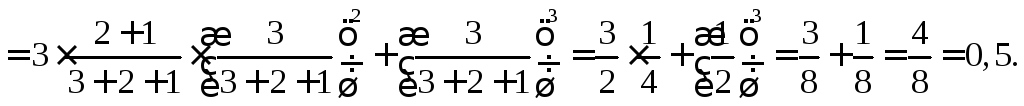
Ответ:
Задача
3. В урне
находятся
белых и
черных шара. Последовательно извлекаются
наудачу три шара без их возвращения в
урну. Найти вероятность того, что третий
по счету шар окажется белым.
Решение:
Рассмотрим
событие
– при
– ом извлечении достают белый шар.
; 
; 
;
;
;
;
;
;
.
По формуле полной вероятности:
Так
как
,
получаем задачу:
В урне находятся 5 белых и 4 черных шара. Последовательно извлекаются наудачу три шара без их возвращения в урну. Найти вероятность того, что третий по счету шар окажется белым.
;
;
;
;
;
;
;
;
;
.
По формуле полной вероятности:
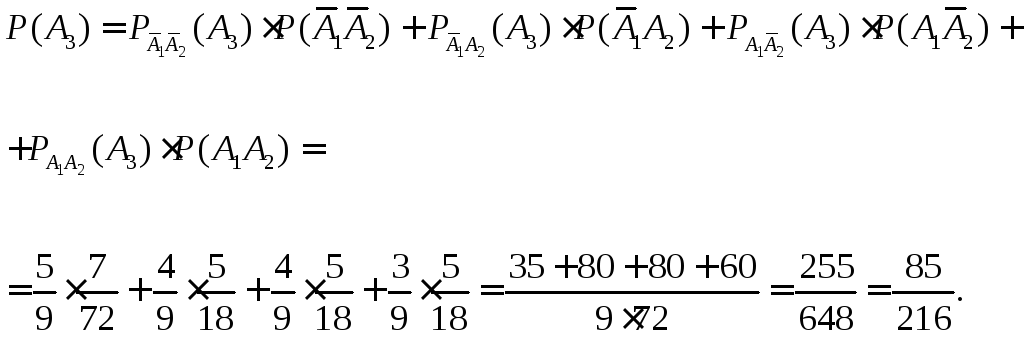
Ответ:
.
Задача
4.
Число деталей, выпущенных на первом
заводе, относится к числу деталей,
выпущенных на втором заводе как
.
Вероятность выпуска годной детали на
первом заводе равна 0,06, а для второго
завода эта вероятность равна 0,3. Все
детали поступают на один склад. Какова
вероятность того, что наугад взятая со
склада деталь будет годной?
Решение:
Пусть:
–гипотезы,
состоящие в выборе соответственно
детали, выпущенной на первом заводе и
на втором заводе;
событие
– наугад взятая со склада деталь будет
годной.
тогда:
;
;
-
(вероятность выпуска годной детали на
первом заводе);
-
(вероятность выпуска годной детали на
втором заводе).
Искомую вероятность найдем по формуле Бейеса:
Ответ:
.
Задача 5. Среди учебников 30% старых. Вероятность того, что в старом учебнике есть все темы лекционного курса, равна 0,8. В новых учебниках отражены все темы лекционного курса с вероятностью 0,52. Учебник содержит все темы лекционного курса. Какова вероятность того, что этот учебник новый?
Решение:
Пусть:
–гипотезы,
состоящие в выборе соответственно
старого и нового учебника;
событие
– учебник содержит все темы курса.
тогда:
;
;
-
(вероятность того, что в старом учебнике
есть все темы лекционного курса);
-
(вероятность того, что в новом учебнике
есть все темы лекционного курса).
Искомую вероятность найдем по формуле Бейеса:
Ответ:
.
Задача
6-4. Закон
распределения дискретной случайной
величины
имеет вид:
|
|
|
|
0 |
3 |
5 |
|
|
0,2 |
0,1 |
0,2 |
|
|
Найти
вероятности
,
дисперсию
,
если математическое ожидание равно:
.
Решение: