3.3. Свойства математического ожидания

1. Математическое ожидание постоянной равно ей самой

Случайная величина принимает только одно значение с с вероятностью 1. Тогда .

2. Константу можно выносить за знак математического ожидания

Случайные величины иотличаются значениями.

Поэтому .

3. Математическое ожидание суммы равно сумме математических ожиданий

Пусть задано совместное распределение случайных величин и:,.

Тогда

.

Разобьем на две суммы

.

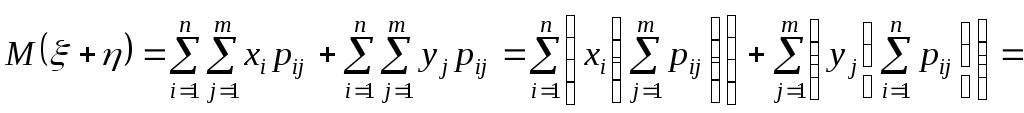
4. Математическое ожидание произведения независимыхслучайных величин равно произведению их математических ожиданий

Если случайные величины инезависимы, то.

Тогда

.

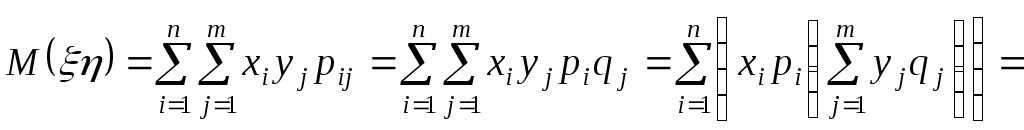
Математическое ожидание является числом. Поэтому для любых случайных величин ивыполняются равенства:

Пример 1. Дано. Найти.

Используем свойства 1, 2, 3.

Пример 2. Для случайной величинынайти.

Используем свойство 2.

.

Так как это число, то из свойства 1 следует

.

Тогда

Случайная величина называетсяцентрированной.

3.4. Дисперсия случайной величины и ее свойства. Среднеквадратическое отклонение

Считаем, что случайная величина имеет математическое ожидание.

Нас интересует разброс значений случайной величины относительно своего математического ожидания (среднего значения). Для любой случайной величины справедливо. Поэтому в качестве среднего отклонения относительноберут математическое ожидание случайной величины.

Дисперсиейслучайной величиныназывается число

Закон распределения случайной величины задан

.

Тогда

Если число значений бесконечно, то существует при сходимости ряда.

Число называетсясреднеквадратическим отклонениемслучайной величины. Используются и другие обозначения дисперсии

.

Рассмотрим свойства дисперсии.

1. Дисперсия константы равна нулю

Из свойства математического ожидания: . Тогда.

2. Дисперсия любой случайной величины неотрицательна:

При вычислении дисперсии суммируются неотрицательные числа:

где ипри.

Поэтому .

3. Константа выносится из-под знака дисперсии с квадратом

По определению дисперсии и свойствам математического ожидания

.

4. Сдвиг на константу не меняет дисперсию

Из свойства математического ожидания: . Тогда

.

5. Дисперсия случайной величины равна разности математического ожидания ее квадрата и квадрата математического ожидания самой случайной величины

.

В данном равенстве отбрасывают скобки

Приведем формулу вычисления математического ожидания квадрата дискретной случайной величины

где .

Используем свойства математического ожидания

.

6. Дисперсия суммы независимыхслучайных величин равна сумме их дисперсий

Приведем доказательство.

.

Далее пользуемся независимостью случайных величин

.

Пример 1. Задан закон распределения случайной величины

		0	2
	0,3	0,5	0,2

Найти .

Используем формулу .

Найдем :

.

Тогда

;

.

Пример 2. Задан закон распределения случайной величины

	3	4
	0,2	0,8

Найти среднеквадратическое отклонение . Используем формулу.

;

;

;

.

Пример 3. Случайные величиныХиYнезависимые и. Найти.

Используем свойства дисперсии:

.