3.2. Совместное распределение двух дискретных случайных величин. Некоторые арифметические операции над дискретными случайными величинами

Заданы законы распределения двух случайных величин:

Их суммойназывается случайная величина , значениями которой являются все возможные суммы . Определяются вероятности:

.

Произведениемэтих случайных величин является случайная величина , значениями которой являются все возможные произведения .

Определяются вероятности:

.

Событие состоит в том, что одновременно случайная величина принимает значение , а случайная величина - значение . Обозначим эту вероятность

.

Набор точек вместе с вероятностями образует совместное распределение случайных величин и .

Все пары должны быть учтены. Поэтому

.

Зная совместное распределение дискретных случайных величин и , можно восстановить закон распределения и .

Так как , то

.

Так как , то

.

Совместное распределение двух дискретных случайных величин удобно записывать с помощью таблицы

Две дискретные случайные величины называются независимыми, если события и при всех и независимы.

При независимости случайных величин и выполняются равенства:

, ; .

Пример 1. Задано совместное распределение случайных величин и .

		2	3
1	0,1	0,15	0,05	0,3
2	0,2	0,1	0,1	0,4
4	0,2	0,05	0,05	0,3
	0,5	0,3	0,2

1. Найти закон распределения случайных величин и .

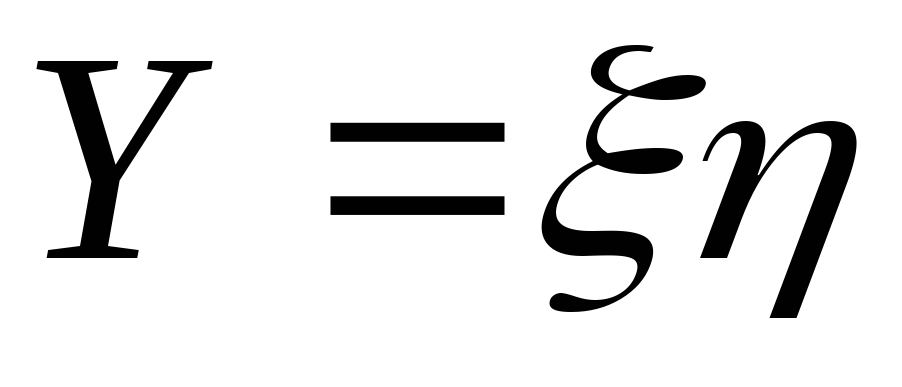2. Записать закон распределения случайных величин и 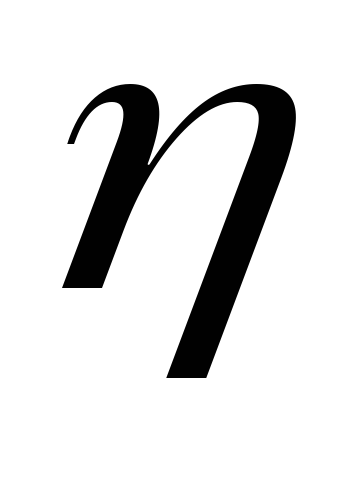и проверить их зависимость.

1) Найдем , где и , под ними подпишем соответствующие вероятности :

	0,1	0,15	0,05	0,2	0,1	0,1	0,2	0,05	0,05

При сложении получаются и равные суммы. Тогда

.

.

.

.

Закон распределения случайной величины :

	0	1	3	4	5	6	7
	0,1	0,2	0,35	0,15	0,1	0,05	0,05

Если бы нам нужно было найти только МХ, нам бы достаточно было воспользоваться предыдущей таблицей .

Найдем произведения , где , под ними подпишем вероятности :

	0,1	0,15	0,05	0,2	0,1	0,1	0,2	0,05	0,05

Одинаковых значений при вычислении произведений нет. Запишем закон распределения случайной величины :

				2	3	4	6	8	12
	0,2	0,2	0,1	0,15	0,05	0,1	0,1	0,05	0,05

2) Найдем вероятности принятия значений 1, 2, 4 случайной величиной :

.

Закон распределения случайной величины :

	1	2	4
	0,3	0,4	0,3

Суммирование по столбцам дает нам вероятности принятия значений , 2, 3 случайной величиной :

.

Закон распределения случайной величины :

		2	3
	0,5	0,3	0,2

Проверим равенства :

;

.

Тогда случайные величины и зависимые. Если бы , то мы перешли бы к проверке оставшихся равенств.