§ 8. Формула полной вероятности. Формула Байеса

Пусть события попарно несовместны и . Нам известны и , . Вероятность событияВнаходится по формуле

Эта формула носит название формулы полной вероятности. Докажем ее.

Разобьем событие Вна сумму несовместных событий. Вероятность суммы несовместных событий равна сумме вероятностей . Для каждого слагаемого используем формулу вероятности произведения событий , . Итак,

.

События называют еще предположениями. Все предположения должны быть выдвинуты и никакие два предположения одновременно происходить не могут.

Если событие Впроизошло, то с какой вероятностью происходит то или другое предположение ?

Эту вероятность легко получить, используя формулу полной вероятности и определение условной вероятности:

.

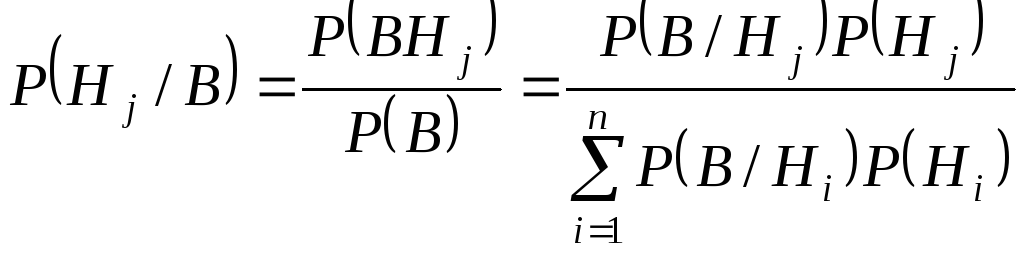Получена формула Байеса:

,

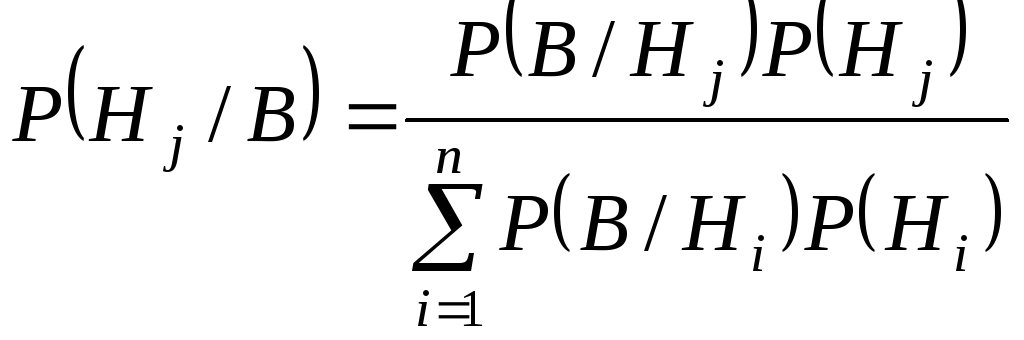где события несовместны и .

Пример 1. На склад поступают детали с двух цехов, причем с первого цеха поступает 40% деталей. Вероятность выпуска детали первого сорта в первом цехе равна 0,7, а для второго цеха эта вероятность 0,8. С какой вероятностью наугад взятая со склада деталь будет первого сорта?

Выдвинем предположения:

деталь выпущена в первом цехе,

деталь выпущена во втором цехе.

Из всех деталей 40% деталей выпускается в первом цехе. Тогда . Аналогично, находим вероятность того, что деталь выпущена во втором цехе .

Введем событие: деталь первого сорта.

Вероятность выпуска детали первого сорта в первом цехе .

Вероятность выпуска детали первого сорта во втором цехе .

Используем формулу полной вероятности

.

.

Пример 2. Наугад выбираем один из трех ящиков. В первом ящике 8 белых и 2 черных шара, во втором ящике 5 белых и 5 черных шаров, а в третьем ящике все белые. Наугад взятый шар из выбранного ящика оказался белым. С какой вероятностью это шар из второго ящика?

Наугад выбираем один из трех ящиков. Поэтому выдвигаем три предположения:

выбрали первый ящик;

выбрали второй ящик;

выбрали третий ящик.

Причем и слагаемые равны. Тогда .

Введем события: А– выбрали белый шар.

Вероятность взять белый шар, если в ящике 8 белых и 2 черных шара. Это условная вероятность .

Вероятность взять белый шар, если в ящике 5 белых и 5 черных шаров. Это условная вероятность .

Если в ящике все белые шары, то вероятность взять из него белый шар .

Найдем вероятность того, что шар взят из второго ящика, если вынутый шар белый . Используем формулу Байеса:

;

.

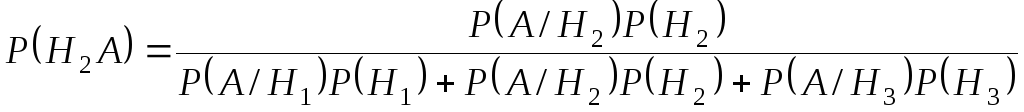Глава 2. Случайные величины

§ 1. Понятие случайной величины

Пусть задано вероятностное пространство . Каждому элементарному исходу ставится в соответствие число. То есть строится функция из множества элементарных исходов в множество действительных чисел. Определим множество, состоящее в том, что функция принимает значения меньше значения :

.

Для любого действительного значения хмножество является событием, т.е. . Функция называется случайной величиной.

Случайной величинойназывается функция, такая, что является событием при любом .

Событие принято обозначать и по-другому:

.

Случайные величины обозначают большими буквами Х,Y,Z, … или

Пример 1. Правильную монету подбрасывают дважды. Пространство элементарных исходов состоит из четырех элементов:

.

Все элементарные исходы происходят с равной вероятностью.

В качестве алгебры Fвозьмем множество подмножеств

.

Функция показывает число выпавших гербов при двух подбрасываниях монеты: .

Используем классическое определение вероятности:

;

;

.

Итак,

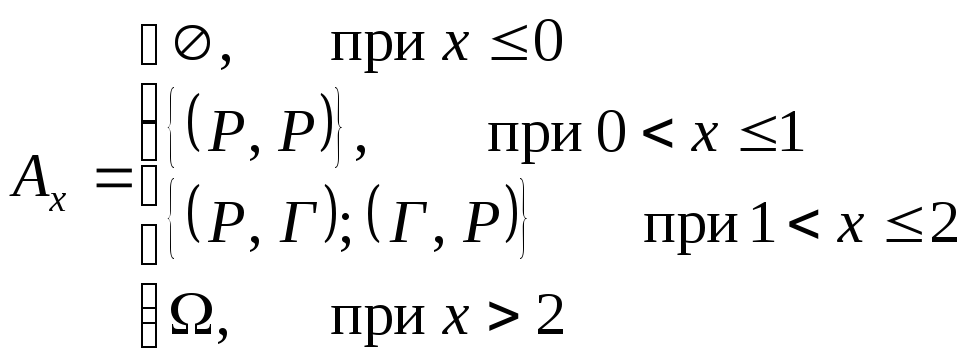
Для всех выполняется условие . Тогда функция является случайной величиной.