
- •Введение
- •Глава 1. Случайные события
- •§ 1. Случайные события
- •§ 2. Действия над событиями
- •§ 3. Элементарные события. Алгебра случайных событий
- •§ 4. Вероятность события
- •§ 5. Некоторые следствия из аксиом вероятности
- •§ 6. Классическое определение вероятности
- •§ 7. Условная вероятность. Независимость событий
- •§ 8. Формула полной вероятности. Формула Байеса
- •Глава 2. Случайные величины
- •§ 1. Понятие случайной величины
- •§ 2. Закон распределения дискретной случайной величины
- •§ 3. Числовые характеристики дискретных случайных величин
- •3.1. Математическое ожидание дискретной случайной величины
- •3.2. Совместное распределение двух дискретных случайных величин. Некоторые арифметические операции над дискретными случайными величинами
- •3.3. Свойства математического ожидания
- •3.4. Дисперсия случайной величины и ее свойства. Среднеквадратическое отклонение
- •3.5. Мода и медиана дискретной случайной величины
- •3.6. Корреляционный момент. Коэффициент корреляции
- •3.7. Моменты дискретных случайных величин
- •3.8. Функция распределения
- •§ 4. Непрерывные случайные величины
- •4.1. Плотность распределения, функция распределения непрерывной случайной величины
- •4.2. Характеристики непрерывных случайных величин
- •§ 5. Некоторые специальные виды распределений
- •5.1. Гипергеометрическое распределение
- •5.2. Биномиальное распределение
- •5.3. Закон Пуассона
- •5.4. Равномерное распределение
- •5.5. Нормальное распределение
- •5.6. Некоторые важные статистические распределения
- •§ 6. Некоторые предельные теоремы теории вероятностей
- •6.1. Неравенство Чебышева
- •6.2. Закон больших чисел
- •6.3. Центральная предельная теорема. Интегральная и локальная теоремы Мувра-Лапласа
- •Приложение 1 Комбинаторика
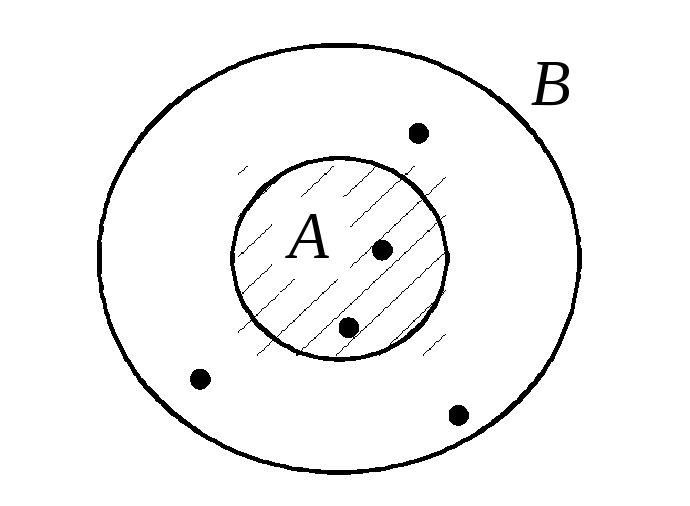
§ 5. Некоторые следствия из аксиом вероятности
Следствие 1. Вероятность любого события принадлежит отрезку от нуля до единицы:
![]()
Доказательство.
Достоверное событие ![]() является следствием любого события А,
и А
является следствием невозможного
события
является следствием любого события А,
и А
является следствием невозможного
события ![]() :
:
![]() .
.
Из аксиомы 2 имеем
![]() .
Используем аксиому 1, тогда
.
Используем аксиому 1, тогда ![]() .
.
Следствие 2. Вероятность того, что событие А не произойдет, равна единице минус вероятность того, что событие А произойдет:
![]()
Доказательство.
События А
и ![]() несовместны, в сумме образуют достоверное
событие:
несовместны, в сумме образуют достоверное
событие:
![]() и
и ![]() .
.
Тогда ![]() .
Из аксиом 1 и 2 вытекает
.
Из аксиом 1 и 2 вытекает ![]() ,
то есть
,
то есть ![]() .
.
Следствие 3. Вероятность того, что произойдет хотя бы одно из событий А и В, равна сумме вероятностей этих событий минус вероятность того, что эти события произойдут одновременно:
![]()
Доказательство.
Событие А
имеет место, если одновременно произойдут
события А
и В
или А и
![]() :
:
![]() .
.
Слагаемые являются несовместными событиями. Из аксиомы 3 следует:
![]() .
.
Аналогично, имеет место следующее равенство:
![]() и
и ![]() .
.
Хотя бы одно из двух событий имеет место, если произойдет только одно из них или оба события одновременно:
![]() .
.
Слагаемые являются попарно несовместными событиями. Из аксиомы 3 следует:
![]() .
.
Учитывая разложения
![]() и
и ![]() ,
имеем:
,
имеем:
![]() .
.
§ 6. Классическое определение вероятности
Рассматривается случайный эксперимент, исходы которого описываются конечным числом элементарных событий
![]() .
.
Всего п элементарных исходов. Каждый элементарный исход происходит с равной вероятностью
![]() .
.
Говорят, что элементарные исходы равновозможны.
Элементарный исход
![]() считается благоприятным для события
А,
если это событие является следствием
элементарного исхода
считается благоприятным для события
А,
если это событие является следствием
элементарного исхода ![]() :
:
![]() благоприятный
для А
исход
благоприятный
для А
исход
Дадим классическое определение вероятности.
Вероятностью
![]() события А называется отношение числа
благоприятных исходов к общему числу
элементарных исходов.
события А называется отношение числа
благоприятных исходов к общему числу
элементарных исходов.
Число благоприятных
исходов события А
обозначается ![]() .
Общее число элементарных исходов
обозначим
.
Общее число элементарных исходов
обозначим ![]() .
Тогда
.
Тогда
![]()
Проверим выполнение аксиом вероятности.
Невозможное событие не содержит ни одного элементарного исхода
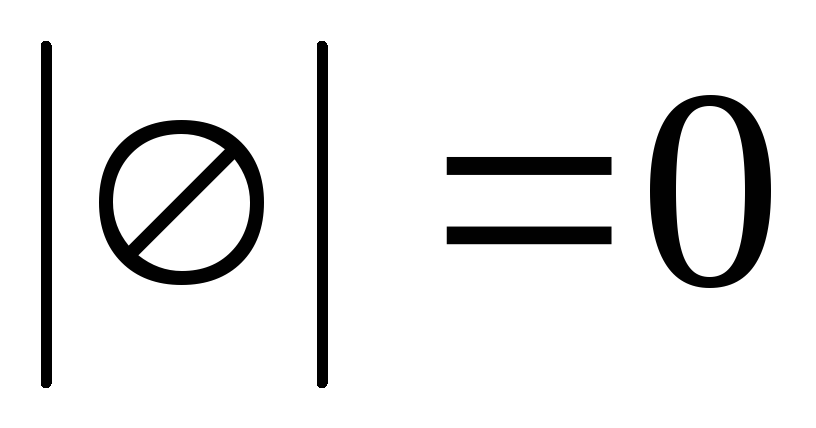 и
и 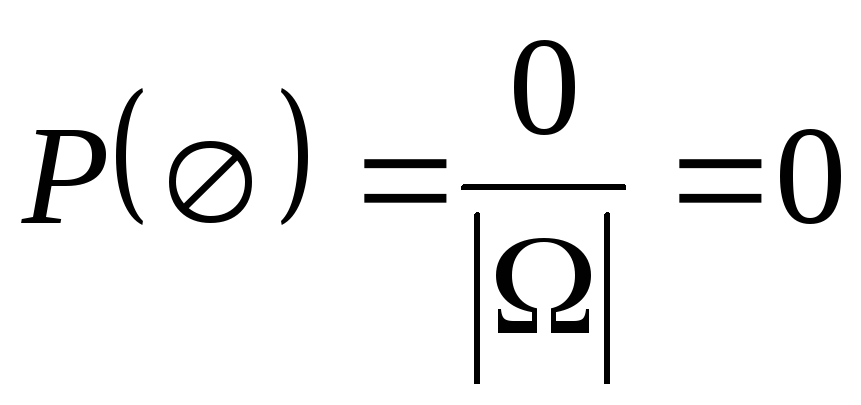 .
Достоверное событие содержит все
элементарные исходы и
.
Достоверное событие содержит все
элементарные исходы и 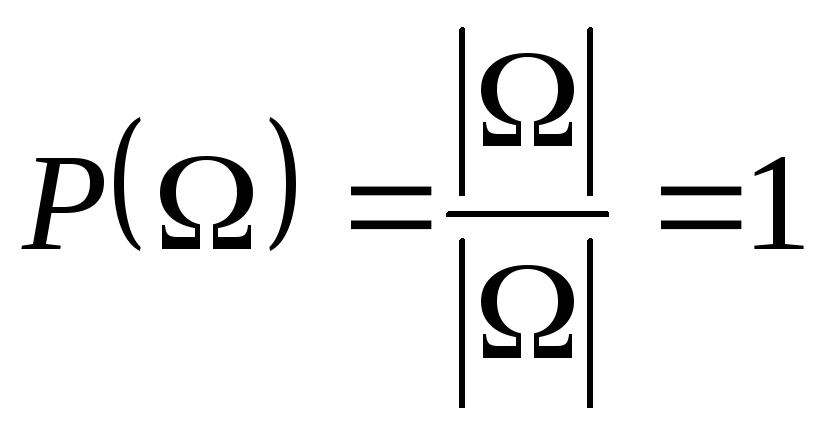 .
.Если
 ,
то
,
то  и
и 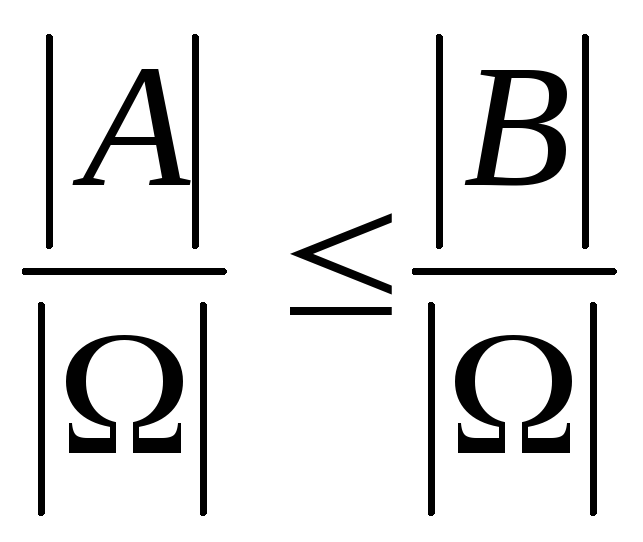 .
Тогда
.
Тогда 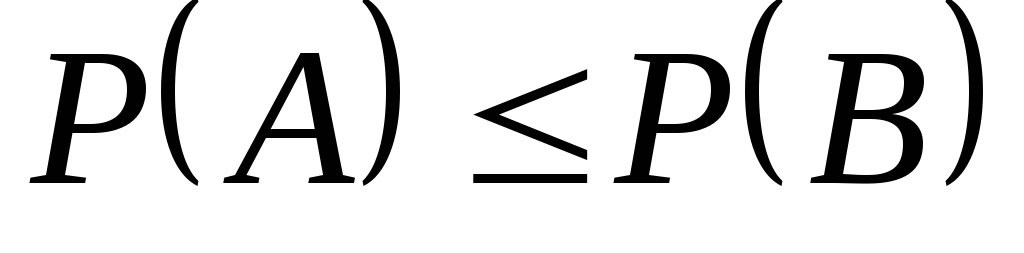 .
.
События А и В несовместные, тогда они не содержат одинаковых элементарных исходов. Следовательно,
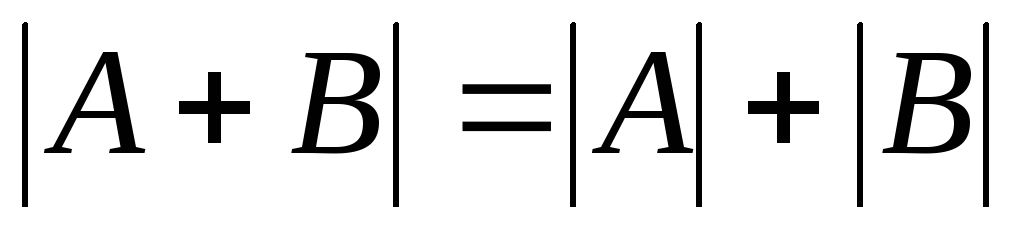 и
и 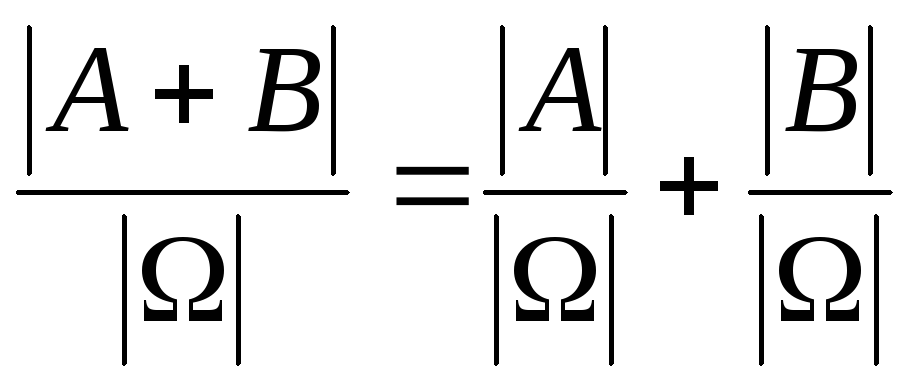 .
И
.
И 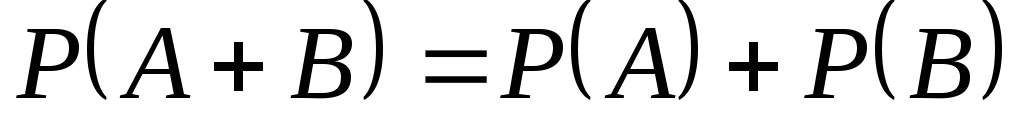 .
.
Классическое определение вероятности является частным случаем аксиоматического определения.
Пример 1. Подбрасывается правильная монета. С какой вероятностью выпадет решка?
Пространство
элементарных исходов состоит из двух
элементов
![]() .
.
Событие А–
выпала решка – имеет один благоприятный
исходР. Тогда
![]() .
.
Пример 2. В урне 5 белых и 2 черных шара, наугад вынимаем один шар. С какой вероятностью будет вынут белый шар?
При построении пространства элементарных исходов нужно учесть число шаров каждого вида.
Введем события:
![]() взяли
i-й белый шар,
взяли
i-й белый шар,
![]() ;
;
![]() взяли
i-й черный шар,
взяли
i-й черный шар,
![]() .
.
Тогда
![]() и
и
![]() .
.
Событие В–
взяли белый шар. Для него
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
В каждом примере с учетом проводимого опыта строится пространство элементарных исходов.
Пример 3. В урне 5 белых и 2 черных шара. Наугад выбираем три шара. С какой вероятность среди выбранных шаров будет один черный?
В чем состоит опыт?
Из семи шаров выбираем три, порядок
выбора роли не играет. Тогда пространство
элементарных исходов состоит из сочетаний
из семи по три
![]() .
.
Нас интересует
событие В– из трех выбранных два
белых шара и один – черный. Из пяти белых
выбираем два, это можно сделать
![]() способами. Из двух черных шаров можно
выбрать один двумя способами. Каждый
черный шар мы должны взять с каждой
парой белых шаров, поэтому
способами. Из двух черных шаров можно
выбрать один двумя способами. Каждый
черный шар мы должны взять с каждой
парой белых шаров, поэтому
![]() и
и
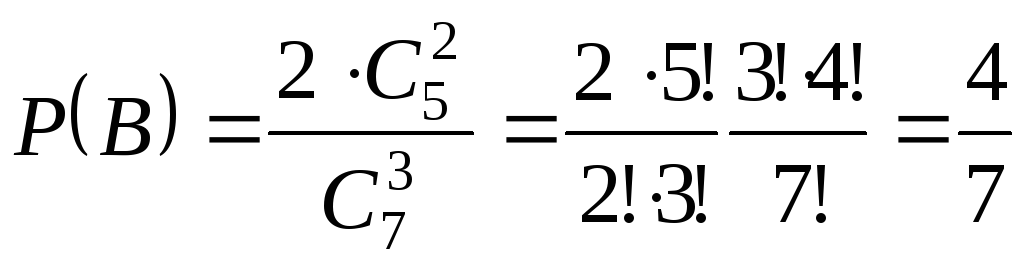 .
.
