6.3. Центральная предельная теорема. Интегральная и локальная теоремы Мувра-Лапласа

Центральная предельная теорема. Пусть случайные величинынезависимы, одинаково распределенные с математическим ожиданиемаи конечной дисперсией. Тогда при большихп

.

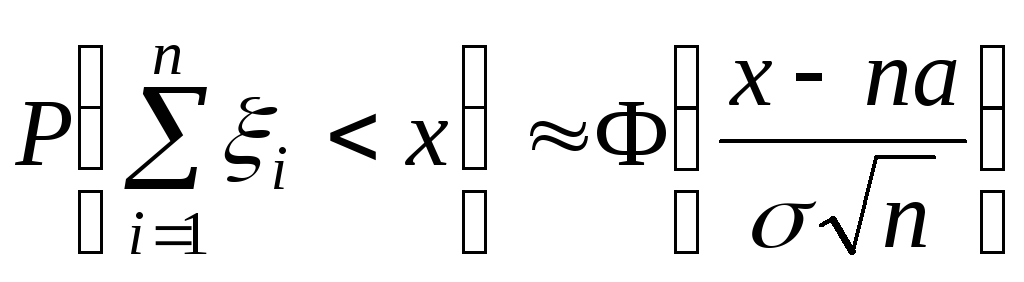То есть, если случайная величина представлена в виде суммы очень большого числа взаимно независмых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, тоимеет распределение, близкое к нормальному.

Частным случаем приведенного утверждения является интегральная теорема Муавра-Лапласа.

Теорема Муавра-Лапласа. Случайная величинабиномиально распределена с параметрамипир. Тогда

.

Биномиально распределенная случайная величина показывает, сколько раз событиеАпроизошло средипнезависимых одинаковых опытов, в каждом из которых событиеАможет прозойти с вероятностьюри не произойти с вероятностью.

Случайная величина представляется в виде суммы независимых случайных величин, для которых.

Напомним, что , если вi-м испытании произошло событиеА, и, если вi-м испытании событиеАне произошло. Мы знаем значения основных характеристик слагаемых

.

Приведем соответствие обозначений для данной случайной величина в приведенной выше центральной предельной теоремеи. Тогда

.

Вероятность того, что в пнезависимых одинаковых испытаниях, в каждом из которых вероятность появления событияАравнар, событиеАнаступит не менеераз и не болеераз обозначается. Тогда

.

Приведем еще одну теорему.

Локальная теорема Муавра-Лапласа. Вероятность того, что впнезависимых одинаковых испытаниях, в каждом из которых событиеАможет произойти с вероятностьюр, событиеАнаступит ровноkраз, приближенно равна

, где

Приближенное равенство имеет место при достаточно больших значениях п.

Пример 1. Найти вероятность того, что из 50 подбрасываний правильной монеты решка выпадет ровно 25 раз.

Монета правильная, поэтому вероятность появления решки равна 0,5: . Так как число проведенных подбрасываний (испытаний) велико, используем локальную теорему Муавра-Лапласа

; .

Используем таблицу значений функции Лапласа

и .

Пример 2. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что из 100 новорожденных мальчиков будет более 40, но менее 60.

Число родившихся мальчиков опысывается биномиально распределенной случайной величиной с параметрами . Используем интегральную теорему Муавра-Лапласа

.

.

Используем таблицу значений интеграла Лапласа

Тогда

.

Приложение 1 Комбинаторика

Приведем два правила, которые часто применяются при решении кобинаторных задач.

Правило 1. Пусть требуется выполнить одно за другимkдействий. Действие с номеромiможно выполнитьспособами,. Всеkдействий можно выполнитьспособами.

Правило 2. Пусть требуется выполнить два действия. Причем действия взаимно исключают друг друга, первое действие можно сделатьспособами, второе –способами. Тогда выполнить любое из действий можноспособами.

Пример 1. Имеется 5 красных и 4 зеленых шара. Составляется набор из трех шаров, один из которых – зеленый. Сколькими способами можно составить такой набор?

Красные шары выбираем из 5 красных. Первый красный шар выбирается из 5, а второй – из оставшихся 4. Тогда два красных шара выбираем способами. Каждую пару красных шаров нужно взять с каждым зеленым шаром. Тройку шаров можно составитьспособами.

Пример 2. На складе 10 деталей первого сорта и 6 – второго. Сколькими способами можно выбрать три детали, чтобы среди них были детали только одного сорта?

Из 10 деталей первого сорта выбираем три. Можно считать, что мы последовательно берем три детали. Первую деталь выбираем из 10. Вторую деталь выбираем из оставшихся 9. Из оставшихся 8 берем третью деталь. Тогда из 10 деталей первого сорта можно выбрать три способами. Аналогично из 5 деталей второго сорта можно выбрать триспособами. Выбираются три детали либо первого сорта, либо второго сорта. Тогда всеготребуемых способов.

Введем понятия размещений, перстановок и сочетаний.

Пусть имеется множество, содержащее пчисел. Все элементы множества можно перенумеровать, то есть каждому элементу множества поставть в соответствие число. Получаем последовательность элементов множества. Такие последовательности называютсяупорядоченными. Если в упорядоченном множестве поменять местами хотя бы два элемента, то получим новое упорядоченное множество.

Размещениемизпэлементов потназывается любое упорядоченное подмножество изтэлементов множества, состоящего изпразличных элементов.

Пример 3. Записать размещения по 2 элемента из 3 элементов множества.

На первое место ставим любой элемент множества. Из оставшихся двух элементов ставим любой на второе место.

Размещения

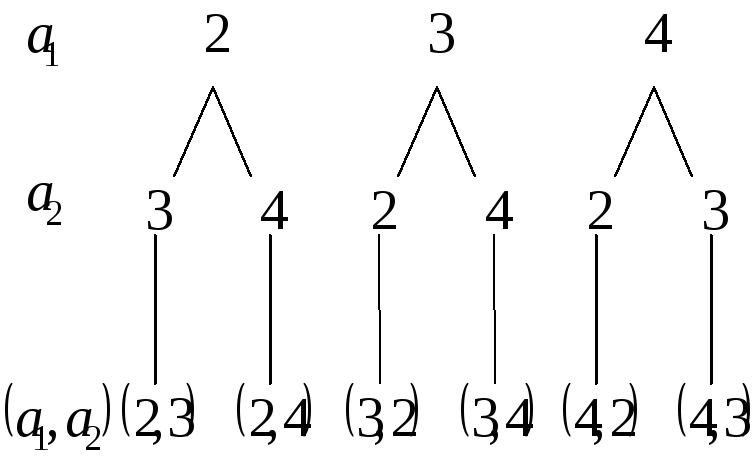
Чаще всего нам нужно знать не множество всех размещений, а их число. Число размещений из пэлементов потобозначается. Если, тотэлементов изпнельзя выбрать. Поэтомупри.

Число размещений из пэлементов потэлементов равно:

Мы составляем упорядоченное множество элементов множества. Из всего множества выбираем один и ставим его на первое место упорядоченного множества. Это можно сделатьпспоосбами, так как всегопэлементов. Остаетсяэлемент, из них выбираем в ролиодин элемент. Тогда заполнить первые два места упорядоченного множества можноспособами. Элементвыбирается изоставшегося элемента. Получить последовательностьможноспособами. Поэтому число размещений из множествапэлементов потэлементов равноспособам.

Используем понятие пфакториал:

Принято считать . Тогда

.

Мы доказали, что при.

Размещение из пэлементов попназываетсяперестановкой. Если все элементы множества записать в определенном порядке, то мы получаем перестановку.

Число перестановок из п элементов равно , так как.

Пример 4. Запишем все перестановки множества.

.

Из множества п элементов выбираем подмножества т элементов, причем порядок выбора роли не играет. Тогда мы получаемсочетание. Число сочетаний изпэлементов потобозначается. Сочетания между собой различаются только набором элементов. Из каждого сочетания можно получитьразмещений. Тогда. Итак,

при .

Пример 5. Запишем все сочетания по 2 из множества.

.

Из каждого сочетания можно получить по два размещения:

Сочетания
Размещения

Запишем некоторые свойства числа сочетаний:

1. .

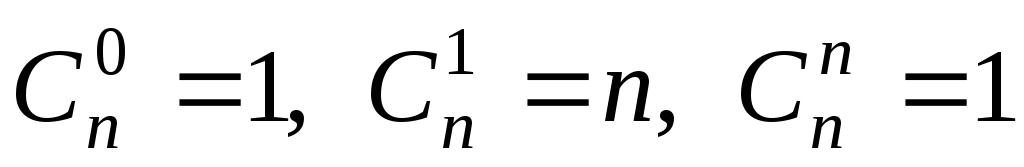Действительно:

.

2. .

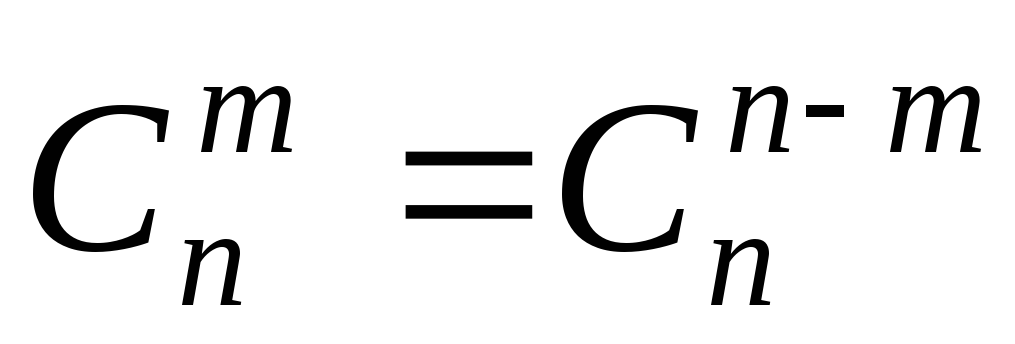Действительно:

и .

3. .

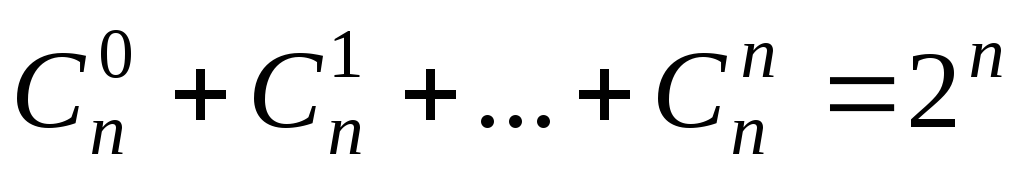Равенство вытекает из формулы бинома Ньютона

.

При

.

66