5.5. Нормальное распределение

Случайная величина имеетнормальное распределение(распределена по нормальному закону) с параметрамиаи, если она имеет плотность распределения

.

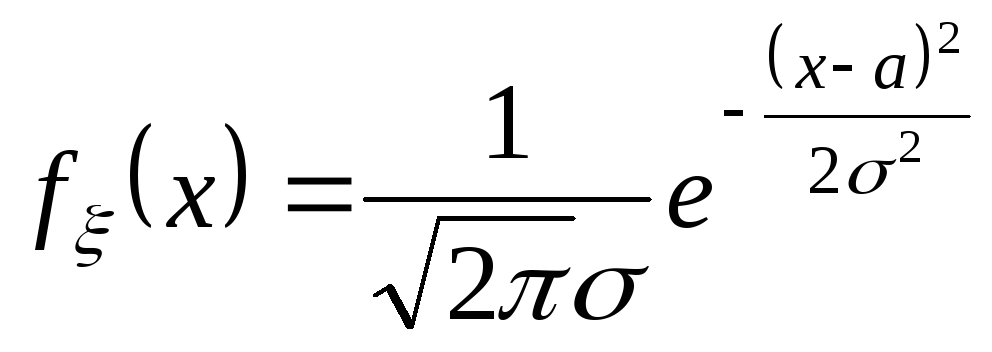Приведем график плотности распределения

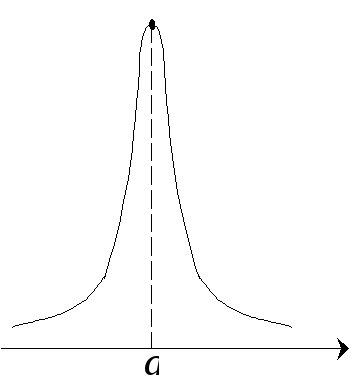
Запишем основные особенности функции :

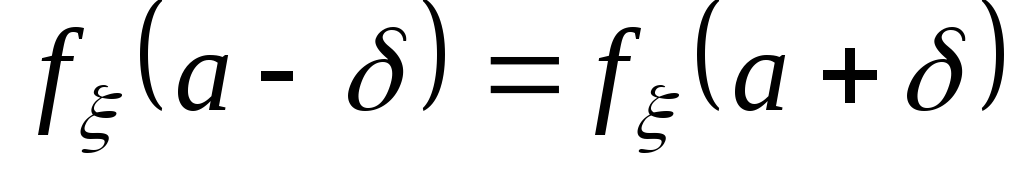1. ; при , график симметричен относительно прямой.

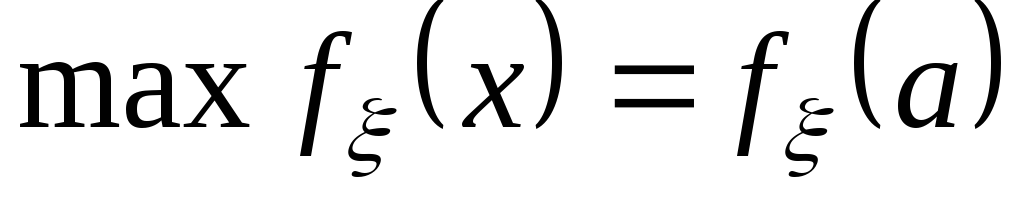2. ; наибольшее значение функции 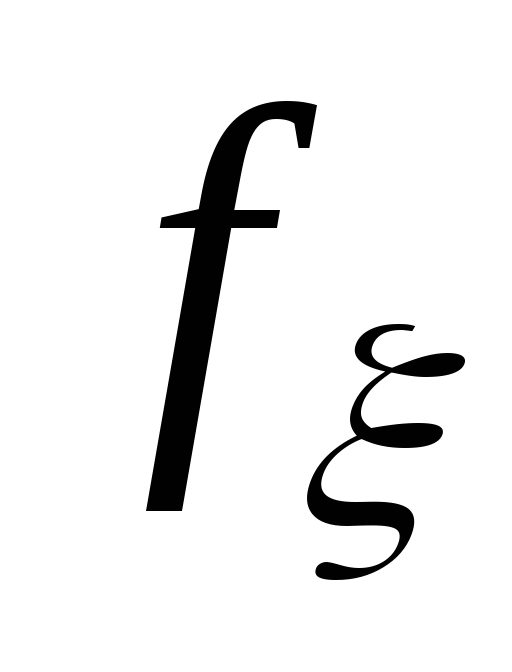достигается в точке.

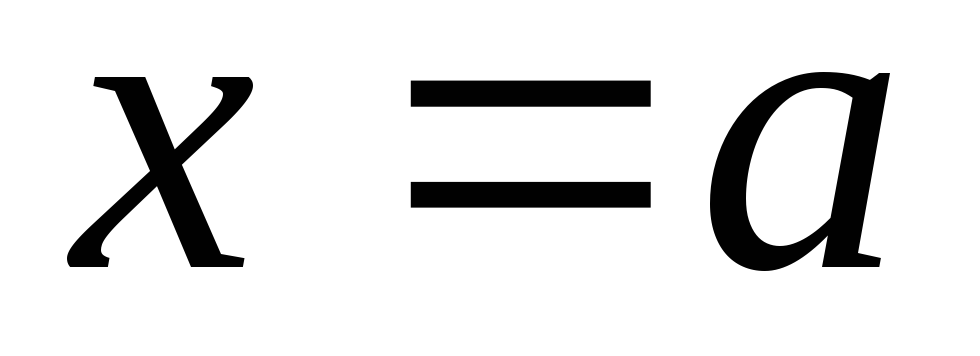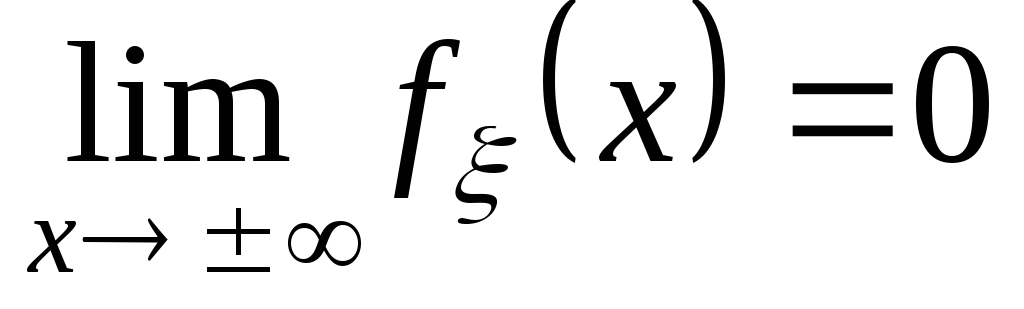3. , т.е. 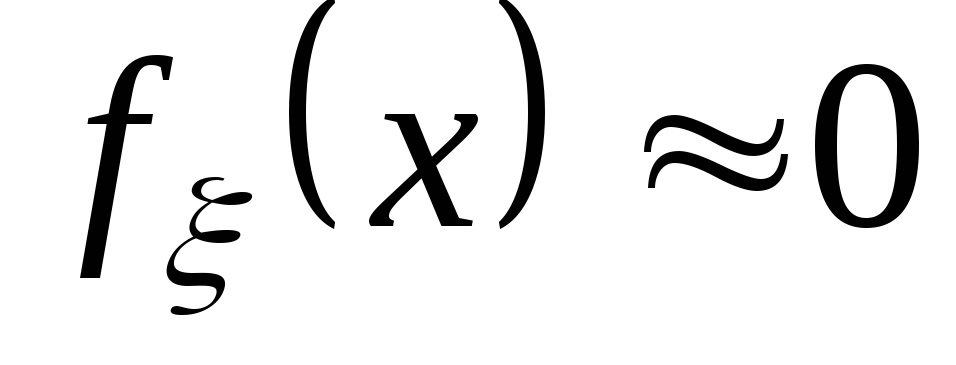при достаточно больших значенияхх.

Подграфик плотности распределения равен единице. Тогда из-за симметрии графика плотности распределения относительно прямой медиана нормально распределенной случайной величины равна параметруа

Из определения моды и свойства 2 следует, что и мода нормально распределенной случайной величины равна а

Нарисуем графики плотностей распределения при зафиксированном значении параметра аи разных

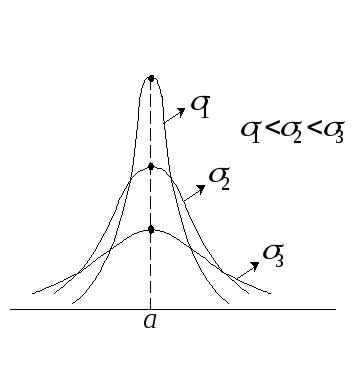
При меньших значениях график имеет более высокую вершину и круче падает к нулю. При малых значенияхвероятность принятия значения, далекие ота, мала. Параметрвлияет на разброс значений.

Из определения математического ожидания следует, что

.

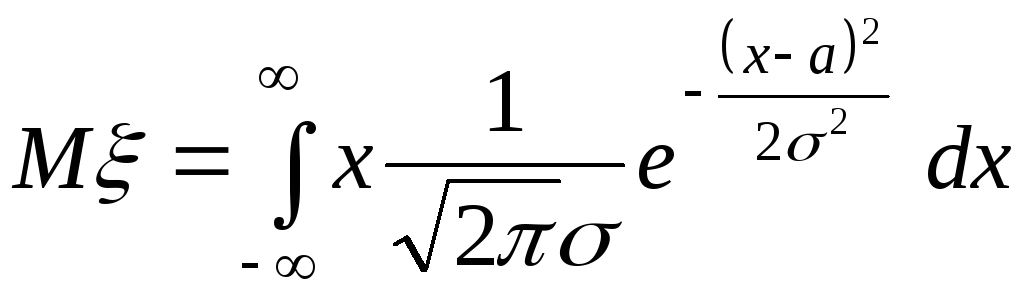Для вычисления этого интеграла делают замену и используют известный несобственный интеграл

.

Для нормально распределенной случайной величины с параметрамиаиматематическое ожидание равноа

Вычисление соответствующего интеграла дает нам дисперсию нормально распределенной случайной величины

Поэтому параметр является среднеквадратическим отклонением нормально распределенной случайной величины.

По плотности распределения находится функция распределения нормальной случайной величины

.

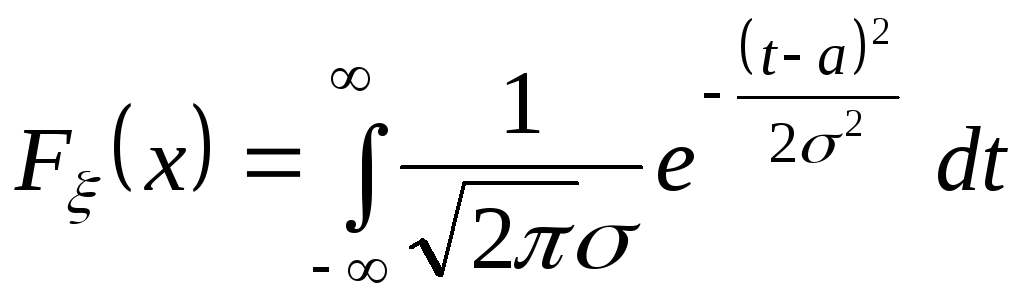Нормальное распределение с параметрами называютстандартным. Вводятся специальные обозначения плотности и функции распределения стандартно нормально распределенной случайной величины

Функцию называют еще функцией Лапласа.

Функция выражается через интеграл Лапласа

.

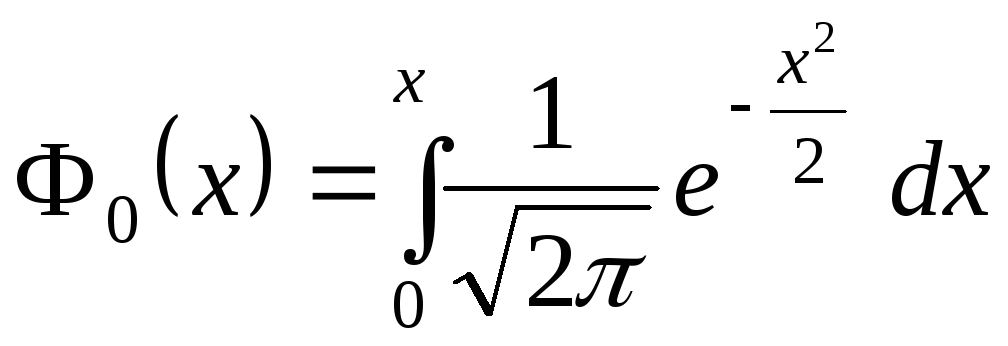Значения функции занесены в таблицу. При. Рассмотрим график плотности распределения стандартного нормального закона

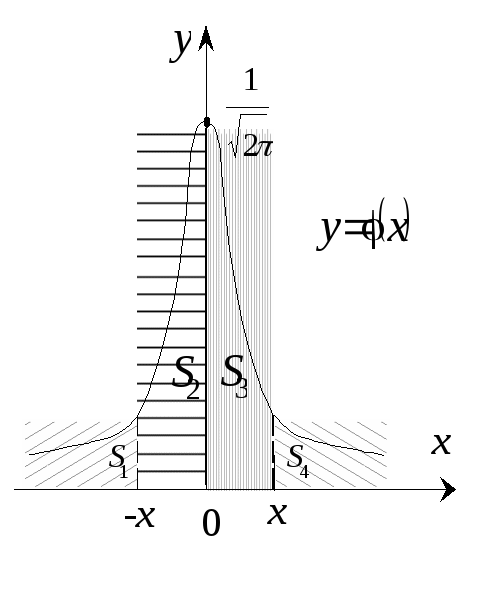
(значение хбольше нуля).

Обозначим площадь под левее точкичерез; площадь междуи 0 – через; площадь между 0 их– черези площадь правее точких– через. График плотности распределениясимметричен относительно прямой. Тогда

1. ;

2. ;

3. ;

4. .

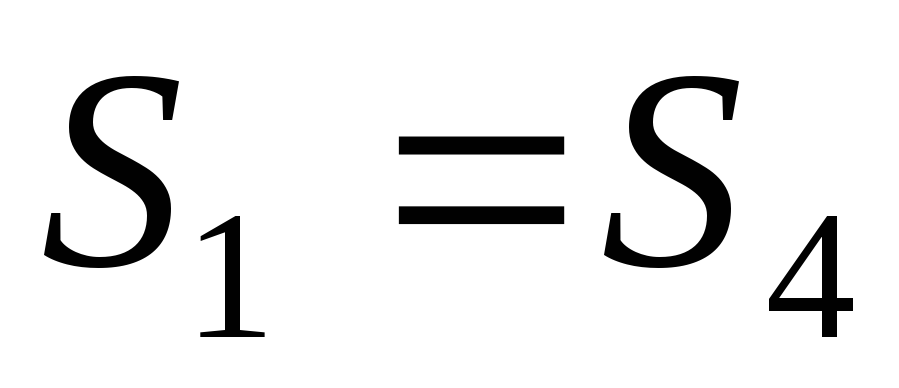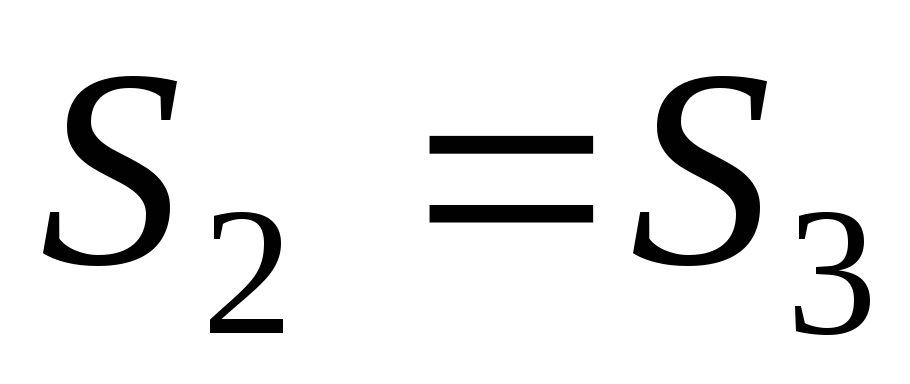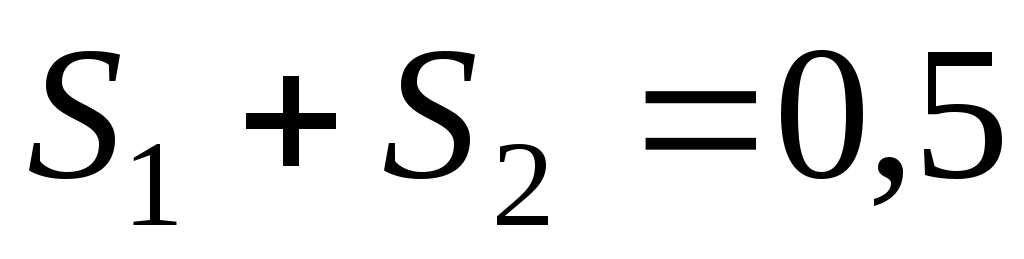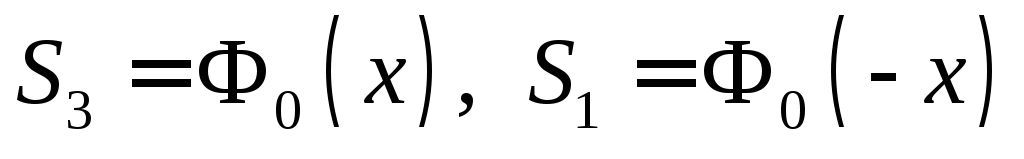Значение есть площадь подграфиканад множеством.

Если , то. Тогда

Из замечаний 1, 3, 4 следует . Тогда

Если случайная величина распределена по нормальному закону с параметрами а и, то случайная величинараспределена по стандартному нормальному закону.

Докажем это утверждение.

Рассмотрим функцию распределения случайной величины

.

Сделаем замену . Тогдаприипри.

Получаем

.

Тогда случайная величина распределена по стандартному нормальному закону.

Из доказательства следует связь между функцией распределения нормально распределенной случайной величины с параметрамиаии функцией распределения стандартного нормального закона

Тогда выражается вероятность попадания случайной величины в отрезок

.

Если отрезок симметричен относительно параметра а(математического ожидания), то приимеем

.

Тогда

.

Если взять , то

.

Итак, с вероятностью примерно 0,9974 значения нормальной случайной величины распределены в промежутке от до. Это свойство называетсяправилом трех сигм. Еще раз запишем это правило:

Практически все значения нормальной случайной величины находятся в промежутке .

Пример 1. Случайная величинараспределена нормально, причем. Записать плотность распределения случайной величины. Найти.

Определим параметры распределения случайной величины

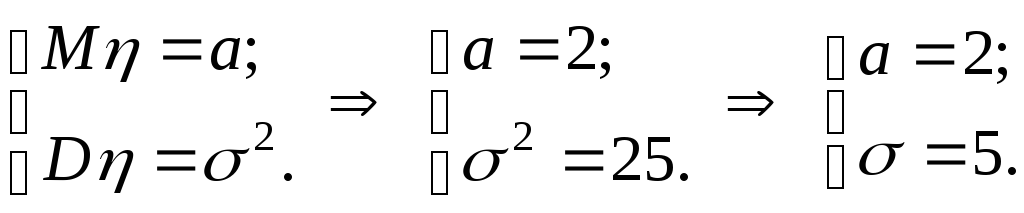
Запишем плотность распределения

.

Выразим функцию распределения нормально распределенной случайной величины через функцию распределения стандартно нормально распределенной случайной величины

.

Тогда

.

Пример 2. Случайная величиназадана плотностью распределения

.

Найти .

По виду плотности распределения заключаем, что случайная величинанормально распределена с параметрамии. Тогда.

Следовательно,

.

Пример 3. Случайная величинаХраспределена нормально с математическим ожиданием. Вероятность попаданияХв интервалравна 0,4. Чему равна вероятность попаданияХв интервал?

Так как график плотности распределения нормально распределенной случайной величинысимметричен относительно прямой,Х, то площади подграфиканад множествамииравны между собой.

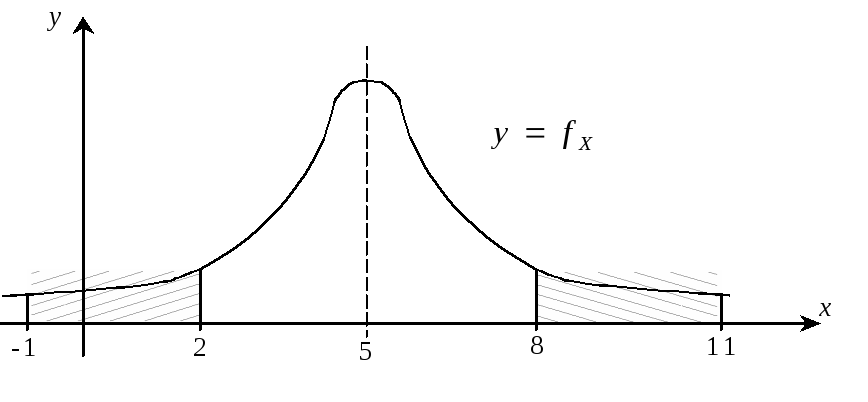
Тогда .

Пример 4. Случайная величинараспределена нормально с математическим ожиданием 3 и среднеквадратичем отклонением. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9438 попадает.

Воспользуемся формулой

.

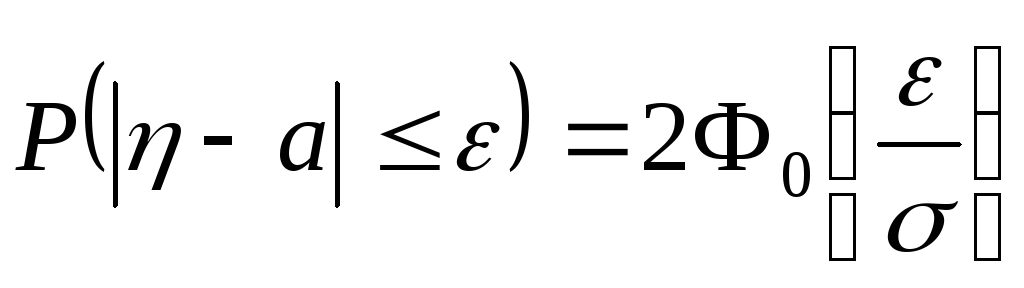При иимеем

.

По условию задачи . Тогда. По таблице значений интеграла Лапласа. Тогда,. Из неравенстваполучаем требуемый интервал.