5.3. Закон Пуассона

Случайная величина принимает целые не отрицательные значения и

где . Тогда говорят, что случайная величинараспределена по закону Пуассона с параметром а.

Выполняется условие

.

Действительно, вспомним разложение в ряд Маклорена функции

.

Тогда

.

Найдем основные характеристики случайной величины, распределенной по закону Пуасона с параметром а

1. 

По определению математического ожидания

.

Сделаем замену :

.

2. 

Найдем начальный момент второго порядка

.

Проведем замену

.

Тогда и.

3. Мода случайной величины, распределенной по закону Пуассона с параметром а, принадлежит отрезку

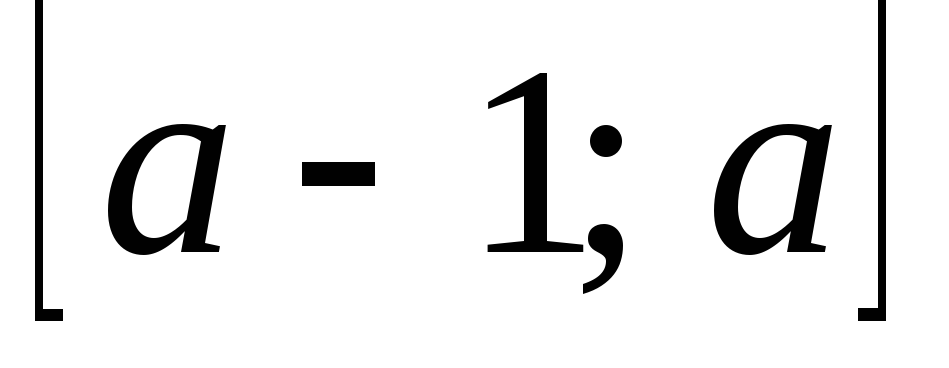
и целое.

Из определения моды

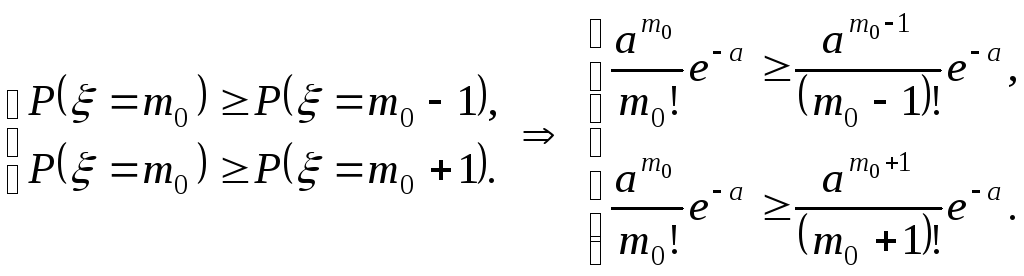
Используем соотношения и:

.

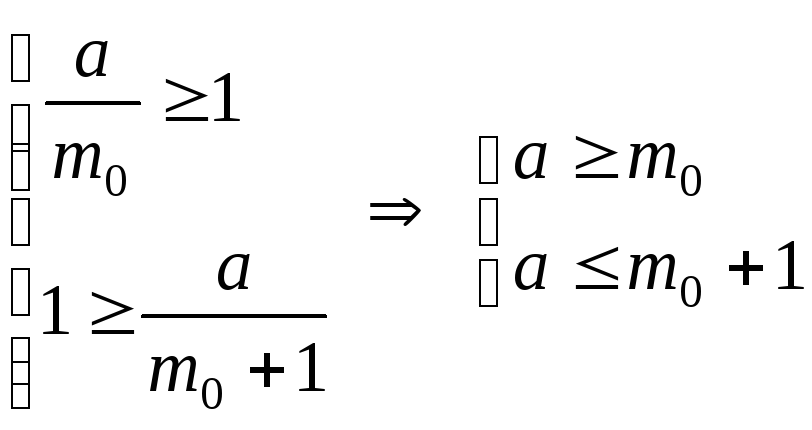Тогда .

Закон Пуассона является предельным для биномиального распределения.

Теорема Пуассона. Если вероятностьрнаступления событияАв каждом испытании постоянна и мала, а число независимых испытанийпдостаточно велико, то вероятность того, что событиеАнаступитkраз, приближенно равнагде.

.

Проведем доказательство. Разделим и домножим на

.

Используем условия и известные пределы:

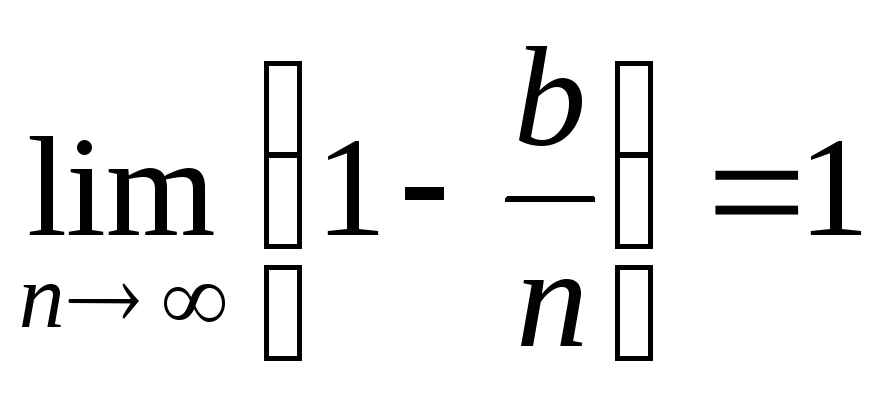1. при ;

2. ;

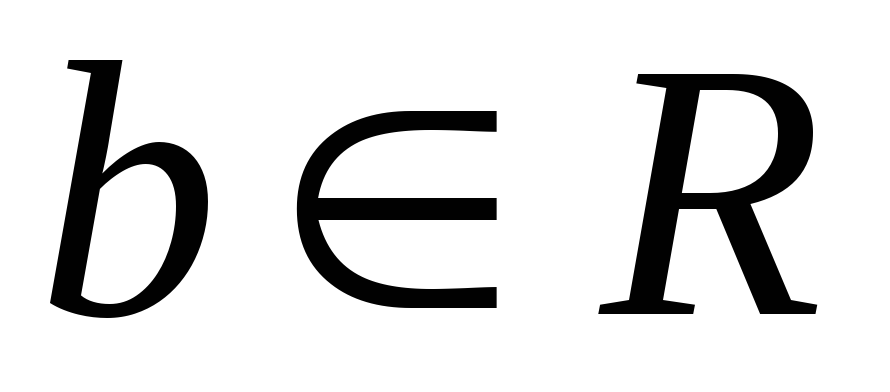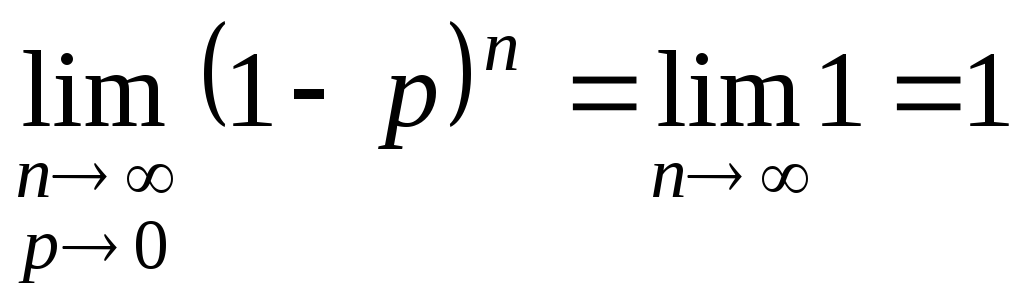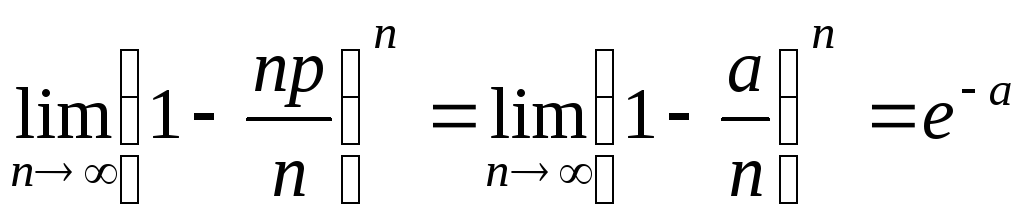3. в силу замечательного предела.

Тогда при ,иимеем

.

Пример 1. Случайная величинараспределена по закону Пуассона с параметром. Найти.

1. ;

2. ;

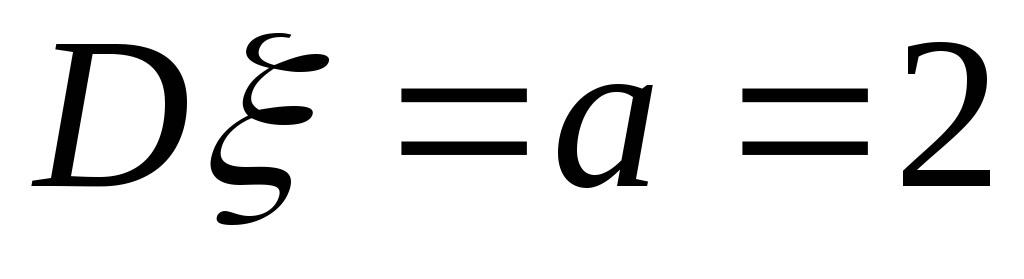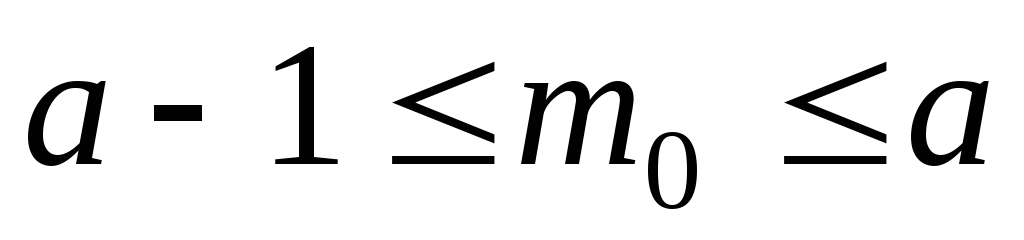3. . Тогда 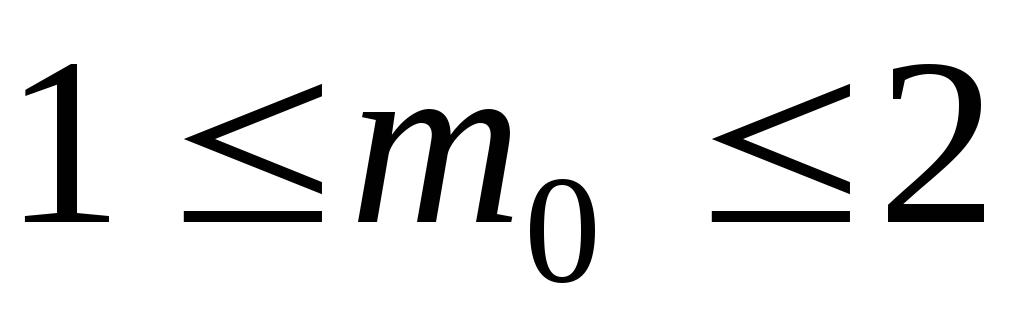. Так как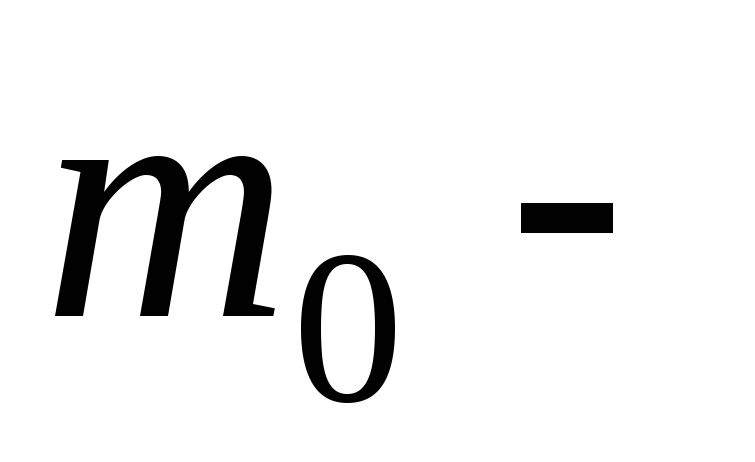целое, то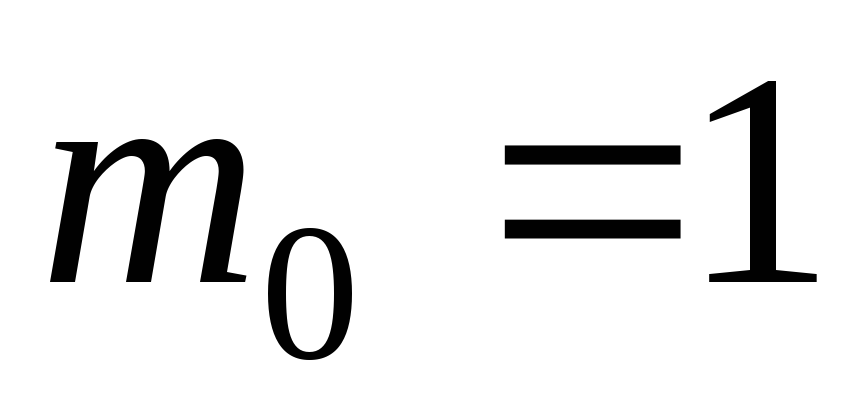и;

4. 

.

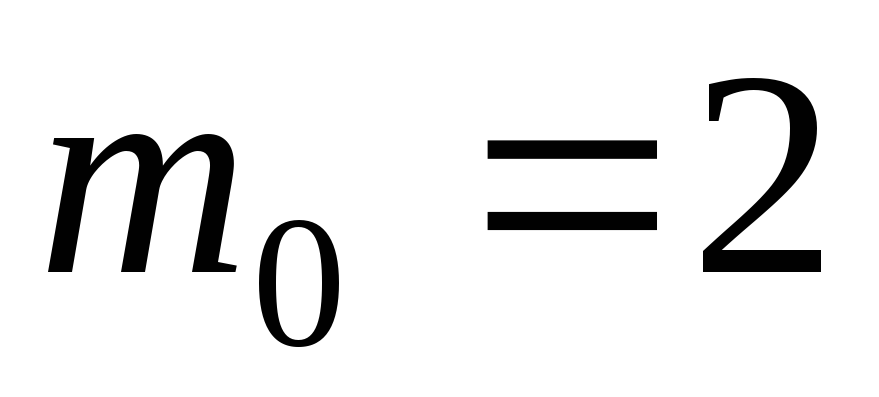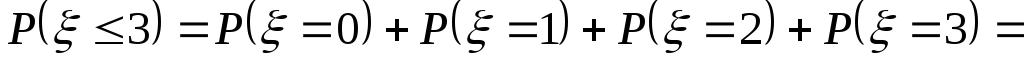
Значения задаются в таблице, их можно вычислить самим:

.

Пример 2. Вероятность выпуска бракованной детали равна 0,001. Какова вероятность того, что из 1000 деталей бракованных будет четыре.

Дано . Находим.

Воспользуемся теоремой Пуассона

.

5.4. Равномерное распределение

Случайная величина равномерно распределенана отрезке, если её плотность распределения имеет вид:

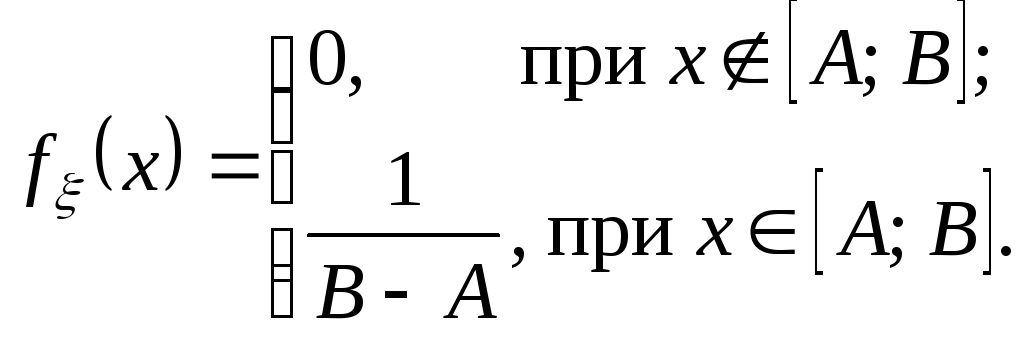
Значения АиВявляются параметрами распределения.

Плотность распределения равномерно распределенной случайной величины постоянна на отрезке и равна нулю вне этого отрезка.

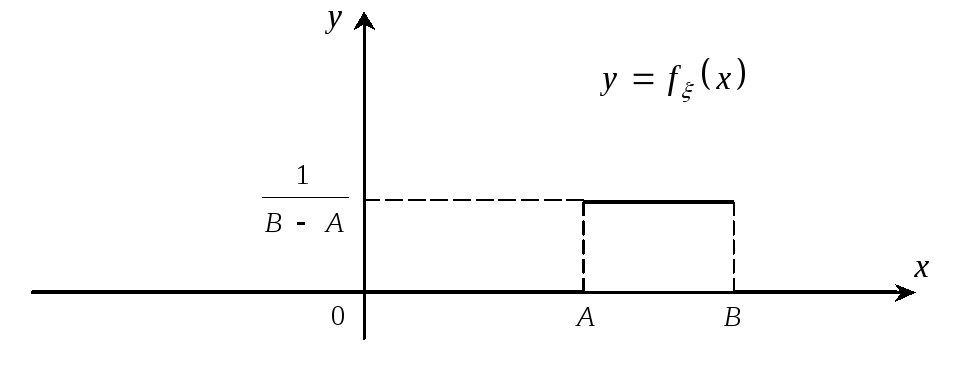
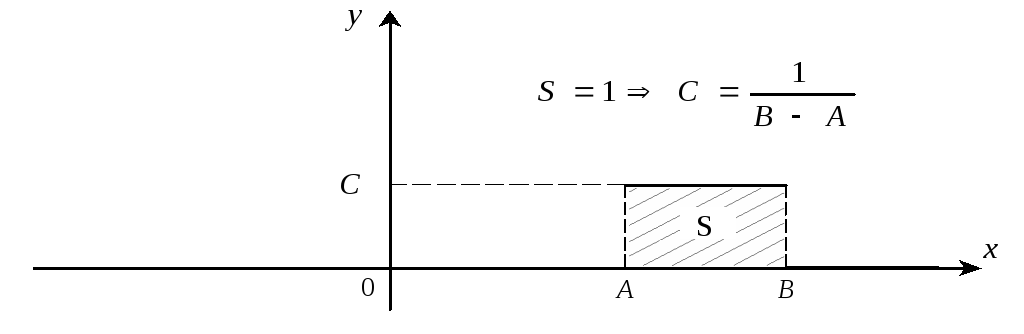
Подграфиком плотности распределения является прямоугольник. Поэтому площадь полученного прямоугольника равна единице.

Найдем функцию распределения.

Если , то площадь подграфика плотности распределения равна нулю. Тогдапри.

Рассмотрим .

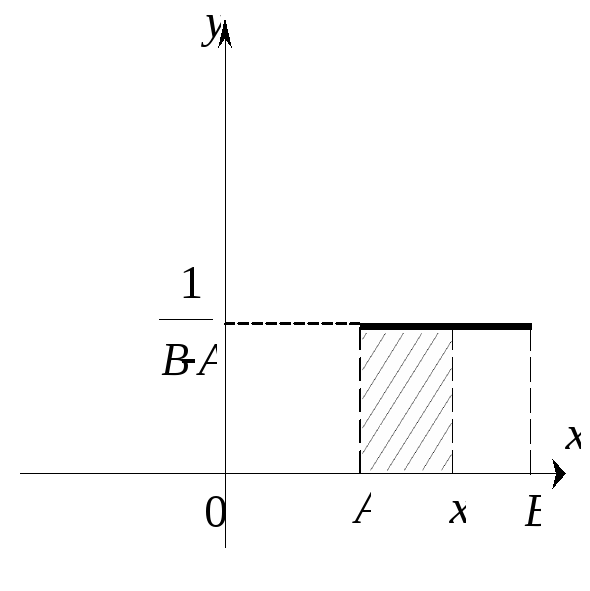
Тогда .

Очевидно, что при имеем.

Запишем функцию распределения равномерно распределенной на отрезке случайной величины:

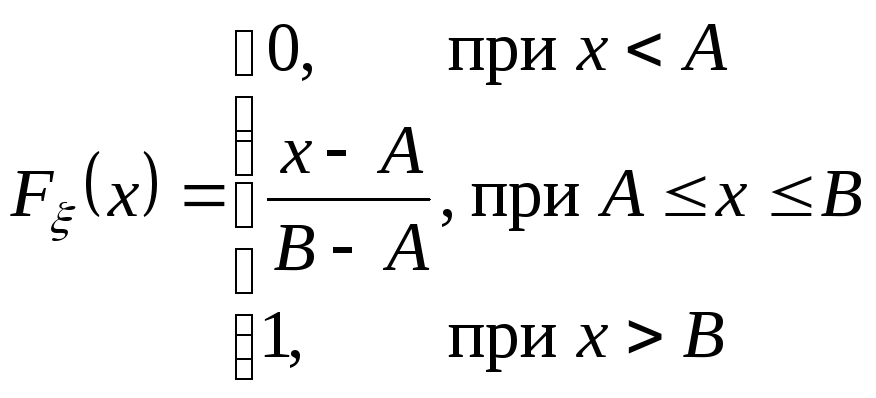
График этой функции:

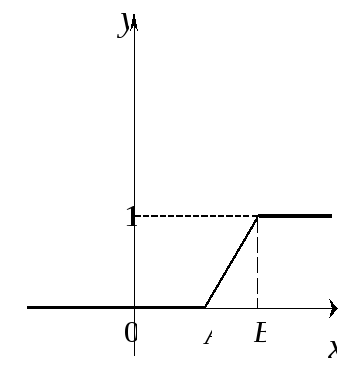
Пусть , тогда

.

Итак, если отрезок полностью лежит на отрезке, то вероятность попадания в отрезокравномерно распределенной случайной величины пропорциональна его длине.

Найдем основные характеристики случайной величины , равномерно распределенной на отрезке.

1. 

.

2. 

Найдем начальный момент второго порядка случайной величины

.

Тогда

.

3. 

Из определения медианы . Тогдаи. Итак,.

Плотность распределения равномерно распределенной величины постоянна на отрезке . Поэтому мода равномерно распределенной величины интереса не представляет.

Пример 1. Задан график плотности распределения случайной величины.

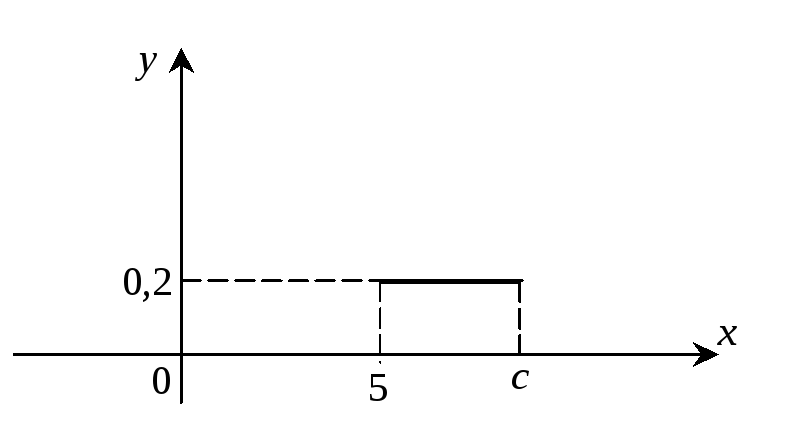
Найти константу с,и.

Плотность распределения постоянна на отрезке и вне его равна нулю. Поэтому случайная величинаравномерно распределена на отрезке. Подграфик плотности распределения равен единице. Тогдаи. Определены параметры равномерно распределенной случайной величины. Тогда

;

;

.

Пример 2. Случайная величинаравномерно распределена, причеми. Записать функцию распределения случайной величины.

Пусть интервал, на котором случайная величинараспределена равномерно. Тогда

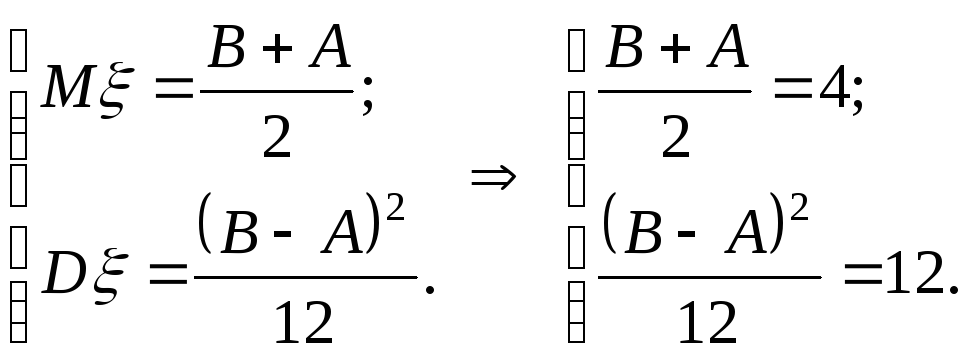
Из условия имеем

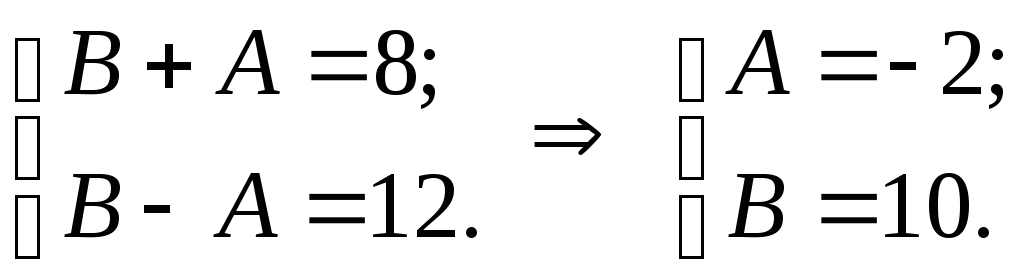
Итак, случайная величина распределена равномерно на отрезке, запишем ее функцию распределения

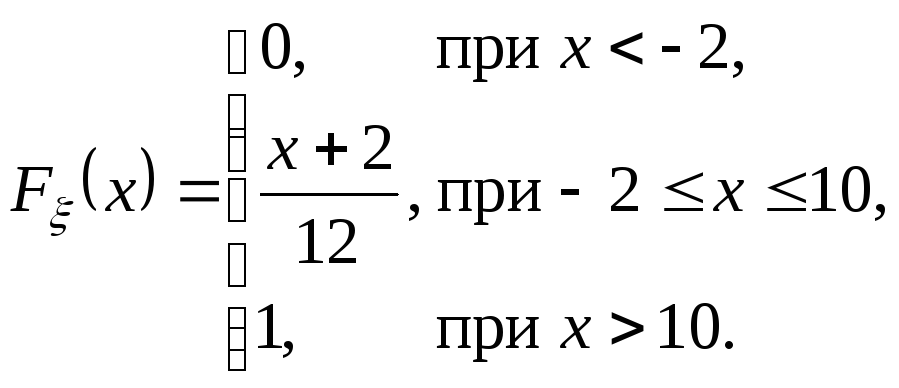
Пример 3. Задан график функции распределения случайной величины

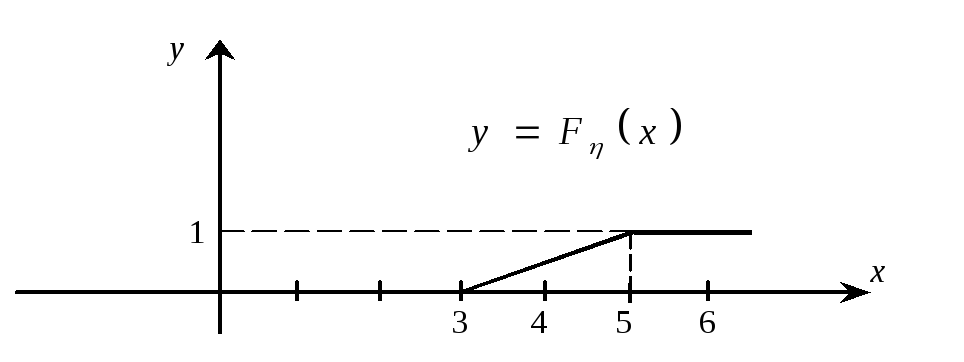
Найти и.

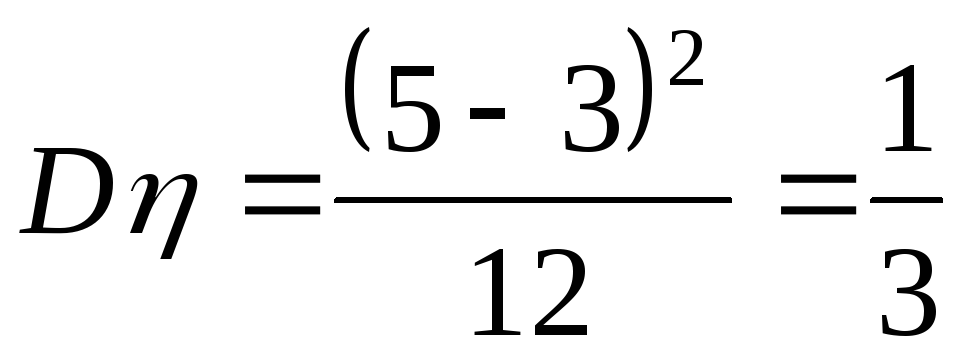По виду графика функции распределения мы заключаем, что случайная величина равномерно распределена на отрезке. Тогдаи.