Задача 6. Найти интегралы методом неопределенных коэффициентов:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. .

Задание для самостоятельной работы

Найти интегралы:

Задача 7. .

Задача 8. .

Задача 9. .

Задача 10. .

Указание. Подынтегральную функцию представить в виде суммы многочлена и правильной дроби (см. задачу 2). Правильную дробь разложить на множители, используя метод неопределенных коэффициентов, проинтегрировать.

Задача 11. Найти интеграл: .

Указание. а) знаменатель разложить на множители (разность кубов);

б) используя метод неопределенных коэффициентов, получить два интеграла 1 и 3 типов;

в) проинтегрировать по алгоритму.

Задача 12. Найти интеграл: .

Найти интегралы, используя метод неопределенных коэффициентов:

Задача 13. .

Задача 14. .

Задача 15. .

Занятие №7. Интегрирование выражений, содержащих тригонометрические функции

Цель занятия: усвоить новые учебные элементы на уровне знаний и умений применять на практике при решении типовой задачи.

Учебные вопросы

1. Интегрирование выражений вида:

.

2. Интегрирование выражений вида:

.

Ход занятия

Краткая информация о новых учебных элементах

1) .

Показатель степени косинуса нечетное положительное число. В этом случае подынтегральное выражение преобразовываем так: извыделяем первую степень косинуса и получаем:

,

т.к. , то, заменив, получим

Применив подстановку, получим интеграл:

,

и решение сведется к интегрированию суммы степенных функций.

2) .

В этом случае показатель степени синуса нечетное положительное число.

Из выделяем первую степень синуса и получаем:

.

Интеграл запишется так:

,

и вопрос опять-таки сведется к интегрированию суммы степенных функций.

3) целое,.

При нахождении данных интегралов применяются формулы понижения степени, которые позволяют привести рассматриваемые интегралы к табличным:

; (1)

. (2)

4) гдедействительные числа.

Для нахождения данных интегралов, подынтегральные функции заменяем, используя формулы произведений тригонометрических функций:

; (3)

; (4)

. (5)

Задача 1. Вычислить интегралы:

1. ;

2. ;

3. .

Решение. 1) .

Представим .

.

2) .

В подынтегральной функции выделим первую степень косинуса, тогда:

.

3) .

Применим формулу понижения степени :

.

Задача 2. Найти интегралы:

1. ;

2. ;

3. .

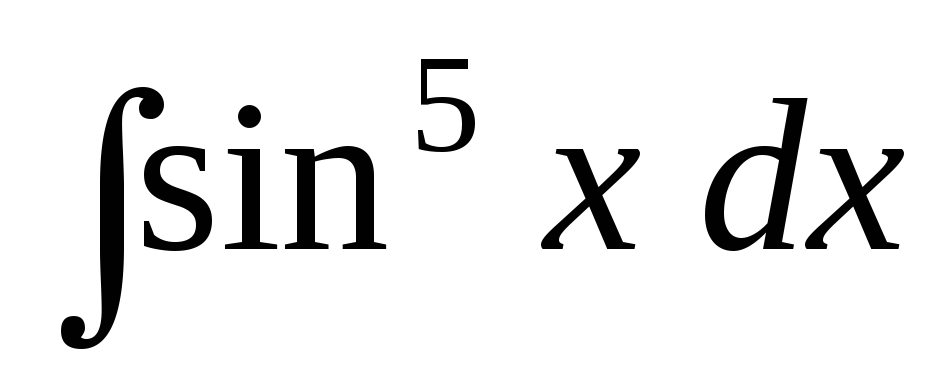Задача 3. Найти интегралы:

1. ;

2. .

Решение. Эти примеры решаются так же, как и примеры 1), 2) задачи 1. У функции, которая под интегралом находится в нечетной степени, выделяем первую степень и применяем указанный выше прием.

1) .

;

.

2) .

;

.

Задача 4. Найти интегралы:

1. ;

2. ;

3. .

Задача 5. Найти интегралы:

а) ,б) .

Решение. а) .

Используем формулу (5):

.

Замечание. , т.к. косинус – функция четная;

, т.к. синус – функция нечетная.

б) .

.

Задача 6. Найти интегралы:

1. ;

2. .

Задание для самостоятельной работы

Задача 7. Найти интегралы:

1. ;

2. ;

3. .

Задача 8. Найти интегралы:

1. ;

2. .

Задача 9. Найти интегралы:

1. ;

2. ;

3. .

63