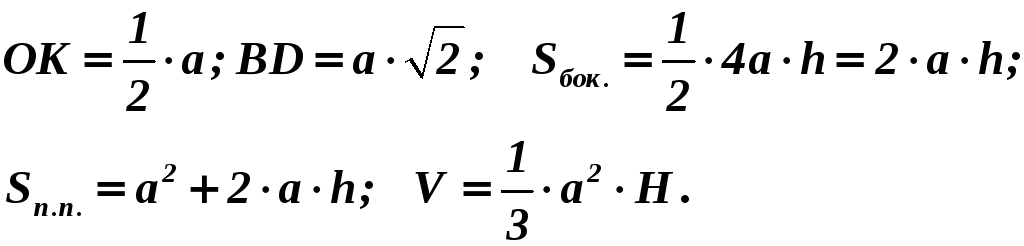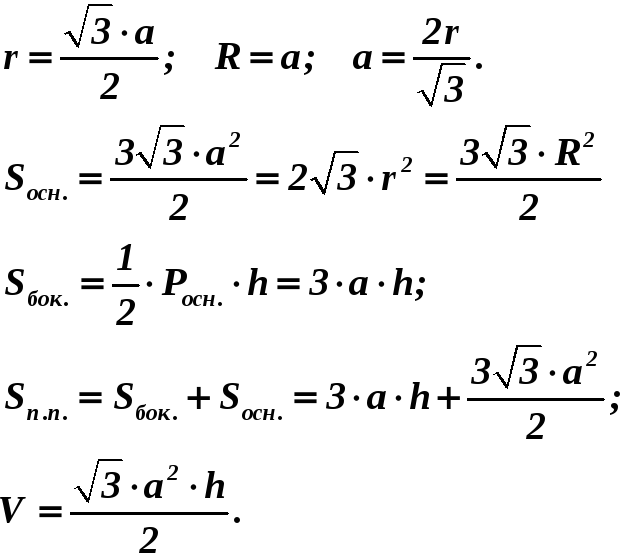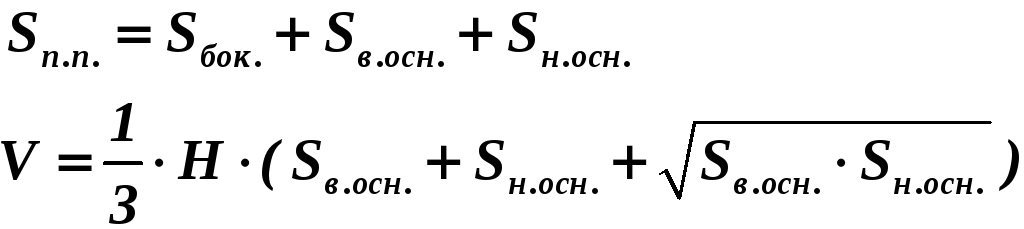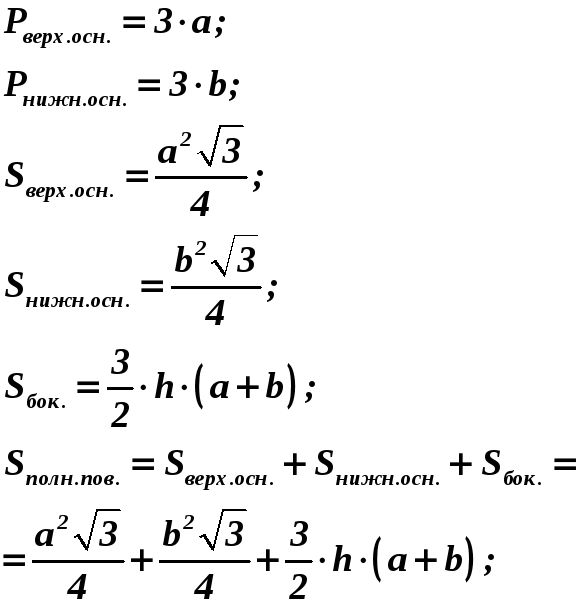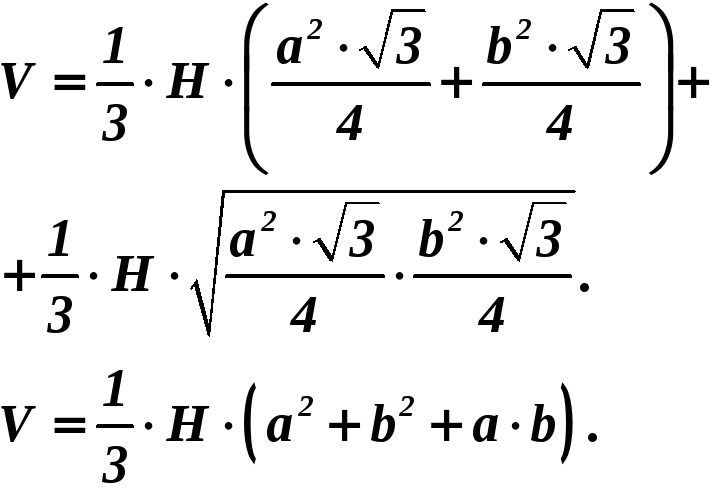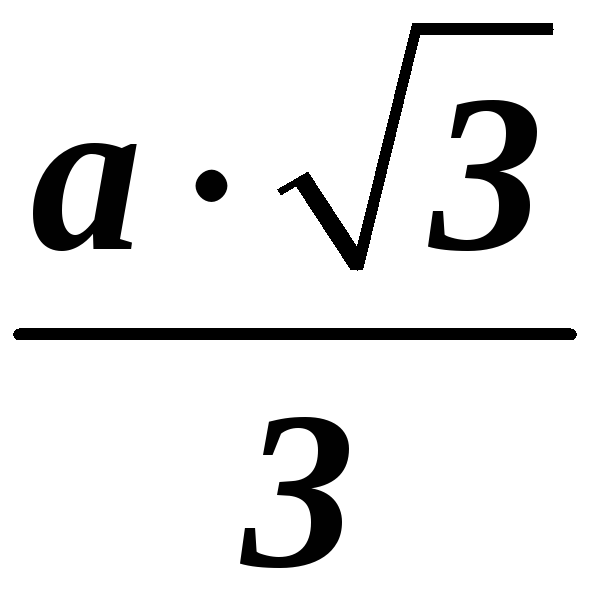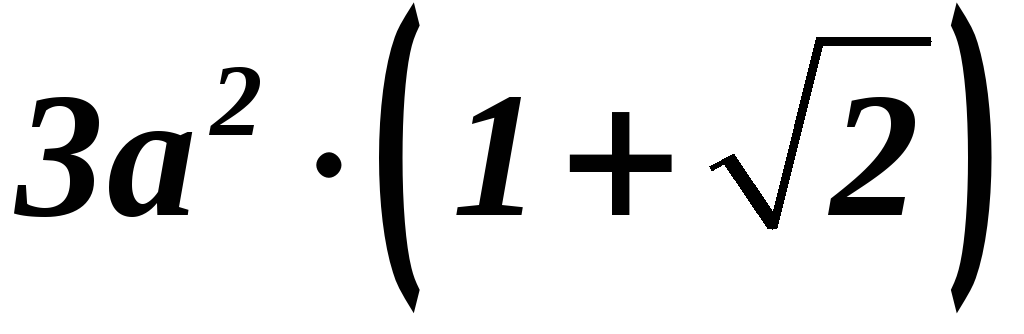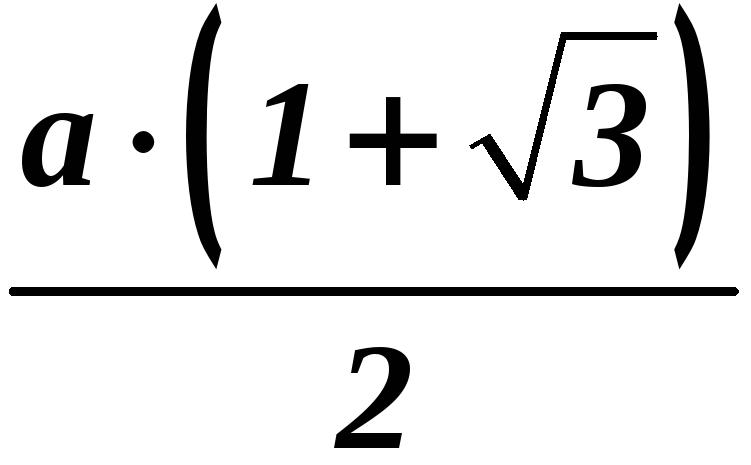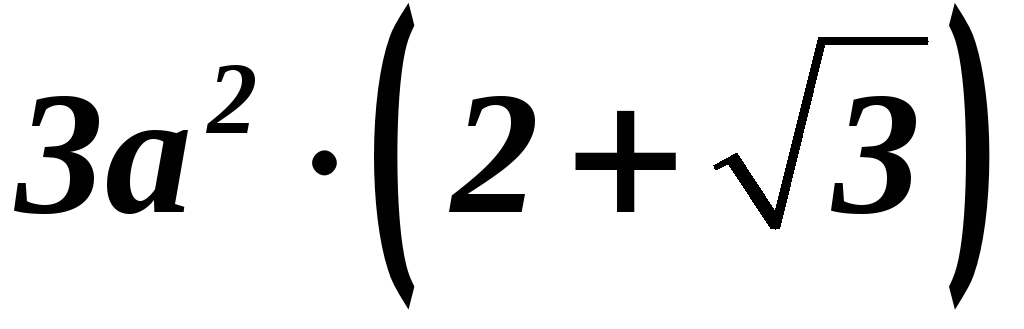Демо вариант
.docДемонстрационный вариант
Часть А
А.1. Заполните пропуски, чтобы получилось истинное утверждение:
Большим кругом называется сечение…
А.2. Сделайте рисунок пирамиды, в основании которой лежит квадрат и одно из боковых рёбер перпендикулярно основанию, обозначьте её: вершину, апофему, высоту, боковые рёбра, основания, боковые грани.
А.3. Запишите, как относятся объёмы двух усечённых пирамид с одинаковыми высотами.
А.4.
Основание призмы
![]() трапеция.
Какие из следующих пар прямых являются
скрещивающимися?
трапеция.
Какие из следующих пар прямых являются
скрещивающимися?
 Варианты
ответов.
Варианты
ответов.
Записать определение скрещивающихся прямых и сделать перебор представленных ответов.
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
А .5.
Укажите плоскость, параллельную прямой,
проходящей через точки пересечения
диагоналей двух граней
.5.
Укажите плоскость, параллельную прямой,
проходящей через точки пересечения
диагоналей двух граней
![]() и
и
![]() параллелепипеда
параллелепипеда
![]() .
.
Варианты ответов.
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
А.6.
Основание пирамиды
![]() параллелограмм.
Укажите плоскость, параллельную
плоскости, проходящей через середины
рёбер
параллелограмм.
Укажите плоскость, параллельную
плоскости, проходящей через середины
рёбер
![]() .
.
Варианты
ответов. 1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
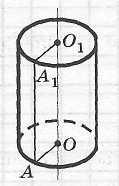
А.7.
Расстояние между осью цилиндра и
параллельным ему сечением равно
![]() .
Радиус основания и высота цилиндра
равны
.
Радиус основания и высота цилиндра
равны
![]() .
Найдите площадь сечения.
.
Найдите площадь сечения.
Решение.
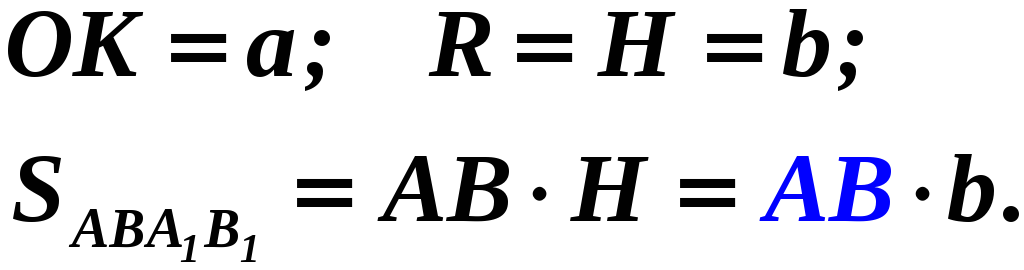

Рассмотрим
![]() равнобедренный,
равнобедренный,![]() .
.
![]() (так как треугольник
равнобедренный),
(так как треугольник
равнобедренный),
![]() .
По теореме Пифагора получим
.
По теореме Пифагора получим
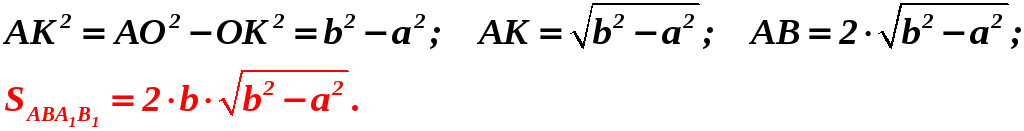
А.8.
Боковое ребро правильной треугольной
пирамиды равно
![]() ,
а сторона основания
,
а сторона основания
![]() .
Найдите тангенс угла наклона боковой
грани к плоскости основания.
.
Найдите тангенс угла наклона боковой
грани к плоскости основания.
Решение.
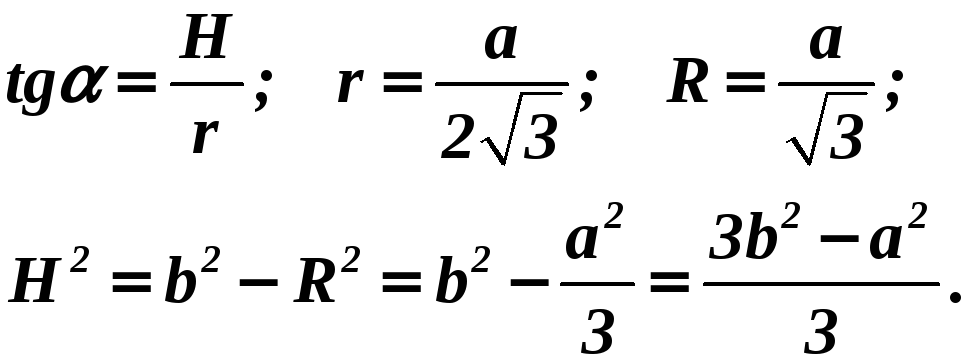
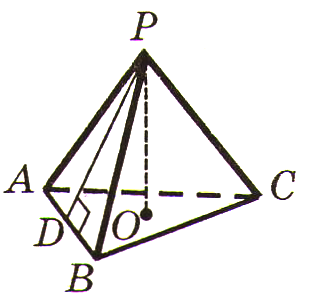
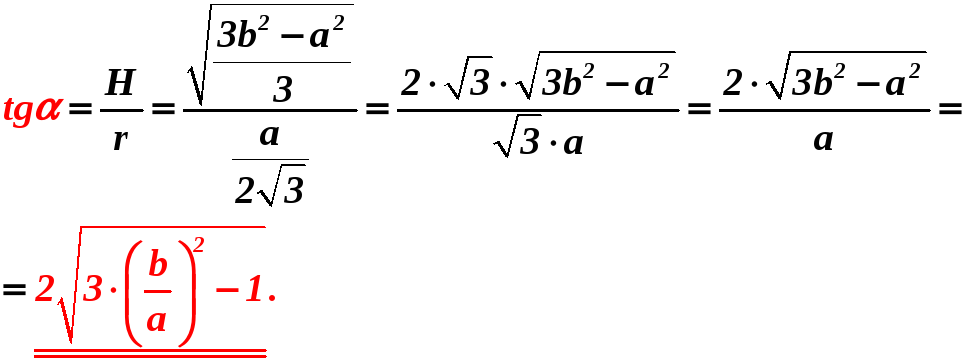 А.9.
Через вершину
А.9.
Через вершину
![]() квадрата
квадрата
![]() проведён перпендикуляр
проведён перпендикуляр
![]() к плоскости квадрата. Найдите расстояние
от точки
к плоскости квадрата. Найдите расстояние
от точки
![]() до прямой, проходящей через середины
сторон
до прямой, проходящей через середины
сторон
![]() ,
если
,
если
![]() .
.
Р H


В A M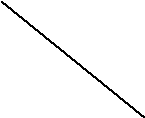



K N
D C
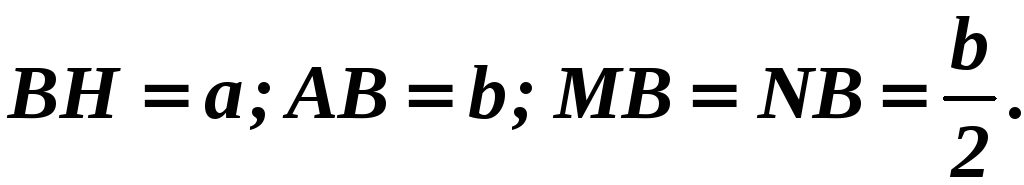
![]() равнобедренный
треугольник. Отрезок
равнобедренный
треугольник. Отрезок
![]() диагональ
квадрата
диагональ
квадрата
![]() и равен:
и равен:![]() .
.
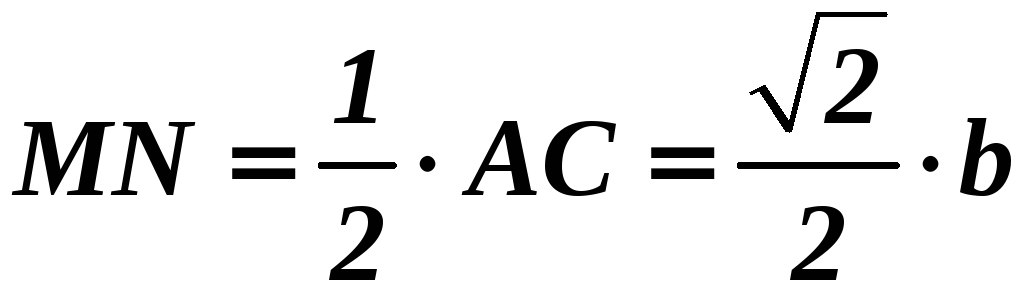 ,
как средняя линия
,
как средняя линия
![]() .
.
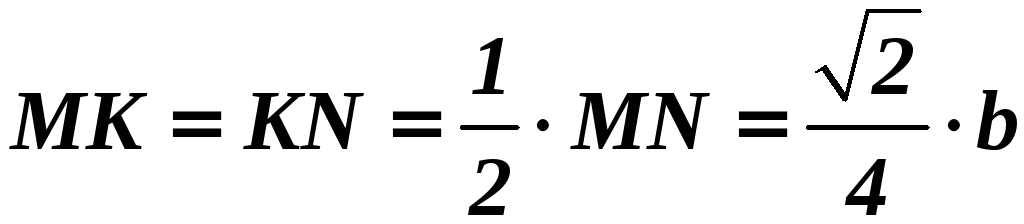 .
.
Рассмотрим
треугольник
![]() (по теореме Пифагора):
(по теореме Пифагора):
 .
.
Рассмотрим
треугольник
![]() (по теореме Пифагора):
(по теореме Пифагора):
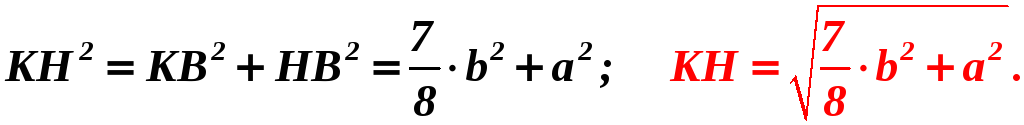
А.10. В основании наклонной призмы лежит правильный треугольник.
Радиус
окружности, вписанной в основание, равен
![]() ,
а её боковое ребро, равное
,
а её боковое ребро, равное
![]() ,
наклонено к плоскости основания под
углом
,
наклонено к плоскости основания под
углом
![]() .
Найдите объём призмы.
.
Найдите объём призмы.
![]()
 равносторонний
треугольник,
равносторонний
треугольник,

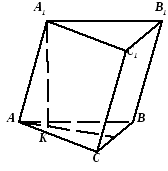
А.11.
Высота правильной четырёхугольной
призмы
![]()
р авна
авна
![]() ,
а сторона основания
,
а сторона основания![]() .
Найдите расстояние между вершиной
.
Найдите расстояние между вершиной
![]() и точкой пересечения диагоналей грани
и точкой пересечения диагоналей грани
![]() .
.
Решение.
![]()
Найдём диагональ
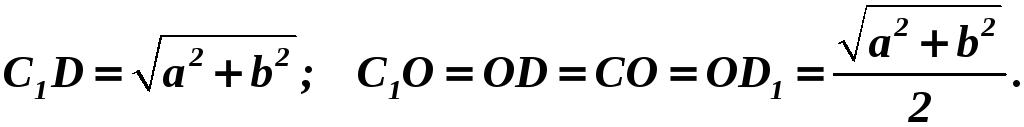
Найдём высоту
равнобедренного треугольника
![]() :
:
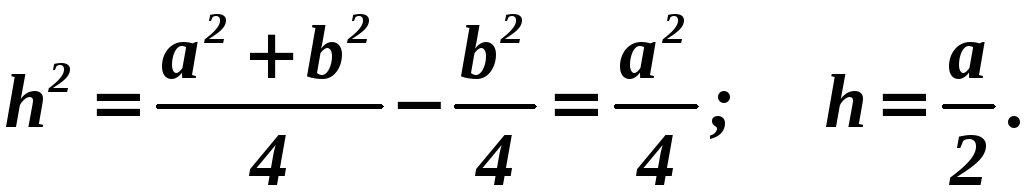
Высота, опущенная
из точки
![]() на сторону
на сторону
![]() ,
делит
,
делит
![]() на два равных отрезка. Найдём проекцию
на два равных отрезка. Найдём проекцию
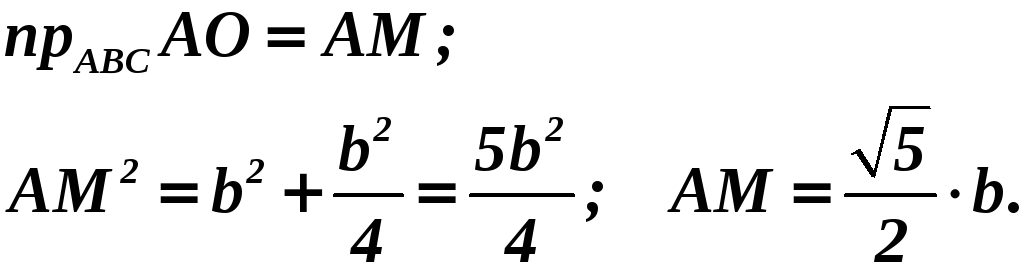
Найдём искомое
расстояние
![]() .
.

А.12.
Н айдите
объём конуса, если угол при вершине его
осевого сечения равен
айдите
объём конуса, если угол при вершине его
осевого сечения равен
![]() ,
а радиус описанного около конуса шара
равен
,
а радиус описанного около конуса шара
равен
![]() .
.
Решение.

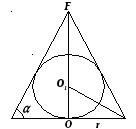
Замечания.
1. Шар можно вписать в любой конус.
2. Шар касается основания конуса в его центре и боковой поверхности конуса по окружности, лежащей в плоскости, параллельной основанию конуса.
3. Центр шара лежит на оси конуса и совпадает с центром окружности, вписанной в треугольник, являющийся осевым сечением конуса.
Рассмотрим
осевое сечение конуса. Обозначим сторону
треугольника![]() .
Треугольник будет равносторонним, так
как угол при вершине равен
.
Треугольник будет равносторонним, так
как угол при вершине равен
![]() ,
образующие конуса являются сторонами
треугольника (осевого сечения), то есть
тоже
,
образующие конуса являются сторонами
треугольника (осевого сечения), то есть
тоже
![]() .
.
Радиус описанной около равностороннего треугольника окружности и высота конуса:
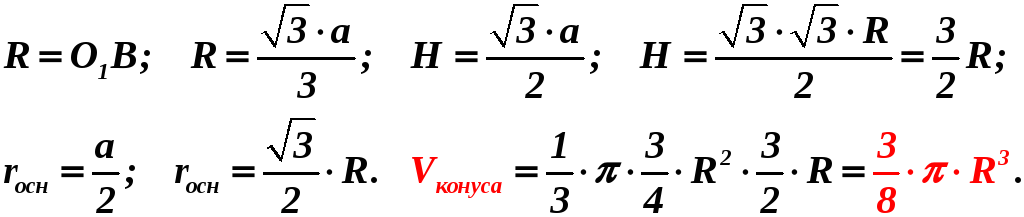
А.13.
Объём цилиндра равен
![]() ,
а радиус его основания
,
а радиус его основания
![]() .
Найдите площадь полной поверхности
цилиндра.
.
Найдите площадь полной поверхности
цилиндра.
Решение.
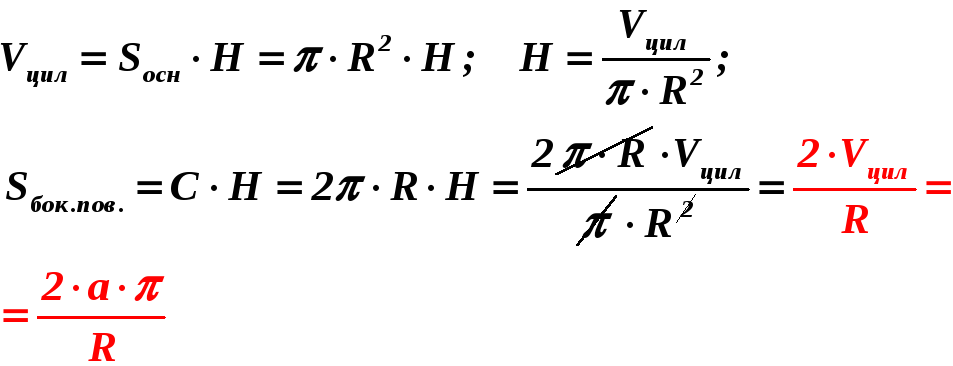
А14.
Основание прямой призмы – прямоугольник
со сторонами
![]() ,
а её высота равна
,
а её высота равна
![]() .
Найдите тангенс угла между диагональю
призмы и плоскостью большей по площади
боковой грани.
.
Найдите тангенс угла между диагональю
призмы и плоскостью большей по площади
боковой грани.
Решение.
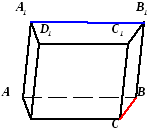
С1
B1
А1
B
D1
А
С1
D
c
a
b


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


По теореме косинусов, получим:

А15.
Расстояние между плоскостью основания
конуса и параллельной ей секущей
п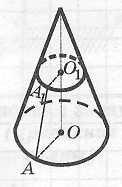 лоскостью
равно
лоскостью
равно
![]() .
Высота конуса равна
.
Высота конуса равна
![]() ,
а радиус сечения
,
а радиус сечения
![]() .
Найдите площадь основания.
.
Найдите площадь основания.
Решение.
Обозначим вершину
конуса через
![]() .
.
![]() .
.
Треугольники
![]()

Часть В
В1.
Основание пирамиды – треугольник со
сторонами
![]() .
Боковые грани наклонены к основанию
под углом
.
Боковые грани наклонены к основанию
под углом
![]() .
Найдите высоту пирамиды.
.
Найдите высоту пирамиды.
Р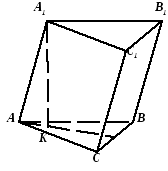 ешение.
ешение.

В2.
Высота правильной шестиугольной призмы
равна
![]() ,
а площадь основания
,
а площадь основания
![]() .
Найдите длину большей диагонали призмы.
.
Найдите длину большей диагонали призмы.
![]()
 п
п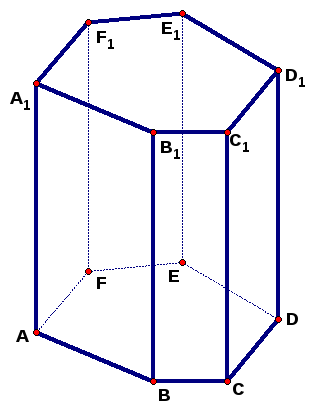

 равильная
шестиугольная призма; в основании
правильный шестиугольник
равильная
шестиугольная призма; в основании
правильный шестиугольник
![]() со стороной
со стороной
![]() .
.
![]() .
Проведём из вершины
.
Проведём из вершины
![]() диагонали
диагонали
![]() и оценим их длины
и оценим их длины
![]()
 .
.
 Угол
Угол
![]() .
По теореме косинусов найдём
.
По теореме косинусов найдём
![]() :
:
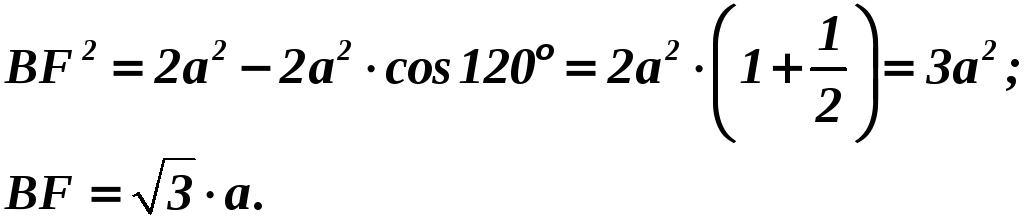
Сравним
![]() .
Значит, большая диагональ
это
.
Значит, большая диагональ
это
![]() так
как проекция наклонной
так
как проекция наклонной
![]() большая.
большая.
Найдём площадь
правильного шестиугольника![]() :
:
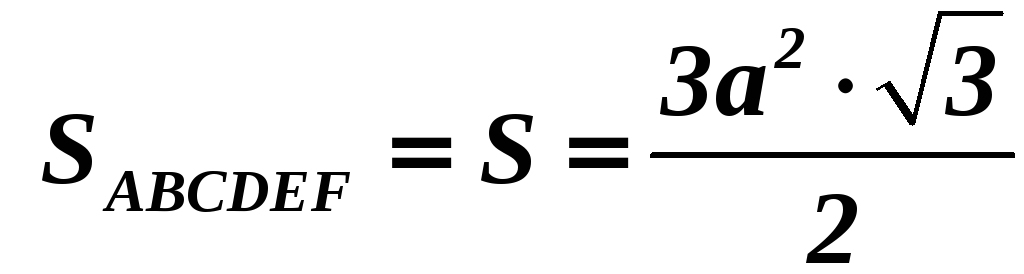 .
Выразим сторону шестиугольника:
.
Выразим сторону шестиугольника:
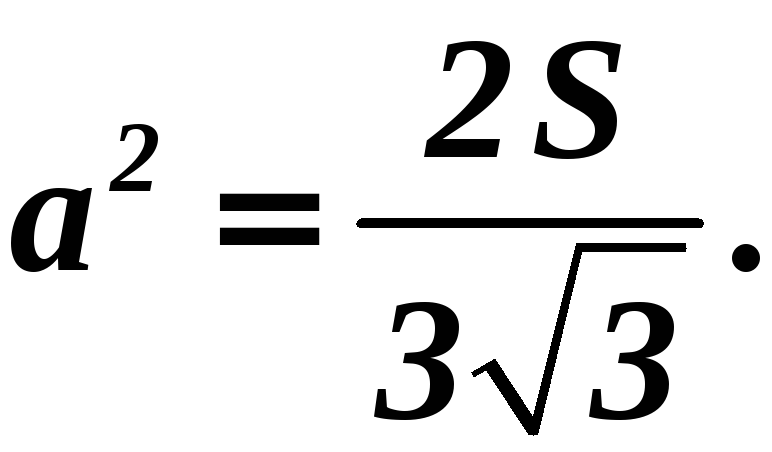
Рассмотрим
треугольник
![]() прямоугольный,
так как призма правильная, по теореме
Пифагора найдём искомую диагональ:
прямоугольный,
так как призма правильная, по теореме
Пифагора найдём искомую диагональ:
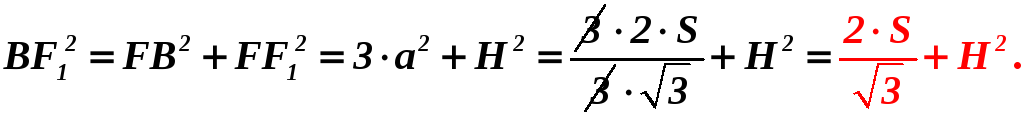



|
Основные формулы стереометрии |
||||||||||
|
Призма
|
Площадью
боковой поверхности призмы
называется
сумма площадей ее боковых граней:
Площадь
боковой поверхности прямой призмы
равна
произведению периметра основания на
высоту призмы:
Объем
прямоугольного параллелепипеда равен
произведению
площади основания на высоту:
Объем
куба равен кубу его ребра:
Объем
прямой призмы, основанием которой
является
прямоугольный треугольник, равен
произведению площади основания на
высоту:
|
|||||||||
|
Пирамида
|
Площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.
Площадь
боковой поверхности правильной
пирамиды равна половине произведения
периметра основания на апофему:
Для
правильной
Площадь
боковой поверхности пирамиды, в которой
все двугранные углы при основании
равны
|
|||||||||
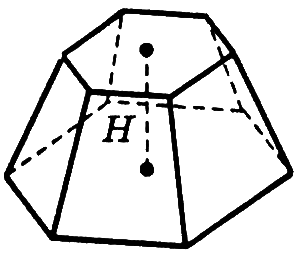
|
Усеченная пирамида
|
Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.
Площадь
боковой поверхности правильной
усеченной пирамиды
равна произведению полусуммы периметров
ее оснований на апофему:
где
|
|||||||||
|
Цилиндр
|
Площадью
боковой поверхности цилиндра
называется
площадь ее развертки:
Площадью
полной поверхности цилиндра
называется сумма площадей боковой
поверхности и двух
оснований:
|
|||||||||
|
Конус
|
Площадь
боковой поверхности конуса вычисляется
по формуле
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания:
|
|||||||||
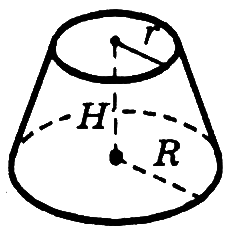
|
Усеченный конус
|
Площадь
боковой поверхности усеченного конуса
вычисляется
по формуле
Площадь
полной поверхности усеченного конуса
с
образующей
|
|||||||||
|
Шар
|
Объем
шара с диаметром
Площадь
сферы радиуса
|
|||||||||
|
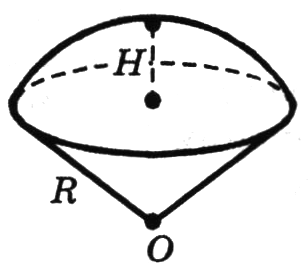
Шаровой сегмент
|
|
|||||||||
|
Шаровой сектор
|
|
|||||||||
|
Шаровой слой
|
|
|||||||||
|
Основные формулы планиметрии, используемые для решения стереометрических задач |
||||||||||
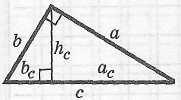
|
Произвольный треугольник
|
Теорема
синусов:
Теорема
косинусов:
Площадь треугольника:
Формулы
радиусов: |
|||||||||
|
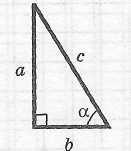
Прямоугольный треугольник
|
Теорема
Пифагора:
Тригонометрические функции:
Формулы
радиусов:
Площадь:
Метрические соотношения:
|
|||||||||
|
Равносторонний треугольник
|
Формула
высоты:
Площадь:
Формулы
радиусов:
|
|||||||||
|
Произвольный параллелограмм
|
Связь между диагоналями и сторонами:
Площадь:
|
|||||||||
|
Прямоугольник
|
Площадь:
Радиус
описанной окружности:
|
|||||||||
|
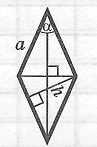
Ромб
диагонали. |
Площадь:
Радиус
вписанной окружности:
|
|||||||||
|
Квадрат
|
Площадь:
Формулы
радиусов:
|
|||||||||
|
Трапеция |
Площадь:
|
|||||||||
|
Правильная пирамида |
||||||||||
|
S
A D C E H O B K a F h |
|
|||||||||
|
Правильная треугольная пирамида |
||||||||||
|
A |
H – высота, h – апофема а – сторона основания AB = BC = AC = a (в основании – правильный треугольник)
|
|||||||||
|
|
||||||||||
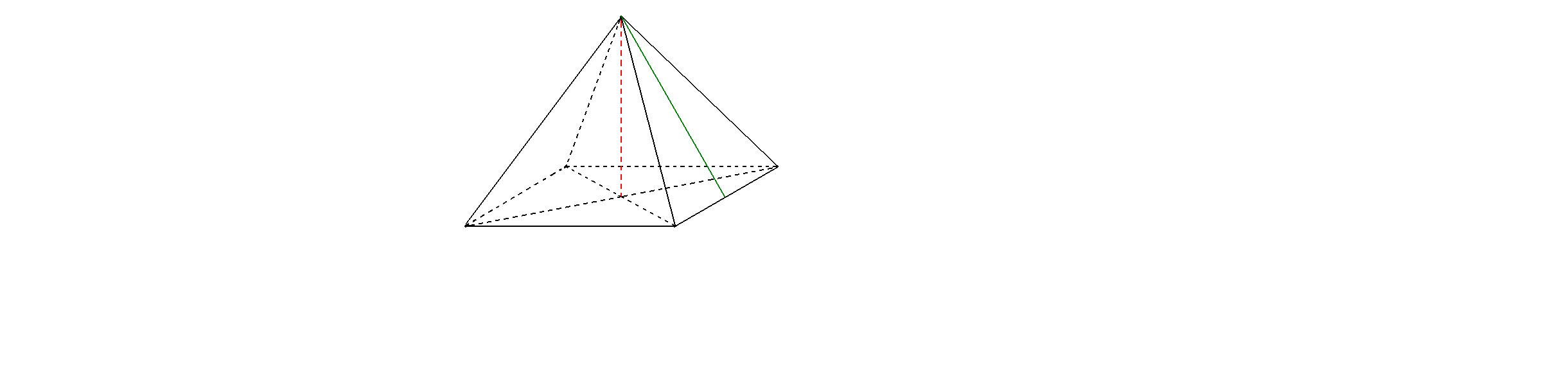
|
Правильная четырехугольная пирамида |
||||||||||
|
Р
С А В D O H a h K |
|
|||||||||
|
H – высота, h – апофема; а – сторона основания AB = BC = CD = DA = a (в основании – квадрат); К – середина DC.
|
||||||||||
|
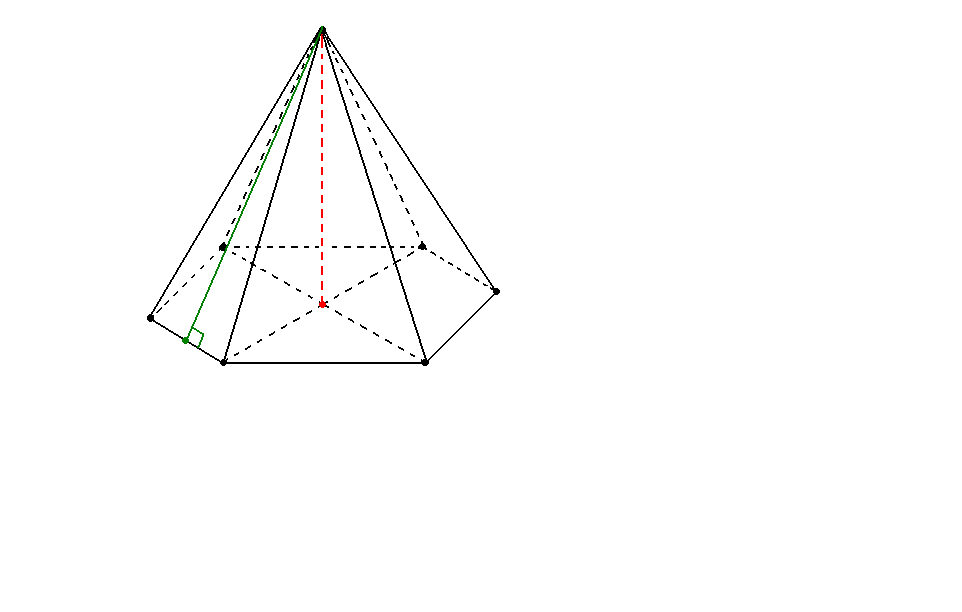
Правильная шестиугольная пирамида |
||||||||||
|
S
А В С D О E K h F a H
|
||||||||||
|
Усеченная пирамида |
||||||||||
|
P P А А А А O OO1= H – высота
|
||||||||||
|
Правильная треугольная усеченная пирамида – боковые грани – равные между собой равнобокие трапеции. |
||||||||||
|
Δ ABC и Δ A1B1C1 – равносторонние треугольники. OO1 = H – высота ; КК1 = h – апофема.
А В K С О a M h H b
|
|
|||||||||
|
Правильная четырехугольная усеченная пирамида – боковые грани – равные между собой равнобокие трапеции. |
||||||||||
|
А C B H h K D O b a |
||||||||||
|
ABCD и A1B1C1D1 – квадраты OO1 = H – высота KK1 = h – апофема
|
||||||||||
|
Правильные многоугольники |
||||||||||
|
|
|
|
|
|
Связь м/у
|
|||||
|
3 |
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|||||
|
6 |
|
|
|
|
|
|||||
|
8 |
|
|
|
|
|
|||||
|
12 |
|
|
|
|
|
|||||


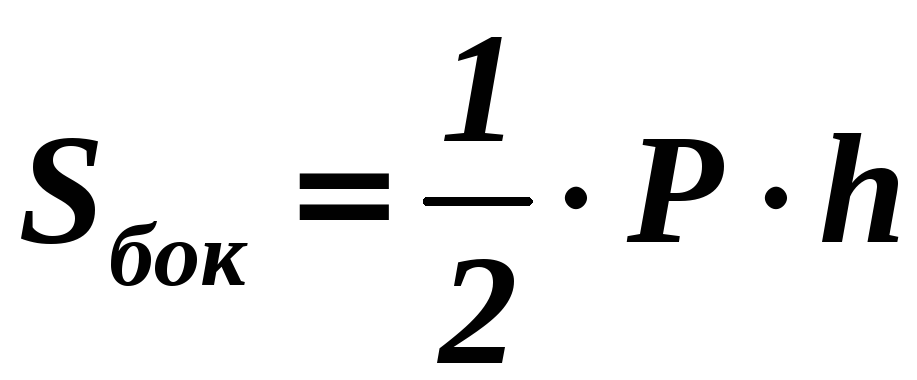 .
.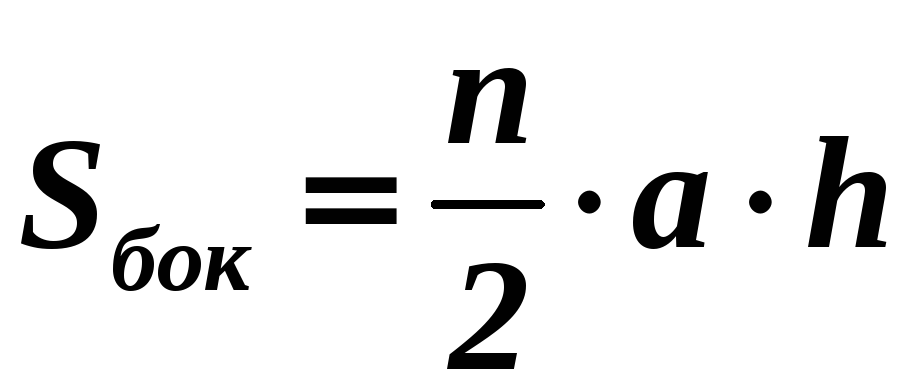 .
.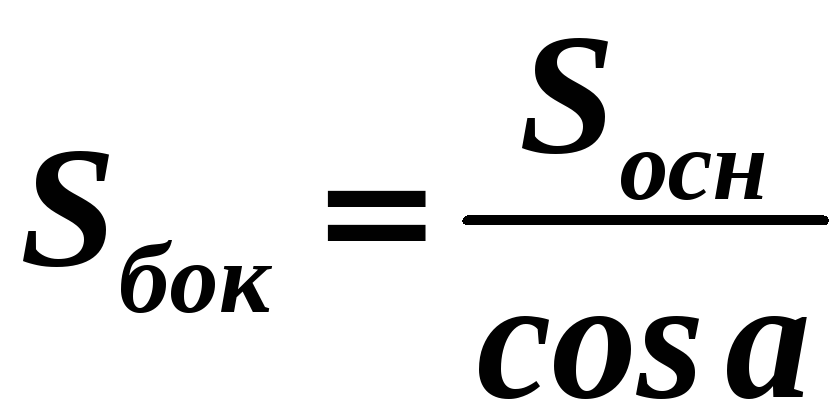 ,
где
,
где

 ,
,
 ,
где
,
где


 .
.
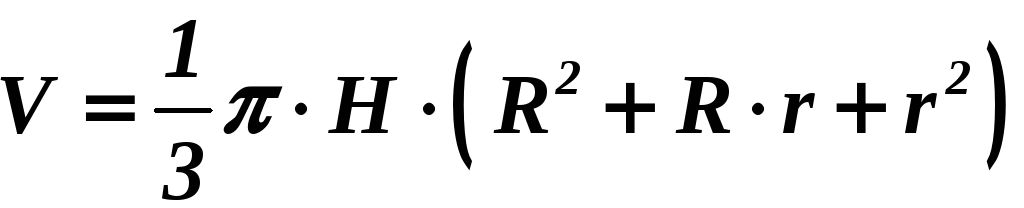

 .
.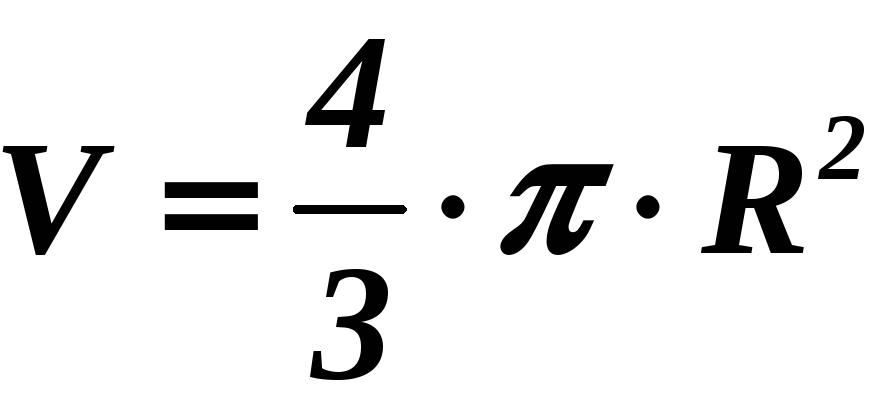

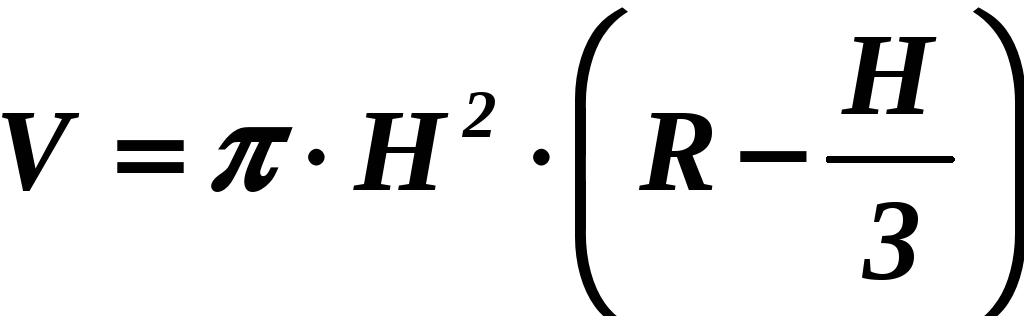


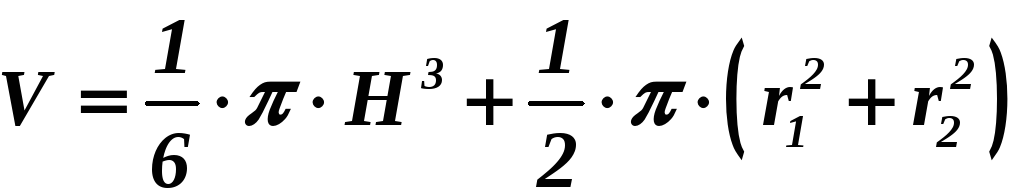

 полупериметр.
полупериметр. .
.
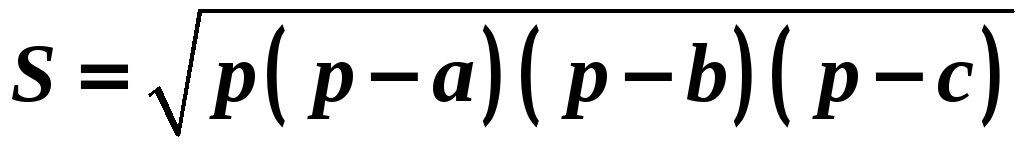 (формула
Герона).
(формула
Герона). .
.
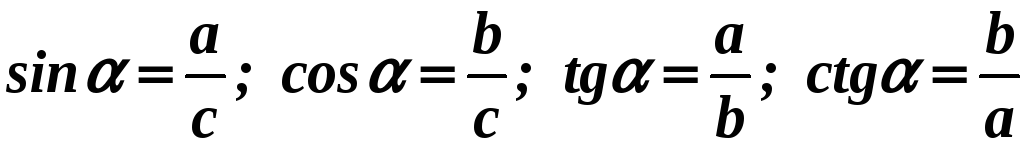 .
. .
. .
.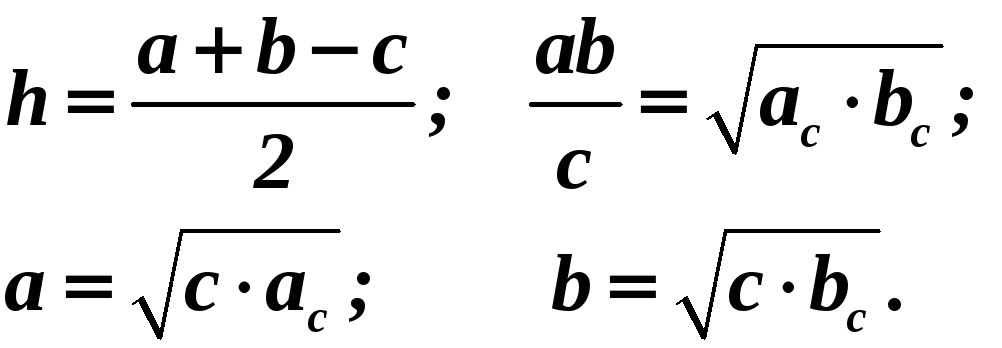 .
.
 .
.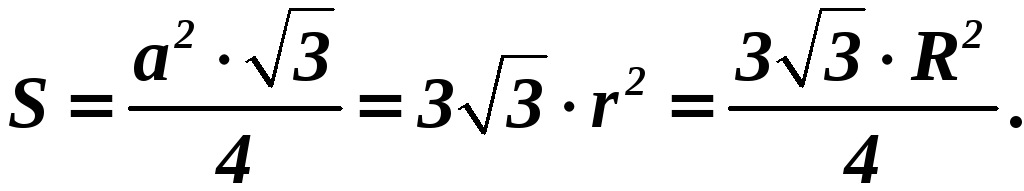

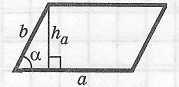
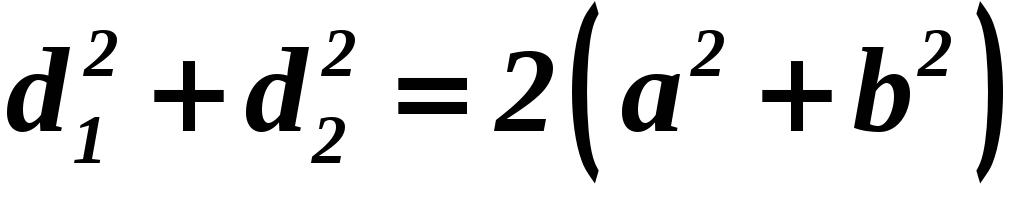 .
.
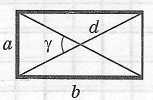
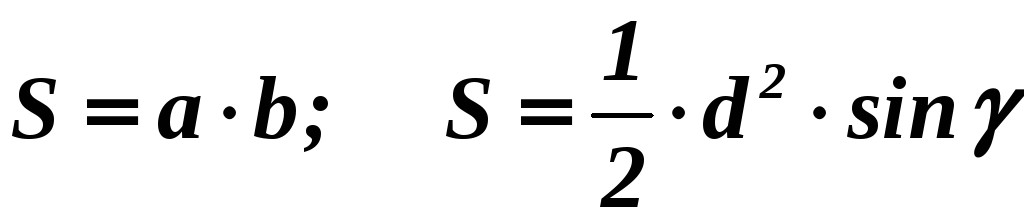 .
.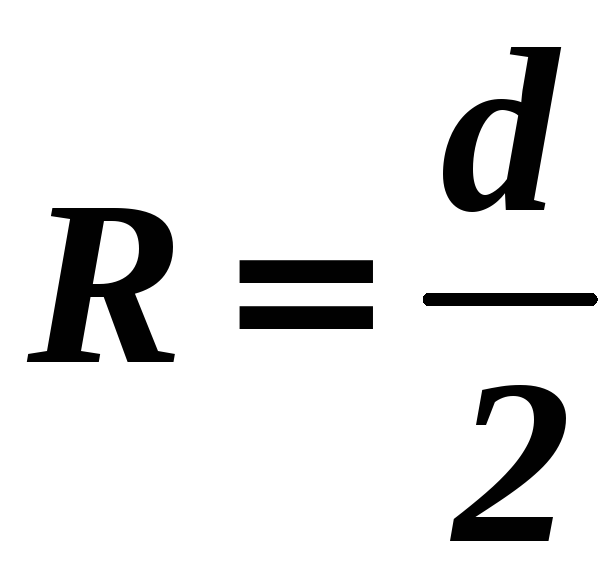
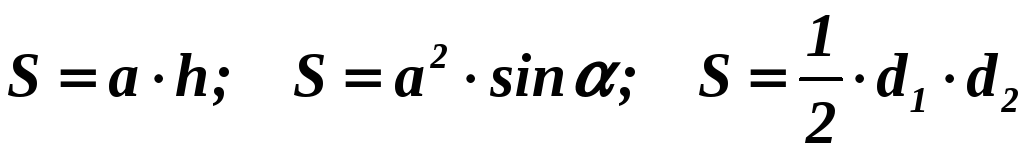 .
.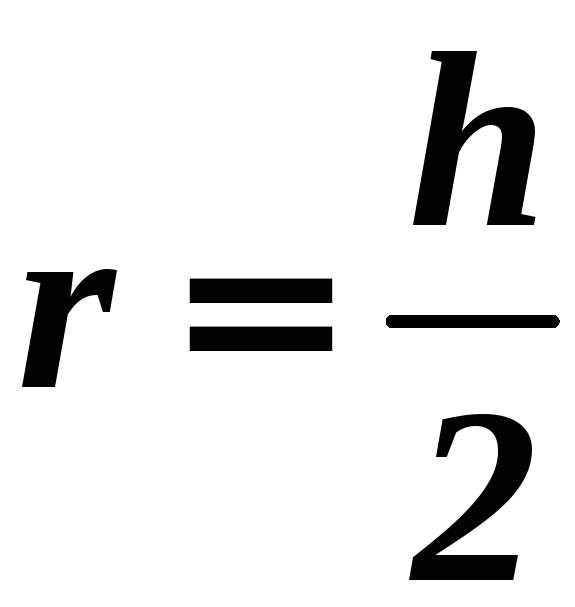 .
.
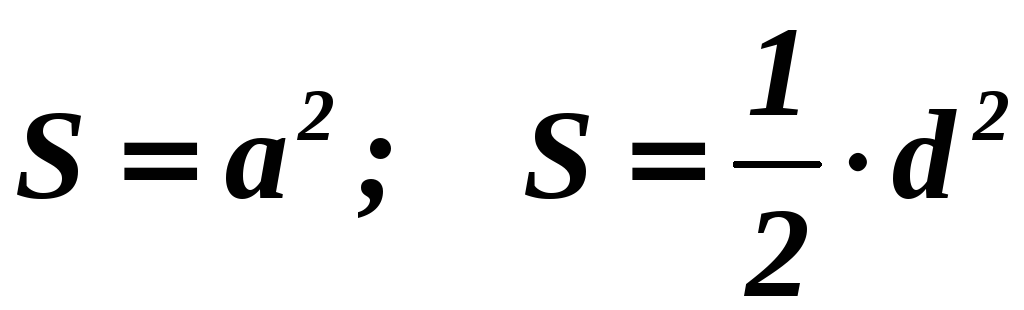 .
.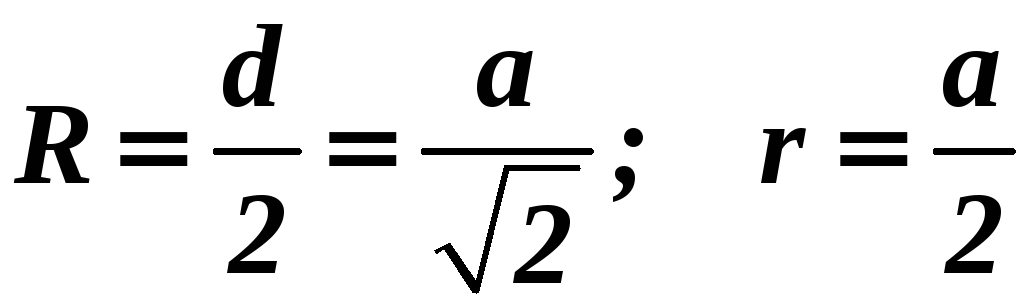 .
.
 .
.