Определение кажущейся молекулярной массы и параметров состояния смеси

В теорию газовых смесей введено понятие о средней (кажущейся) молекулярной массе смеси _см, т.е. о молекулярной массе такого воображаемого однородного газа, который по своим свойствам аналогичен рассматриваемой смеси.

Находится кажущаяся молекулярная масса следующим образом. Из определения киломоля вытекает равенство, справедливое для любого однородного газа:

, (24)

где n - количество вещества компонента, моль.

Для смеси по аналогии можно записать:

. (25)

Отсюда, из равенства:

(26)

следует, что:

, (27)

где ;; …;– мольные доли компонентов смеси,моль.

Поскольку то среднюю молекулярную массу можно выразить:

. (28)

Если известен массовый состав смеси, то кажущуюся молекулярную массу смеси вычисляют по уравнению:

. (29)

Если известен объемный состав смеси (объемная доля компонентов), то плотность смеси газов можно вычислить из соотношений:

. (30)

Если газовая смесь задана массовыми долями, то плотность смеси можно определить из соотношения:

. (31)

Удельный объем смеси представляет величину, обратную плотности смеси:

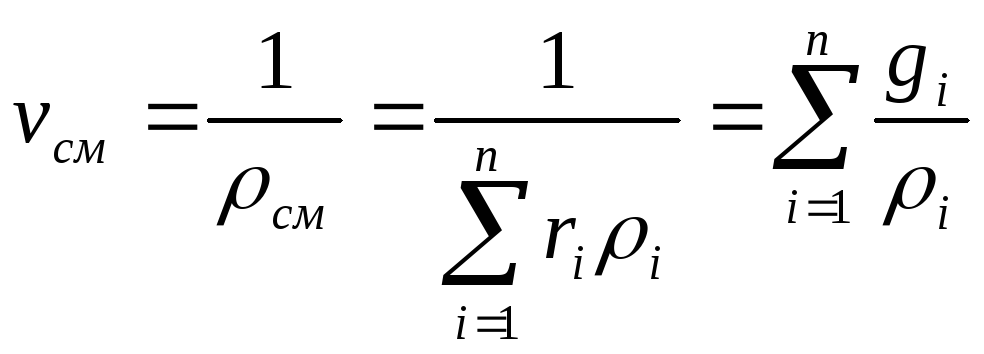. (32)

Объемные доли компонентов смеси удобно использовать для вычисления парциальных давлений ее составных частей. Из уравнения:

, (33)

следует, что:

, (34)

т.е. для любого компонента смеси можно записать:

. (35)

24 Теплоемкость

Теплоемкостью называется количество теплоты, которое необходимо подвести к какой-либо количественной единице рабочего тела, чтобы нагреть ее на 1 градус (1 °С или 1 К).

Истинная теплоемкость – производная количества теплоты по температуре, она определяется в виде отношения:

, (36)

откуда:

. (37).

Теплоемкость зависит от характера процесса, при котором подводится или отводится теплота, поэтому при экспериментальном определении ее значения обычно используют два термодинамических процесса, протекающих при постоянном объеме и давлении. Значения теплоемкостейидля различных веществ сведены в таблицы.

Подведенная при постоянном объеме теплота, когда dl=0, расходуется только на изменение внутренней энергии. При постоянном давлении некоторое количество теплоты идет также на совершение работы, поэтому для изменения температуры рабочего тела на 1 градус при P = const требуется большее количество теплоты, чем при v = const и, следовательно .

В зависимости от способа определения количества рабочего тела (т.е. от количественной единицы измерения рабочего тела, которую необходимо нагреть) теплоемкости делят на:

• удельные массовые: 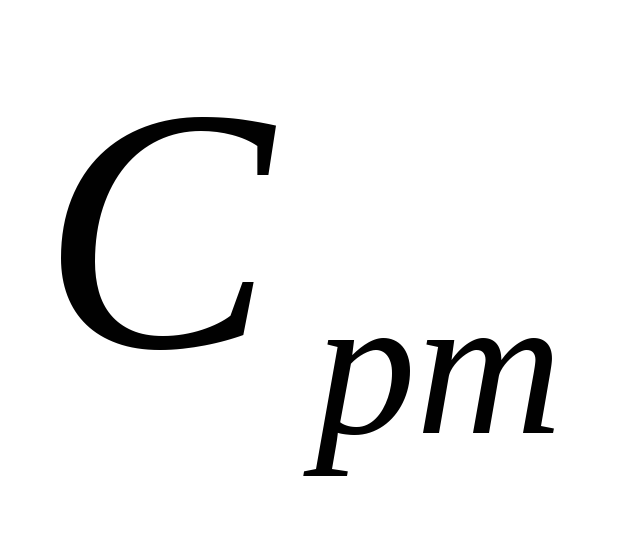и,;

• удельные объемные: и,;

• удельные молярные: 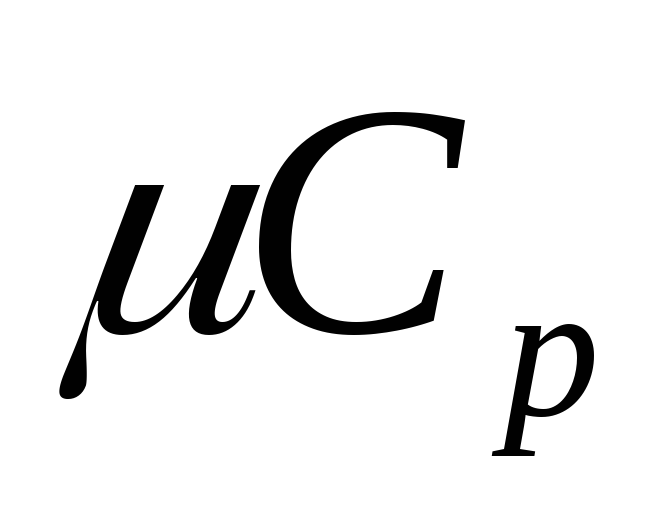и,.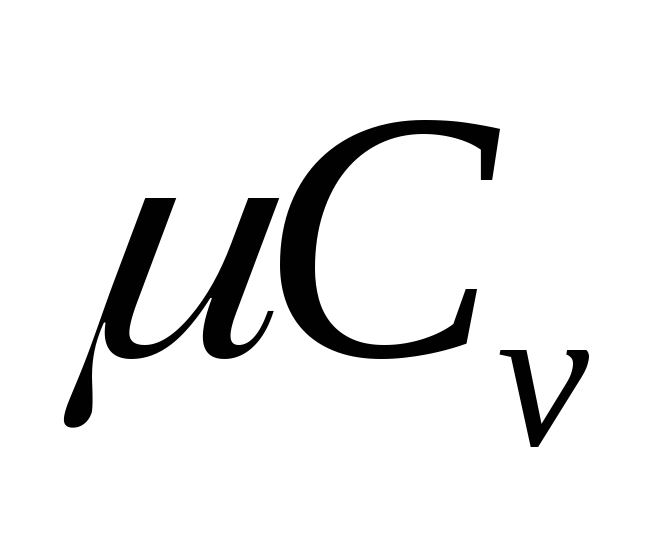

Все они связаны м/у собой соотношениями:

; (38)

; (39)

. (40)

Теплоемкости игаза не зависят ни от объема, ни от давления, и являются однозначными функциями температуры. Иногда, в приближенных расчетах, зависимостью от температуры пренебрегают и значения теплоемкости принимают постоянными. Тогда в соответствии с выражением (37):

. (41)

В большинстве случаев функцию С=f(Т) (см. рисунок 3) приходится учитывать и использовать для определения количества подведенной или отведенной теплоты, которая численно равна площади под характеристикой 1-2 процесса. Количество теплоты можно найти, если использовать средние значения теплоемкости С_ср, при V = const или Р = const определяются отношением:

. (42)

Рисунок 3 – Зависимость теплоемкости от температуры

В этом случае площадь а34в, равна площади а12в. С помощью С_ср, можно рассчитать количество теплоты по формуле аналогичной выражению (42).

Если необходимо получить количество подведенной теплоты в интервале температур T₁ – T₂ , то поступают следующим образом: сначала определяют количество теплоты

,

,

а затем:

. (43)

Для многих теплотехнических расчетов зависимость С=f(Т) принимают линейной, тогда:

. (44)

В этом случае

, (45)

тогда:

. (46)

Если рабочим телом является смесь газов, то ее теплоемкость зависит от состава смеси:

(47)