Соединение фаз приемника треугольником.

При включении начала одной фазы с концом другой с образованием замкнутого контура получают соединение треугольником, при этом три фазы приемника включены между линейными проводами, то есть находятся под линейными напряжениями.

Слайд 19

Фазные напряжения приемника равны соответствующим линейным напряжениям источника питания:

Положительное направление фазных напряжений _ab ,_bcи_caсовпадает с положительным направлением фазных токов.

Линейные токи ,_Bи _Cположительные направления от источника к приемнику.

При соединении треугольником приемника получается замкнутый контур, поэтому:

U_л=U_ф

Линейные токи определяются по фазным токам по первому закону Кирхгофа:

Линейные токи равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом.

независимо от характера нагрузки.

При изменении одной из фаз режим работы других фаз остается неизменным, т.к. линейное напряжение генератора остается постоянным.

Соединение треугольником используется для несимметричной нагрузки.

Слайд 20 Мощность трехфазных цепей.

Мгновенная мощность трехфазного источника электрической энергии:

Среднее за период значение мощности, т.е. мощность генератора, равна сумме активных мощностей отдельных фаз.

Слайд 21

Мощность трехфазной цепи при несимметричной нагрузке.

Трехфазная цепь это совокупность трех однофазных цепей, поэтому активная и реактивная мощности трехфазной цепи равны сумме отдельных фаз.

Активная мощность:

Рассчитываются активные мощности:

Реактивные мощности:

Рассчитываются реактивные мощности:

Модуль полной мощности трехфазной цепи:

Слайд 22

Мощность трехфазной цепи при симметричной нагрузке.

При симметричной нагрузке мощности фаз одинаковы, поэтому:

Слайд 23

Так как за номинальные величины обычно принимают линейные напряжения и токи то мощности удобнее выражать через линейные величины Uл иIл. Используя соотношения между линейными и фазными величинами для различных способов соединения получим формулу мощности:

: ,

тогда

Δ: ,

Вывод: при симметричной нагрузке формулы мощности независимо от схемы соединения приемников одинаковы.

Слайд 24

Нелинейные эклектические цепи

Электрическую цепь называют нелинейной, если она содержит элементы, параметры R,L,Cкоторых зависят от значений или направлений тока или напряжений.

На практике в промышленной электронике электрические цепи состоят в основном из нелинейных элементов, т.е. из элементов, у которых ВАХ не являются прямой линией (значения параметров резко изменяются с изменением тока)

Нелинейные ВАХ имеют все полупроводниковые приборы:

1. Полупроводниковые диоды

2. Стабилитроны

3. Термисторы

4. Транзисторы

5. Тиристоры

6. и т.д.

Слайд 25

Нелинейные элементы характеризуются двумя параметрами: статическим Rст и дифференциальным Rдиф. Сопротивлениями. Эти сопротивления изменяются от точки к точке вольт-амперной характеристики

Понятия статического и динамического (дифференциального) сопротивления:

- отношение напряжения на элементе к току в заданной точке его характеристики, где, mU, mI, mR – масштабы для напряжения, тока и сопротивления соответственно. Таким образом, статическое сопротивление нелинейного элемента в любой точке характеристики пропорционально тангенсу угла наклона линии, проведенной из начала координат через эту точку, к оси тока.

- отношение изменения напряжения к изменению тока в заданной рабочей области нелинейного элемента. Таким образом, дифференциальное сопротивление нелинейного элемента в любой точке характеристики пропорционально тангенсу угла наклона касательной линии, проведенной через эту точку, к оси тока.

На графике показаны углы α и β характеризующие значения статического и дифференциального сопротивления нелинейного элемента.

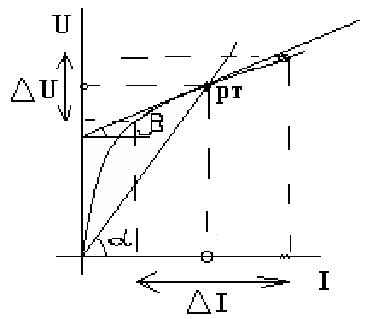
Слайд 26

Анализ и расчет нелинейных цепей осуществляется двумя способами аналитическим или графическим. Электрическое состояние нелинейной цепи, так же как и линейной описывается системой алгебраических уравнений составленных по первому и второму законам Кирхгофа. Однако при этом используется система нелинейных алгебраических уравнений. Общих аналитических методов решения нелинейных уравнений не существует, поэтому решение таких задач осуществляется численными методами. Поэтому в расчете простых нелинейных цепей удобнее применять графические методы. Одним из этих методов является метод пересечения характеристик - это решение нелинейного уравнения определяющего электрическое состояние графическим способом.

Рассмотри участок цепи с последовательно соединенными линейным и нелинейным элементами.

Анализ и расчет нелинейных цепей проводится с помощью метода пересечения характеристик, с использованием метода эквивалентного, активного двухполюсника.

Составим уравнение электрического состояния для цепи:

Холостой ход:

Короткое замыкание:

Слайд 27

Согласно уравнению строится «опрокинутая» ВАХ резистора R.

Правило: если нелинейный элемент соединен последовательно с резистором, то строится «опрокинутая» ВАХ, если параллельно, то строится обычная ВАХ резистора.

Как известно, любая прямая строится по двум точкам, которые соответствуют двум режимам двухполюсника с параметрами EиR.

Пересечение вольт-амперных характеристик нелинейного элемента и резистора дают графическое решение задачи, как показано на графике.

Напряжение и ток на нелинейном элементе находятся методом пересечения характеристик, зная эти параметры можно определить токи и напряжения остальных ветвей цепи.