
- •Завдання для самостійної роботи.
- •Завдання з теми «Лінійна та векторна алгебри. Елементи аналітичної геометрії».
- •Завдання з теми «Диференціальне числення функції однієї змінної».
- •Завдання з теми «Невизначений та визначений інтеграли».
- •Завдання з теми «Диференціальні рівняння та системи».
- •Завдання з теми «Ряди».
- •Зразки виконання завдань.
- •Розв’язання завдань з теми «Лінійна та векторна алгебри. Елементи аналітичної геометрії».
- •Розв’язання завдань з теми «Диференціальне числення функції однієї змінної».
- •Розв’язання завдань з теми «Невизначений та визначений інтеграли».
- •Розв’язання завдань з теми «Диференціальні рівняння та системи».
- •Розв’язання завдань з теми «Ряди».
- •Література
Зразки виконання завдань.
Розв’язання завдань з теми «Лінійна та векторна алгебри. Елементи аналітичної геометрії».
Завдання 1.
Задано
матриці
 і
і
 .
.
Обчислити матриці
 ,
, ,
, ,
, .
.Записати матричне рівняння
 ,
де
,
де ,
у вигляді системи лінійних рівнянь.
,
у вигляді системи лінійних рівнянь.Розв’язати систему:
а) матричним методом;
б) за формулами Крамера;
в) методом Гаусса.
Розв’язання.
1. Транспонуємо матрицю
 :
:

і
знайдемо матриці
 ,
, ,
, і
і :
:
 ;
;
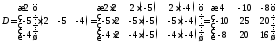 ;
;
 ;
;



2. Запишемо
матричне рівняння
 :
:

і виконаємо множення матриць в лівій частині рівняння

З рівності матриць однакового розміру маємо систему лінійних рівнянь

Розв’яжемо отриману систему вказаними в умові методами:
а) матричним методом.
Розв’язком
матричного рівняння
 є матриця
є матриця ,
де
,
де - обернена матриця, яка обчислюється за
формулою
- обернена матриця, яка обчислюється за
формулою
 .
.
Обчислимо визначник системи

Оскільки
 ,
то обернена матриця існує. Обчислимо
її елементи
,
то обернена матриця існує. Обчислимо
її елементи - алгебраїчні доповнення елементів
матриці
- алгебраїчні доповнення елементів
матриці .
.
 ,
,
 ,
, ,
,
 ,
,  ,
, ,
,
 ,
,
 ,
, .
.
Запишемо
обернену матрицю
 і знайдемо розв’язок
системи:
і знайдемо розв’язок
системи:
 ,
,
 .
.
Остаточно
маємо
 .
Звідки
.
Звідки ,
,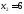 ,
,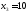 .
.
б) Розв’яжемо систему за формулами Крамера.
Оскільки головний визначник системи вже обчислено, то обчислимо допоміжні визначники:
 ;
;
 ;
;
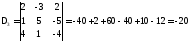 ;
;
За формулами
Крамера отримаємо наступний розв’язок
системи ( ):
):
 ;
;
 ;
; .
.
в) Розв’яжемо систему методом Гаусса.
Поміняємо місцями перше та друге рівняння:
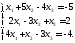
Нове перше
рівняння системи приймемо за перше
ведуче рівняння системи. Виключимо
 з другого і третього рівнянь. Для цього
помножимо перше рівняння на
з другого і третього рівнянь. Для цього
помножимо перше рівняння на і
і і по черзі додамо до другого і третього
рівнянь.
і по черзі додамо до другого і третього
рівнянь.

Отримаємо

Поділимо
друге рівняння на
 і приймемо його за друге ведуче рівняння:
і приймемо його за друге ведуче рівняння:

Виключимо
 з третього рівняння. Для цього помножимо
друге рівняння на 19 і додамо до третього:
з третього рівняння. Для цього помножимо
друге рівняння на 19 і додамо до третього:
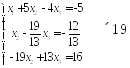

Прямий
хід метода Гаусса закінчено. Обернений
хід: з третього рівняння знаходимо
 ,
з другого -
,
з другого - ,
з першого -
,
з першого - :
:

Розв’язок
системи:
 .
.
Відповідь.
 ,
, ,
, .
.
Завдання 2.
Задано
вектори
 .
. ,
, ,
, у деякому базисі. Показати, що вектори
у деякому базисі. Показати, що вектори ,
, ,
, утворюють базис та знайти координати
вектора
утворюють базис та знайти координати
вектора у цьому базисі.
у цьому базисі.
Розв’язання.
Вектори
 ,
, ,
, утворюють базис у тривимірному просторі,
якщо вони некомпланарні. Щоб перевірити
це, знайдемо мішаний добуток цих векторів:
утворюють базис у тривимірному просторі,
якщо вони некомпланарні. Щоб перевірити
це, знайдемо мішаний добуток цих векторів:
 .
.
Оскільки
 ,
то вектори
,
то вектори ,
, ,
, некомпланарні і утворюють базис, в якому
вектор
некомпланарні і утворюють базис, в якому
вектор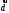 матиме розклад
матиме розклад
 (2.1)
(2.1)
або
 ,
,
де
 ,
, ,
, - координати вектора
- координати вектора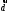 в цьому базисі. Для їх обчислення складемо
систему рівнянь:
в цьому базисі. Для їх обчислення складемо
систему рівнянь:
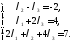
Розв’яжемо
систему за формулами Крамера:
 ,
, ,
,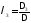 .
.
 ,
,
 ,
,
 ,
,
 .
.
Отже,
 ,
, ,
, .
.
Підставимо
 ,
, ,
,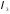 у формулу (2.1) і одержимо розкладання
вектора
у формулу (2.1) і одержимо розкладання
вектора :
:
 .
.
Відповідь.
Вектори
 ,
, ,
, утворюють базис у тривимірному просторі.
Вектор
утворюють базис у тривимірному просторі.
Вектор в цьому базисі має розклад
в цьому базисі має розклад .
.
Завдання 3.
Задано
координати вершин піраміди
 :
: ,
,
 ,
, .
Знайти:
.
Знайти:
1)
кут між ребром
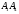 та гранню
та гранню ;
;
2)
площу грані
 ;
3) об’єм піраміди;
;
3) об’єм піраміди;
4)
рівняння висоти, яку проведено з вершини
 до грані
до грані .
.
Розв’язання.
1) Синус кута між ребром
 та гранню
та гранню обчислимо за формулою
обчислимо за формулою
 ,
(3.1)
,
(3.1)
де
 ,
, ,
, - координати нормального вектора площини
(грані
- координати нормального вектора площини
(грані ),
а
),
а ,
, ,
, - координати напрямного вектора прямої
- координати напрямного вектора прямої .
.
Складемо
рівняння грані
 як рівняння площини, що проходить через
три точки
як рівняння площини, що проходить через
три точки ,
, ,
, :
:
 .
(3.2)
.
(3.2)
Підставимо
в рівняння (3.2) координати точок
 ,
, ,
, :
:
 або
або
 .
.
Розкладаючи визначник за елементами першого рядка, отримаємо:
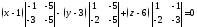 ,
,
 ,
,
 ,
,
 ,
,
 .
.
З рівняння площини запишемо координати її нормального вектора
 .
.
Складемо
рівняння ребра
 як рівняння прямої, що проходить через
точки
як рівняння прямої, що проходить через
точки і
і :
:
 .
.
Отримаємо
 або
або
 .
.
З цього
рівняння маємо координати напрямного
вектора ребра
 :
: ,
, ,
, .
.
Підставляючи знайдені координати нормального і напрямного векторів у формулу (3.1), дістанемо
 ,
,
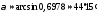 .
.
2) Площу
грані
 знайдемо за формулою
знайдемо за формулою
 ,
,
де
координати векторів
 і
і знайдемо, віднімаючи від координат
кінця координати початку:
знайдемо, віднімаючи від координат
кінця координати початку: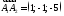 ,
,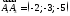 .
.
 ,
,
 ,
,
 .
.
3) Об’єм піраміди обчислимо за формулою
 ,
,
де
 ,
, .
Таким чином,
.
Таким чином,
 ,
,
 .
.
4) Рівняння
висоти, яку проведено з вершини
 до грані
до грані ,
отримаємо за формулою
,
отримаємо за формулою
 ,
,
де
 ,
, ,
, - координати напрямного вектора висоти.
- координати напрямного вектора висоти.
Оскільки
висота піраміди, яку проведено з вершини
 ,
паралельна нормальному вектору площини
,
паралельна нормальному вектору площини ,
то координати останнього можна прийняти
за координати напрямного вектора висоти,
тобто
,
то координати останнього можна прийняти
за координати напрямного вектора висоти,
тобто ,
, ,
, .
Тоді рівняння висоти матиме вигляд
.
Тоді рівняння висоти матиме вигляд
 або
або
 .
.
Відповідь.
1)
 ;
2)
;
2)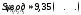 ;
;
3)
 ;
4)
;
4) .
.
Завдання 4.
Скласти
рівняння лінії, для якої відстані кожної
точки від точки
 і від прямої
і від прямої відносяться як
відносяться як .
.
Розв’язання.
Нехай
 -довільна
точка лінії, рівняння якої треба скласти.
За умовою задачі
-довільна
точка лінії, рівняння якої треба скласти.
За умовою задачі
 ,
де
,
де ,
, .
.







Отже, маємо рівняння
 або
або
 .
.
Перетворимо його:
 ,
,
 ,
,
 ,
,
 .
.
Для
доданків з
 виділимо повний квадрат:
виділимо повний квадрат:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Отримали
рівняння гіперболи з центром у точці
 і півосями
і півосями ,
, .
.
Відповідь.
 - рівняння гіперболи з центром у точці
- рівняння гіперболи з центром у точці і півосями
і півосями ,
, .
.
