
Екзамен з вищ / Екзамен з вищ.мат-1 / 4 / Функ_1
.doc
-
Диференціальне числення
функцій декількох змінних
-
Теоретичні питання
4.1.1. Поняття функції декількох змінних. Область визначення, границя і неперервність функції декількох змінних.
4.1.2. Частинні похідні функції декількох змінних, похідна в напрямі, градієнт.
4.1.3. Диференційованість і повний диференціал функції декількох змінних. Застосування повного диференціала до наближених обчислень.
4.1.4. Геометричний зміст повного диференціала. Дотична площина та нормаль до поверхні.
4.1.5. Похідні складеної функції декількох змінних. Повна похідна. Похідні функцій, заданих неявно.
4.1.6. Частинні похідні та повні диференціали вищих порядків. Незалежність результату від порядку диференціювання.
4.1.7. Формула Тейлора для функції декількох змінних.
4.1.8. Екстремум функції декількох змінних. Необхідні та достатні умови екстремуму. Найменше та найбільше значення функції декількох змінних в обмеженій замкненій області.
4.1.9. Умовний екстремум функції декількох змінних.
4.1.10. Метод найменших квадратів. Побудова емпіричної формули у випадку, коли шукана функція є лінійною.
-
Тестові теоретичні завдання
4.2.1. Функція
![]() зображається графічно:
зображається графічно:
а) деякою лінією в просторі ;
б) деякою лініює на площині;
в) деякою поверхнею в просторі ;
г) деякою областю на площині ; д) інша відповідь.
4.2.2. Вставити пропущений
вираз. Означення границі функції:
Число
![]() називається границею функції
називається границею функції
![]() в точці
в точці
![]() ,
якщо _____________________, що для всіх точок
,
якщо _____________________, що для всіх точок
![]() таких, що
таких, що
![]() виконується нерівність
виконується нерівність
![]() .
.
а) для будь-якого
![]() ,
для будь-якого
,
для будь-якого
![]() ;
;
б) для будь-якого
![]() існує таке
існує таке
![]() ;
;
в) існує таке
![]() ,
існує таке
,
існує таке
![]() ;
;
г) існує таке
![]() ,
що для будь-якого
,
що для будь-якого
![]() ;
;
д) інша відповідь.
4.2.3. Точка
![]() є точкою розриву функції
є точкою розриву функції
![]() ,
якщо із умов:
,
якщо із умов:
-
Функція визначена в точці
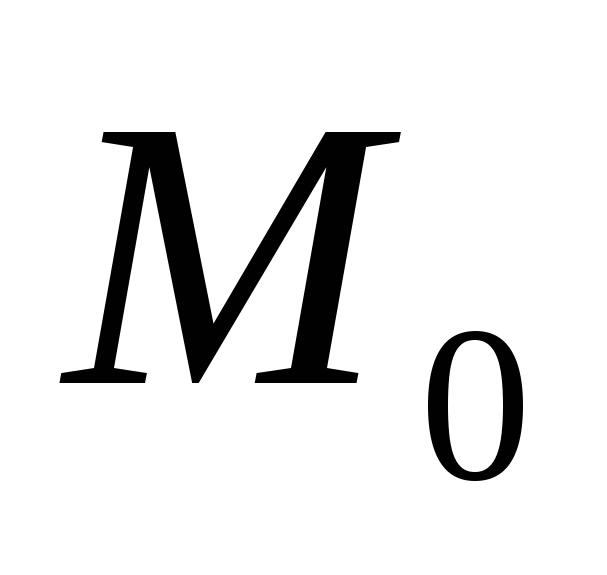 .
. -
Існує
 .
. -
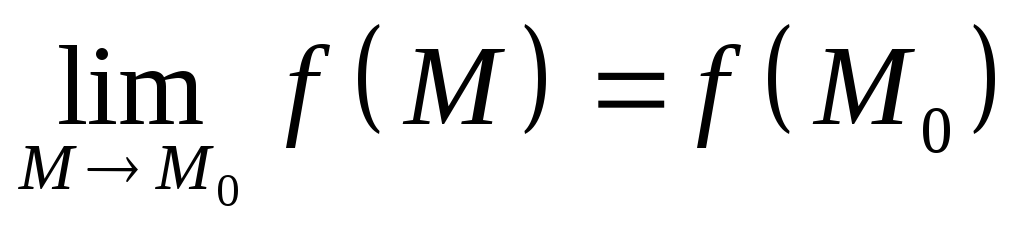 .
.
порушується:
а) тільки 1; б) тільки 2; в) тільки 3;
г) хоча б одна; д) інша відповідь.
-
Якщо функція
 неперервна в обмеженій замкненій
області
неперервна в обмеженій замкненій
області
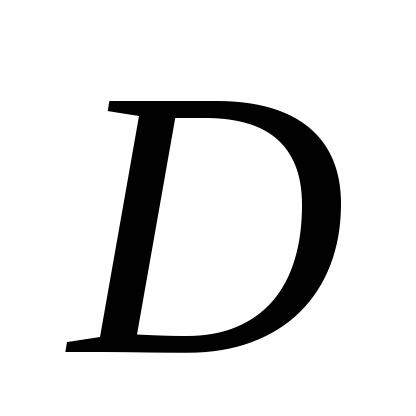 ,
то вона там:
,
то вона там:
а) обмежена ; б) додатна ; в) необмежена;
г) постійна ; д) інша відповідь.
-
Яка з наведених нижче рівностей завжди виконується для функції
 при умові, що відповідні похідні
неперервні.
при умові, що відповідні похідні
неперервні.
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
-
Повний диференціал функції
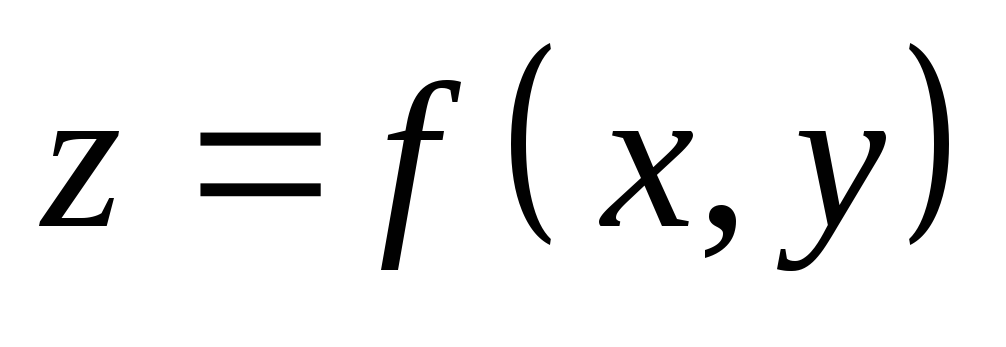 знаходиться за формулою:
знаходиться за формулою:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д) інша відповідь.
-
Яка з наступних формул використовується в наближених обчисленнях?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
-
Яке з рівнянь визначає дотичну площину до поверхні
 в точці
в точці
 ?
?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д) інша відповідь.
-
Яке з рівнянь визначає нормаль до поверхні
 в точці
в точці
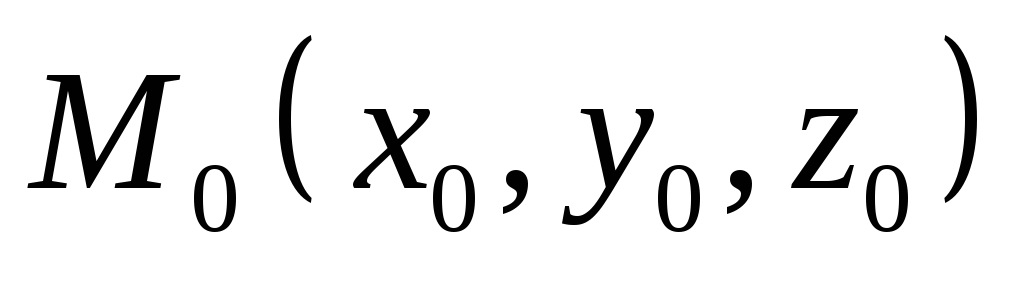 ?
?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
-
Яке з рівнянь визначає дотичну площину до поверхні, заданої рівнянням
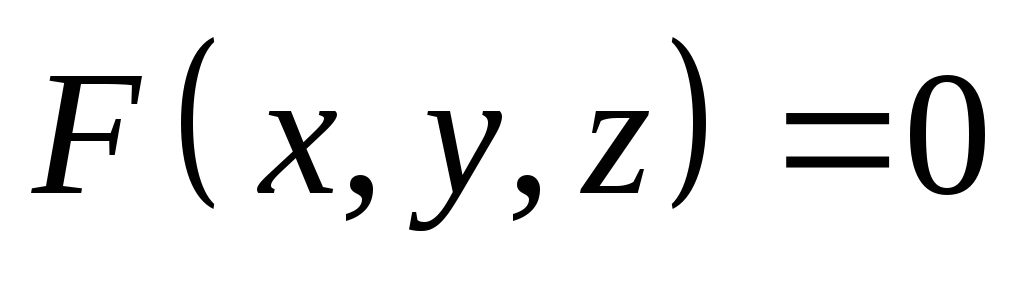 ,
в точці
,
в точці
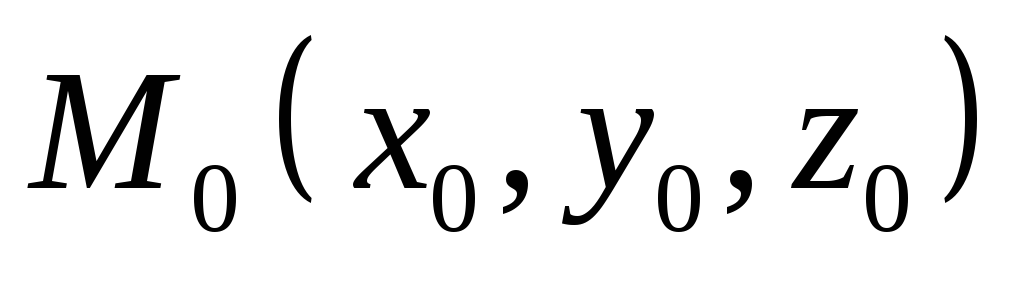 ?
?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д) інша відповідь.
4.2.11. Яке з рівнянь визначає
нормаль до поверхні, заданої рівнянням
![]() в точці
в точці
![]() ?
?
а)
![]()
б)
![]()
в)
![]()
г)
![]() д) інша відповідь.
д) інша відповідь.
4.2.12. Якщо
![]() ,
де
,
де
![]() ,
то яка з рівностей є правильною:
,
то яка з рівностей є правильною:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.13. Якщо
![]() ,
де
,
де
![]() ,
то яка з рівностей є правильною:
,
то яка з рівностей є правильною:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.14. Якщо
![]() ,
де
,
де
![]() ,
то яка з рівностей є правильною:
,
то яка з рівностей є правильною:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.15. Якщо
![]() ,
де
,
де
![]() ,
то яка з рівностей є правильною:
,
то яка з рівностей є правильною:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.16. Яка з формул є правильною,
якщо неявна функція однієї змінної
задана рівнянням
![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.17. Яка з формул є правильною,
якщо неявна функція двох змінних задана
рівнянням
![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.18. Яка з формул є правильною,
якщо неявна функція двох змінних задана
рівнянням
![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.19. Градієнтом функції
![]() називається:
називається:
а) скаляр
 ;
;
б) вектор
![]() ;
;
в) вектор
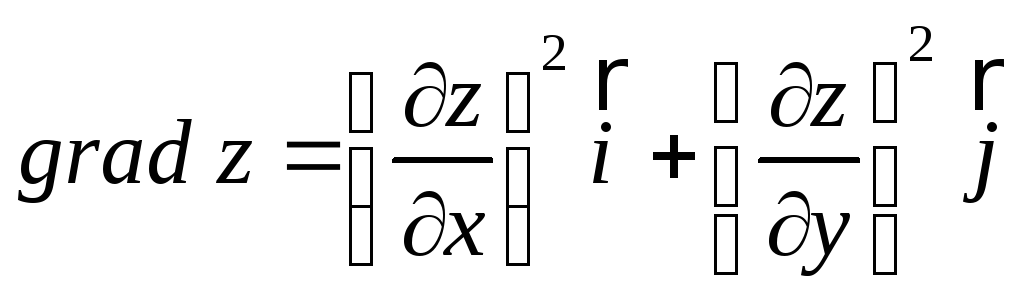 ;
;
г) скаляр
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.20. Градієнтом функції
![]() називається:
називається:
а) вектор![]() ;
;
б) скаляр
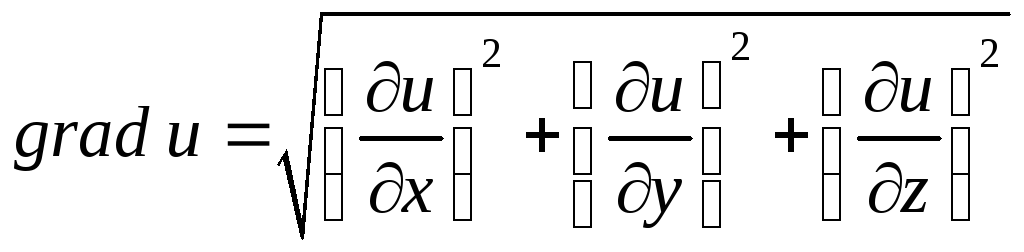 ;
;
в) скаляр
![]() ;
;
г) вектор
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.21. Похідна функції
![]() за напрямом вектора
за напрямом вектора
![]() ,
який складає кути
,
який складає кути
![]() і
і
![]() з координатними осями
знаходиться за формулою:
з координатними осями
знаходиться за формулою:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.22. Похідна функції
![]() за напрямом вектора
за напрямом вектора
![]() ,
який складає кути
,
який складає кути
![]() ,
,
![]() і
і
![]() з координатними осями знаходиться за
формулою:
з координатними осями знаходиться за
формулою:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.23. Повний диференціал
![]() -го
порядку функції
-го
порядку функції
![]() знаходиться за формулою:
знаходиться за формулою:
а)
![]() ;
б)
;
б)
 ;
;
в)
 ;
г)
;
г)
![]() ;
;
д) інша відповідь.
4.2.24. Повний диференціал
другого порядку функції
![]() знаходиться за формулою:
знаходиться за формулою:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.25. Повний диференціал
третього порядку функції
![]() знаходиться за формулою:
знаходиться за формулою:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д) інша відповідь.
4.2.26. Функція
![]() має неперервні частинні похідні до
четвертого порядку включно. Які з поданих
нижче похідних співпадають?
має неперервні частинні похідні до
четвертого порядку включно. Які з поданих
нижче похідних співпадають?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() .
.
а) 1 і 4, 2 і 5, 3 і 6 ; б) 1 і 5, 2 і 4, 3 і 6 ;
в) 1 і 6, 2 і 5, 3 і 4 ;
г) 1 і 3, 2 і 4, 5 і 6 ; д) інша відповідь.
4.2.27. Функція
![]() має неперервні частинні похідні до
п’ятого порядку включно. Які з поданих
нижче похідних співпадають?
має неперервні частинні похідні до
п’ятого порядку включно. Які з поданих
нижче похідних співпадають?
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
а) 1 і 2, 3 і 4, 5 і 6; б)1 і 5, 2 і 6, 3 і 4;
в) 1 і 4, 2 і 5, 3 і 6;
г) 1 і 6, 2 і 4, 3 і 5; д) інша відповідь.
4.2.28. Стаціонарною точкою
функції
![]() називається точка
називається точка
![]() ,
в якій:
,
в якій:
а)
![]() не існує,
не існує,
![]() ;
;
б)
![]() ,
,
![]() не існує ;
не існує ;
в)
![]() ,
,
![]() не існують ;
не існують ;
г)
![]() ,
,
![]() ;
д) інша відповідь.
;
д) інша відповідь.
4.2.29. Нехай функція
![]() має в деякому околі точки
має в деякому околі точки
![]() неперервні частинні похідні першого і
другого порядків, причому
неперервні частинні похідні першого і
другого порядків, причому
![]() .
Тоді функція має в точці
.
Тоді функція має в точці
![]() екстремум, якщо:
екстремум, якщо:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д) інша відповідь.
4.2.30. Нехай функція
![]() має в деякому околі точки
має в деякому околі точки
![]() неперервні частинні похідні першого і
другого порядків, причому
неперервні частинні похідні першого і
другого порядків, причому
![]() .
Тоді функція має в точці
.
Тоді функція має в точці
![]() максимум, якщо:
максимум, якщо:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д) інша відповідь.
4.2.31. Нехай функція
![]() має в деякому околі точки
має в деякому околі точки
![]() неперервні частинні похідні першого і
другого порядків, причому
неперервні частинні похідні першого і
другого порядків, причому
![]() .
Тоді функція має в точці
.
Тоді функція має в точці
![]() мінімум, якщо:
мінімум, якщо:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д) інша відповідь.
4.2.32. Нехай функція
![]() має в деякому околі точки
має в деякому околі точки
![]() неперервні частинні похідні першого і
другого порядків, причому
неперервні частинні похідні першого і
другого порядків, причому
![]() .
Тоді функція не має в точці
.
Тоді функція не має в точці
![]() екстремуму, якщо:
екстремуму, якщо:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д) інша відповідь.
4.2.33. Формула
Тейлора для функції
![]() має вид:
має вид:
а)
![]()
![]() ;
;
б)
![]()
![]() ;
;
в)
![]()
![]() ;
;
г)
![]()
![]() ;
;
д) інша відповідь.
4.2.34. При знаходженні екстремуму
функції
![]() при умові
при умові
![]() складається функція Лагранжа
складається функція Лагранжа
![]() ,
яка має вид:
,
яка має вид:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д) інша відповідь.
4.2.35. Координати точок,
підозрілих на екстремум функції
![]() при умові
при умові
![]() знаходяться із системи рівнянь:
знаходяться із системи рівнянь:
а)
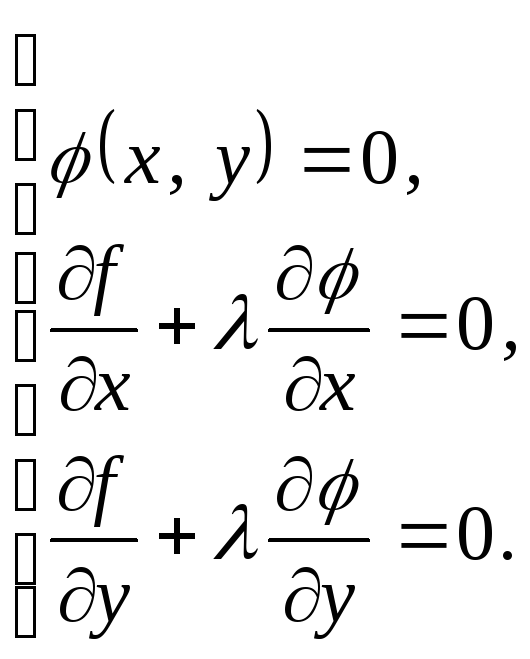 б)
б)
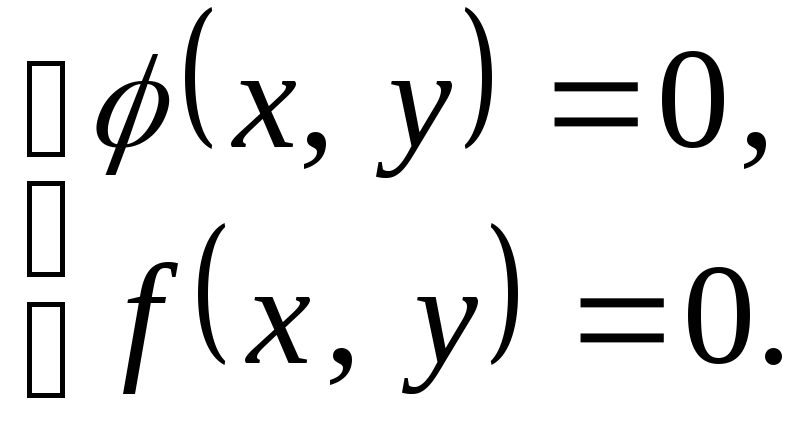 в)
в)

г)
 д) інша відповідь.
д) інша відповідь.
