
- •3 Комплексні числа. Многочлени. Інтегральне числення функцій однієї змінної
- •3.1 Теоретичні питання
- •3.1.10. Інтегрування ірраціональних функцій. Розглянути інтеграли .
- •3.1.14. Інтегрування тригонометричних функцій спеціального виду. Розглянути інтеграли .
- •3.2 Тестові теоретичні завдання
- •3.3 Тестові практичні завдання
3 Комплексні числа. Многочлени. Інтегральне числення функцій однієї змінної
3.1 Теоретичні питання
3.1.1. Поняття комплексного числа. Різні форми представлення комплексних чисел. Дії над комплексними числами в алгебраїчній і тригонометричній формах.
3.1.2. Многочлени в комплексній області. Теорема Безу. Основна теорема алгебри. Умова тотожності двох многочленів.
3.1.3. Дійсні многочлени. Розклад дійсного многочлена на лінійні і квадратичні множники.
3.1.4. Поняття про первісну. Теорема про зв’язок між первісними. Означення невизначеного інтеграла.
3.1.5. Таблиця основних інтегралів. Правильність формул перевірити диференціюванням. Безпосереднє інтегрування.
3.1.6. Метод підстановки та метод інтегрування частинами у невизначеному інтегралі.
3.1.7. Інтегрування елементарних раціональних дробів.
3.1.8. Розклад раціонального дробу на елементарні. Інтегрування раціональних функцій.
3.1.9. Інтегрування ірраціональних
функцій. Розглянути інтеграли

![]() ,
,
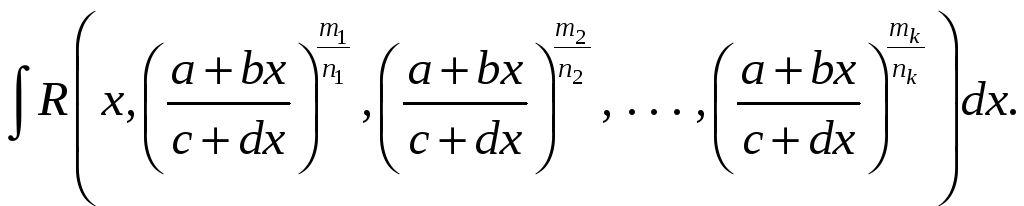
3.1.10. Інтегрування ірраціональних функцій. Розглянути інтеграли .
3.1.11. Інтегрування ірраціональних
функцій за допомогою тригонометричних
підстановок. Розглянути інтеграли
![]()
![]() .
.
3.1.12. Інтегрування тригонометричних функцій (загальний випадок). Універсальна підстановка. Окремі випадки.
3.1.13. Інтегрування тригонометричних
функцій спеціального виду. Розглянути
інтеграли
![]()
![]() .
.
3.1.14. Інтегрування тригонометричних функцій спеціального виду. Розглянути інтеграли .
3.1.15. Задачі, які приводять до поняття визначеного інтеграла.
3.1.16. Означення визначеного інтеграла. Умови інтегровності функції. Властивості визначеного інтеграла.
3.1.17. Поняття про визначений інтеграл із змінною верхньою межею. Теорема про похідну визначеного інтеграла по його верхній межі.
3.1.18. Теорема про похідну визначеного інтеграла по його верхній межі. Формула Ньютона- Лейбніца.
3.1.19. Заміна змінної у визначеному інтегралі. Інтегрування частинами.
3.1.20. Невласні інтеграли ( 1-го і 2-го роду ).
3.1.21. Застосування визначеного інтеграла у геометричних задачах.
3.1.22. Застосування визначеного інтеграла у задачах фізики та механіки.
3.2 Тестові теоретичні завдання
3.2.1. Які з наведених нижче рівностей є правильними:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
а) 1 і 2; б) 2 і 3; в) 1 і 4;
г)2 і 4; д) інша відповідь.
3.2.2. Які з наведених нижче рівностей не є правильними:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
а) 1 і 2; б) 2 і 3; в) 2 і 4;
г) 1 і 4; д) інша відповідь.
3.2.3. Модуль комплексного числа
![]() обчислюється за формулою:
обчислюється за формулою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.4. Спряженим до комплексного
числа
![]() є число:
є число:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.5. Дійсною частиною добутку
комплексних чисел
![]() та
та
![]() є:
є:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.6. Уявною частиною добутку
комплексних чисел
![]() та
та
![]() є:
є:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.7. Дійсною частиною частки
від ділення комплексного числа
![]() на число
на число![]() є:
є:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.8. Уявною частиною частки
від ділення комплексного числа
![]() на число
на число![]() є:
є:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.9. Сума комплексного числа
![]() із спряженим
із спряженим
![]() дорівнює:
дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.10. Добуток комплексного
числа
![]() на спряжене
на спряжене
![]() дорівнює:
дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д) інша відповідь.
3.2.11. При множенні комплексних чисел в тригонометричній формі
1) аргументи множаться; 2) модулі множаться;
3) аргументи додаються; 4) модулі додаються.
Із наведених тверджень правильними є:
а) 1 і 4; б) 1і 2; в) 2 і 3;
г) 3 і 4; д) інша відповідь.
3.2.12. При діленні комплексних чисел у тригонометричній формі
1) модулі віднімаються; 2) модулі діляться;
3) аргументи діляться; 4 ) аргументи віднімаються,
Із наведених тверджень правильними є:
а) 1 і 3; б) 1 і 4; в) 2 і 3;
г) 2 і 4; д) інша відповідь.
3.2.13. Якщо
![]() ,
то (
,
то (![]() - натуральне):
- натуральне):
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Із наведених рівностей правильними є:
а) 1 і 2; б) 1 і 3; в) 2 і 4;
г) 3 і 4; д) інша відповідь.
3.2.14. Якщо комплексне число
![]() є коренем многочлена з дійсними
коефіцієнтами
є коренем многочлена з дійсними
коефіцієнтами
![]() , то цей многочлен ділиться без остачі
на:
, то цей многочлен ділиться без остачі
на:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.15. Якщо многочлен
![]() з дійсними коефіцієнтами має два дійсних
корені і один комплексний, то степінь
з дійсними коефіцієнтами має два дійсних
корені і один комплексний, то степінь
![]() цього многочлена не може дорівнювати:
цього многочлена не може дорівнювати:
а) 4; б) 6; в) 3; г) 5; д) інша відповідь.
3.2.16. Якщо многочлен
![]() з дійсними коефіцієнтами має двократний
дійсний корінь і простий комплексний
корінь, то степінь
з дійсними коефіцієнтами має двократний
дійсний корінь і простий комплексний
корінь, то степінь
![]() цього многочлена не може дорівнювати:
цього многочлена не може дорівнювати:
а) 4; б) 6; в) 3; г) 5; д) інша відповідь.
3.2.17. Якщо многочлен
![]() з дійсними коефіцієнтами має двократний
дійсний і двократний комплексний корені,
то яка з рівностей, наведених нижче,
можлива для степеня цього многочлена:
з дійсними коефіцієнтами має двократний
дійсний і двократний комплексний корені,
то яка з рівностей, наведених нижче,
можлива для степеня цього многочлена:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.18. Вставити пропущене слово.
Функція, похідна якої на деякому проміжку дорівнює нулю, _____________ на цьому проміжку.
а) від’ємна; б) додатна; в)стала;
г) змінна; д) інша відповідь.
3.2.19. Вставити пропущене слово.
Множина всіх первісних для
функції
![]() називається ________ інтегралом.
називається ________ інтегралом.
а) визначеним; б) невизначеним;
в) невласним 1-го роду; г) невласним 2-го роду;
д) інша відповідь.
3.2.20. Вставити пропущене слово.
___________ множник можна виносити за знак невизначеного інтеграла.
а) Cталий; б) Змінний; в) Нормуючий;
г) Загальний; д) інша відповідь.
3.2.21. Вставити пропущені слова.
Границю __________ ( число
![]() ) називають визначеним інтегралом для
функції
) називають визначеним інтегралом для
функції
![]() на відрізку
на відрізку
![]() і позначають
і позначають
![]() .
.
а) функції
![]() ;
б) відношення приросту функції до
приросту аргумента;
;
б) відношення приросту функції до
приросту аргумента;
в) інтегральної суми; г) диференціальної суми; д) інша відповідь.
3.2.22. Вставити пропущене слово.
Якщо функція
![]() інтегрована на відрізку
інтегрована на відрізку
![]() ,
то вона _____________ на цьому відрізку.
,
то вона _____________ на цьому відрізку.
а) монотонна; б) неперервна; в) диференційована;
г) обмежена; д) інша відповідь.
3.2.23. Вставити пропущене слово.
___________ множник можна виносити за знак визначеного інтеграла.
а) Додатний; б) Цілий; в) Сталий;
г) Змінний; д) інша відповідь.
3.2.24. Вставити пропущене слово.
Нехай функція
![]() визначена на
визначена на
![]() і інтегрована на
і інтегрована на
![]() ,
де
,
де
![]() - довільне число, більше за
- довільне число, більше за
![]() .
Тоді інтеграл
.
Тоді інтеграл![]() називається ______.
називається ______.
а) невласним 1-го роду; б) невласним 2-го роду;
в) невизначеним;
г) із змінною верхньою межею; д) інша відповідь.
3.2.25. Вставити пропущений вираз.
Дослідження на збіжність невласного інтеграла 1-го роду зводиться до знаходження __________.
а) визначеного інтеграла
![]() ;
;
б) диференціала
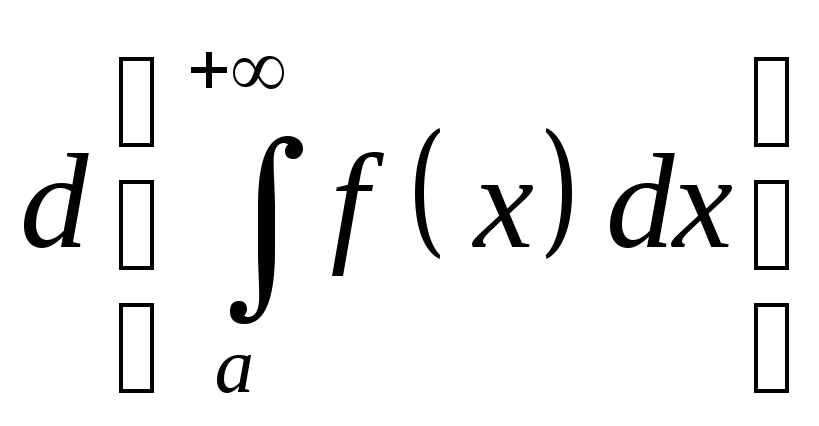 ;
в) границі
;
в) границі
![]() ;
;
г) границі
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.26. Якщо функція
![]() має первісну, то цих первісних:
має первісну, то цих первісних:
а) одна; б) дві; в) скінченне число; г) безліч; д) інша відповідь.
3.2.27. Якщо
![]() і
і
![]() - дві первісні для функції
- дві первісні для функції
![]() ,
то чому дорівнює різниця
,
то чому дорівнює різниця
![]() ?
?
а) 0; б) сталій
![]() ;
в) деякій функції
;
в) деякій функції
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.28. Результат інтегрування перевіряється за допомогою операції:
а) диференціювання; б) повторного інтегрування;
в) піднесення до степеня;
г) множення на підінтегральну функцію;
д) інша відповідь.
3.2.29. Похідна невизначеного інтеграла дорівнює:
а) підінтегральному виразу;
б) підінтегральній функції;
в) первісній; г) сталій; д) інша відповідь.
3.2.30. Вставити пропущене слово.
Невизначений інтеграл від суми функцій дорівнює __________ невизначених інтегралів від кожної функції.
а) добутку; б) частці; в) різниці;
г) сумі; д) інша відповідь.
3.2.31. Заміна змінної у невизначеному інтегралі може відбуватись за схемою:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д) інша відповідь.
3.2.32. Який із вказаних інтегралів береться частинами:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.33. Який із вказаних інтегралів береться частинами:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.34. Який із вказаних інтегралів береться частинами:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.35. Який із вказаних інтегралів не береться частинами:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.36. Який із вказаних інтегралів не береться частинами:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.37. Функція
![]() буде дробово -
раціональною, якщо:
буде дробово -
раціональною, якщо:
а)
![]() і
і
![]() - довільні функції;
- довільні функції;
б)
![]() і
і
![]() - довільні многочлени;
- довільні многочлени;
в)
![]() - довільна функція,
- довільна функція,
![]() - многочлен;
- многочлен;
г)
![]() - многочлен,
- многочлен,
![]() - довільна функція;
- довільна функція;
д) інша відповідь.
3.2.38. Раціональний дріб
![]() вважається правильним, якщо степені
многочленів:
вважається правильним, якщо степені
многочленів:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.39. Правильний раціональний дріб інтегрується шляхом:
а) розкладання чисельника на множники;
б) розкладання чисельника і знаменника на множники;
в) розкладання раціонального дробу на суму елементарних дробів;
г) ділення чисельника і знаменника на старший степінь;
д) інша відповідь.
3.2.40. Інтеграл
 раціоналізується підстановкою
раціоналізується підстановкою
![]() ,
де
,
де
![]() :
:
а) найбільше з чисел![]() ;
;
б) найменше з чисел
![]() ;
;
в) сума чисел
![]() ;
;
г) спільний знаменник дробів
![]() ;
;
д) інша відповідь.
3.2.41. Інтеграл
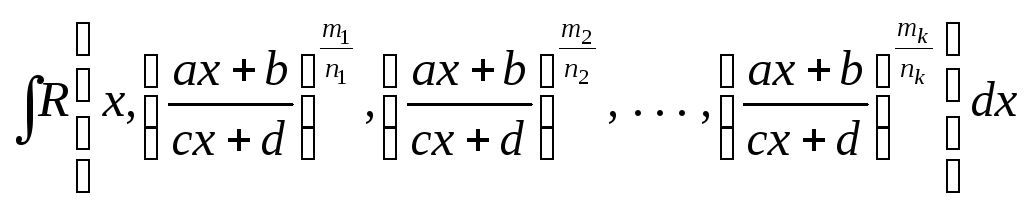 раціоналізується підстановкою
раціоналізується підстановкою
![]() ,
де
,
де
![]() :
:
а) найменше з чисел
![]() ;
;
б) найбільше з чисел
![]() ;
;
в) найменше спільне кратне
чисел
![]() ;
;
г) сума чисел
![]() ;
;
д) інша відповідь.
3.2.42. Інтеграл
![]() ,
де
,
де
![]() ,
,
![]() - ціле, раціоналізується підстановкою:
- ціле, раціоналізується підстановкою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.43. Інтеграл
![]() ,
де
,
де
![]() ,
,
![]() - ціле, раціоналізується підстановкою:
- ціле, раціоналізується підстановкою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.44. Інтеграл
![]() зводиться до табличного шляхом:
зводиться до табличного шляхом:
а) виділення під коренем повного квадрату;
б)
піднесення до
квадрата; в)
заміни
![]() ;
;
г) інтегрування частинами; д) інша відповідь.
3.2.45. Інтеграл
![]() береться за допомогою підстановки:
береться за допомогою підстановки:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.46. В інтегралі
![]() використовується
підстановка виду:
використовується
підстановка виду:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.47. Яка з вказаних задач не приводить до поняття визначеного інтеграла:
а) задача про площу криволінійної трапеції;
б) задача про кутовий коефіцієнт дотичної до кривої;
в) задача про масу неоднорідного лінійного стержня;
г) задача про роботу змінної сили; д) інша відповідь.
3.2.48. Інтеграл
![]() дорівнює:
дорівнює:
а) 1;
б)
![]() ;
в)
;
в)
![]() ;
г) 0; д) інша відповідь.
;
г) 0; д) інша відповідь.
3.2.49. Якщо функція
![]() є неперервною на
є неперервною на
![]() ,
то функція
,
то функція
![]() є диференційованою в кожній точці цього
відрізка і похідна
є диференційованою в кожній точці цього
відрізка і похідна
![]() дорівнює:
дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г) 0; д) інша відповідь.
;
г) 0; д) інша відповідь.
3.2.50. Невласний інтеграл 1-го
роду
![]() буде збіжним, якщо буде збіжним:
буде збіжним, якщо буде збіжним:
а) кожний з інтегралів
![]() ;
;
б) хоча б один з інтегралів
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.51. Щоб інтеграл
![]() був невласним 2-го роду підінтегральна
функція
був невласним 2-го роду підінтегральна
функція
![]() на
на
![]() має бути:
має бути:
а) обмеженою; б) необмеженою; в) визначеною;
г) неперервною; д) інша відповідь.
3.2.52. Яка з наведених формул не належить до формул наближеного обчислення визначеного інтеграла:
а) формула прямокутників; б) формула трапецій;
в) формула Ньютона-Лейбніца;
г) формула Симпсона; д) інша відповідь.
3.2.53. Функція
![]() називається первісною для функції
називається первісною для функції
![]() на множині
на множині
![]() ,
якщо для всіх
,
якщо для всіх
![]() виконується рівність:
виконується рівність:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.54. Нехай
![]() і
і
![]() - первісні для функції
- первісні для функції
![]() на
на
![]() .
Тоді на
.
Тоді на
![]() :
:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.55. Інтегрування частинами у невизначеному інтегралі відбувається за формулою:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.56. Якщо поміняти місцями межі інтегрування у визначеному інтегралі, то:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.57. Для будь-яких чисел
![]() має місце рівність:
має місце рівність:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.58. Якщо
![]()
![]() - відповідно найменше і найбільше
значення функції
- відповідно найменше і найбільше
значення функції
![]() на відрізку
на відрізку
![]() ,
то:
,
то:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.59. Теорема про середнє. Якщо
функція
![]() неперервна на відрізку
неперервна на відрізку
![]() ,
то знайдеться точка
,
то знайдеться точка
![]() така, що:
така, що:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д) інша відповідь.
3.2.60. Теорема. Нехай виконані умови:
1)
![]() є неперервною функцією на
є неперервною функцією на
![]() ;
;
2) функція
![]() і її похідна
і її похідна
![]() є неперервними на
є неперервними на
![]() %
%
3)
![]() і значення
і значення
![]() не виходять за межі
не виходять за межі
![]() при
при
![]() .
.
Тоді справджується рівність:
а)
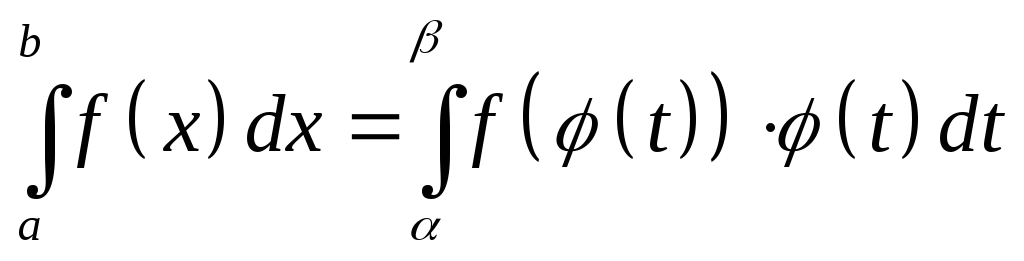 ;
б)
;
б)
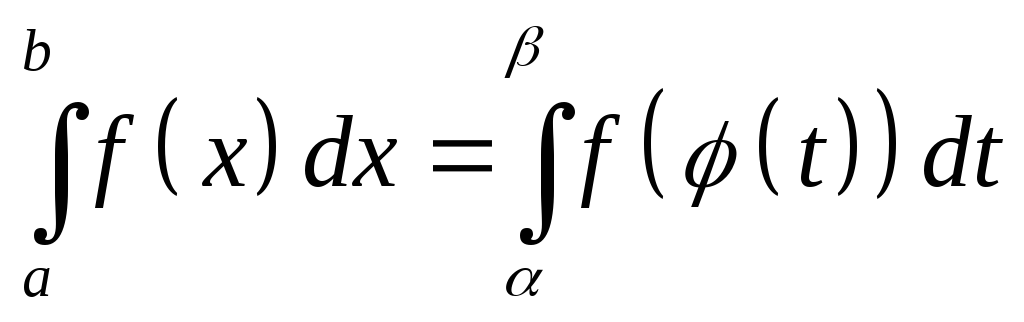 ;
;
в)
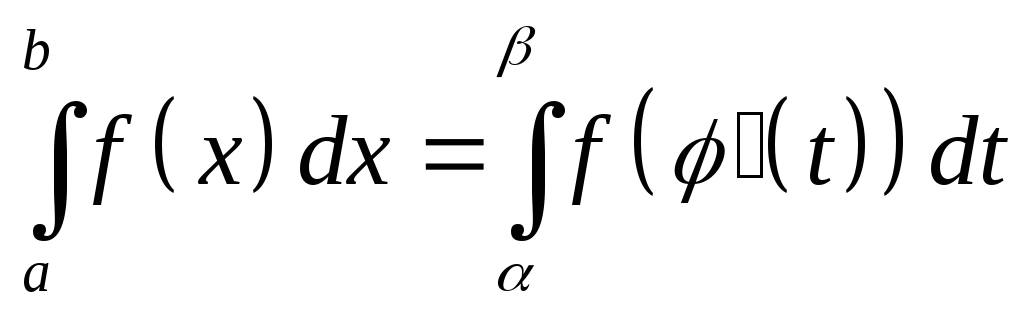 ;
г)
;
г)
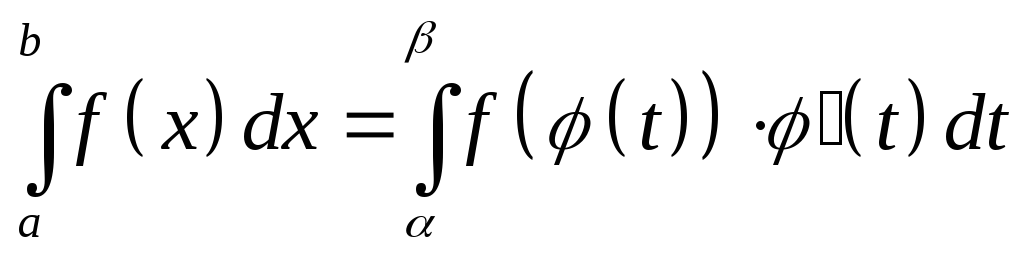 ;
;
д) інша відповідь.
3.2.61. Формула Ньютона-Лейбніца має вид:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д) інша відповідь.
3.2.62. Нехай функції
![]() неперервні разом із своїми похідними
на
неперервні разом із своїми похідними
на
![]() .
.
Тоді формула інтегрування частинами для визначеного інтеграла має вид:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.63. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-1, 2-3, 3-2; б) 1-2, 2-1, 3-3; в) 1-3, 2-2, 3-1;
г) 1-1, 2-2, 3-3; д) інша відповідь.
3.2.64. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-1, 2-2, 3-3; б) 1-3, 2-2, 3-1; в) 1-2, 2-3, 3-1;
г) 1-2, 2-1, 3-3; д) інша відповідь.
3.2.65. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-3, 2-1, 3-2; б) 1-2, 2-3, 3-1; в) 1-1, 2-2, 3-3;
г) 1-2, 2-1, 3-3; д) інша відповідь.
3.2.66. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-2, 2-1, 3-3; б) 1-3, 2-2, 3-1; в) 1-1, 2-2, 3-3;
г) 1-3, 2-1, 3-2; д) інша відповідь.
3.2.67. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-3, 2-2, 3-1; б) 1-2, 2-1, 3-3; в) 1-1, 2-3, 3-2;
г) 1-1, 2-2, 3-3; д) інша відповідь.
3.2.68. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-1, 2-2, 3-3; б) 1-2, 2-1, 3-3; в) 1-3, 2-2, 3-1;
г) 1-2, 2-3, 3-1; д) інша відповідь.
3.2.69. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-2, 2-1, 3-3; б) 1-1, 2-2, 3-3; в) 1-1, 2-3, 3-2;
г) 1-3, 2-2, 3-1; д) інша відповідь.
3.2.70. Встановити відповідність:
1)![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-2, 2-3, 3-1; б) 1-1, 2-3, 3-2; в) 1-3, 2-1, 3-2;
г) 1-1, 2-2, 3-3; д) інша відповідь.
3.2.71. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-3, 2-1, 3-2; б) 1-2, 2-1, 3-3; в) 1-1, 2-3, 3-2;
г) 1-3, 2-2, 3-1; д) інша відповідь.
3.2.72. Встановити відповідність:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-1, 2-2, 3-3; б) 1-2, 2-1, 3-3; в) 1-2, 2-3, 3-1;
г) 1-3, 2-2, 3-1; д) інша відповідь.
3.2.73. Встановити відповідність між інтегралами:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-3, 2-2, 3-1; б) 1-1, 2-2, 3-3; в) 1-2, 2-3, 3-2;
г) 1-1, 2-3, 3-2; д) інша відповідь.
3.2.74. При раціоналізації
інтеграла
![]() встановити відповідність між підстановкою
і степенями
встановити відповідність між підстановкою
і степенями
![]() :
:
1)
![]() 1)
1)
![]() - ціле
- ціле
2)
![]() 2)
2)
![]() - ціле
- ціле
3)
![]() ,
де
,
де
![]() - найменший 3)
- найменший 3)
![]() - ціле
- ціле
спільний знаменник дробів
![]() ,
,![]()
а) 1-2, 2-1, 3-3; б) 1-3, 2-1, 3-2; в) 1-3, 2-2, 3-1;
г) 1-2, 2-3, 3-1; д) інша відповідь.
3.2.75. Встановити відповідність між інтегралами і підстановками:
1)
![]() 1)
1)
![]()
2)
![]() 2)
2)
![]()
3)
![]() 3)
3)
![]()
а) 1-3, 2-2, 3-1; б) 1-2, 2-3, 3-1; в) 1-1, 2-2, 3-3;
г) 1-3, 2-1, 3-2; д) інша відповідь.
3.2.76. Встановити відповідність між геометричними величинами та формулами для їх обчислення:
1) площа криволінійної трапеції
1)
![]()
2) об’єм тіла обертання навколо
осі
![]() 2)
2)
![]()
3) довжина дуги кривої
3)
![]()
а) 1-1, 2-3, 3-2; б) 1-3, 2-1, 3-2; в) 1-2, 2-3, 3-1;
г) 1-1, 2-2, 3-3; д) інша відповідь.
3.2.77. Встановити відповідність між інтегралами та методами інтегрування:
1)
![]() 1) підстановка
1) підстановка
![]()
2)
![]() 2) частинами
2) частинами
3)
![]() 3) підстановка
3) підстановка
![]()
а) 1-1, 2-2, 3-3; б) 1-3, 2-1, 3-2; в) 1-2, 2-1, 3-3;
г) 1-3, 2-2, 3-1; д) інша відповідь.
3.2.78. Площа криволінійної
трапеції, обмеженої кривою, заданою
параметрично
![]() ,
віссю
,
віссю
![]() і прямими
і прямими
![]() (
(![]() )
обчислюється за формулою:
)
обчислюється за формулою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.79. Площа криволінійного
сектора, обмеженого кривою, заданою в
полярних координатах функцією
![]() і двома променями
і двома променями
![]() ,
обчислюється за формулою:
,
обчислюється за формулою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.80. Довжина дуги кривої,
заданої параметрично
![]() обчислюється за фор-мулою:
обчислюється за фор-мулою:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.81. Довжина дуги, заданої в
полярних координатах рівнянням![]() обчислюється за формулою:
обчислюється за формулою:
а)
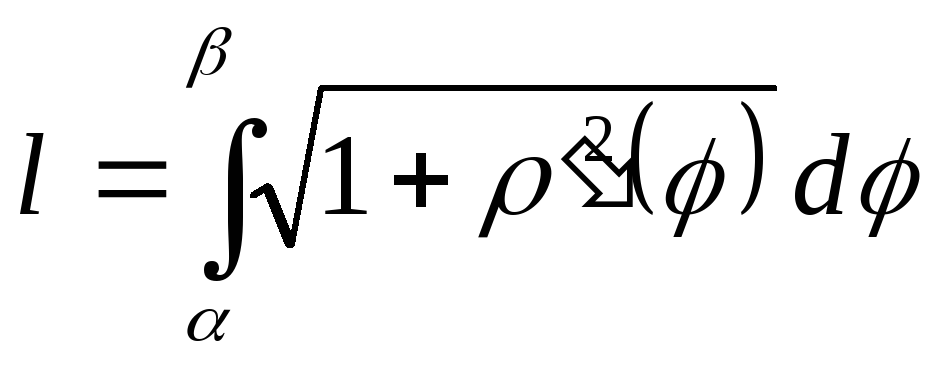 ;
б)
;
б)
![]() ;
;
в)
 ;
г)
;
г)
![]() ;
;
д) інша відповідь.
3.2.82. Площа
поверхні, утвореної обертанням кривої,
заданої рівнянням
![]() ,
,
![]() , навколо осі
, навколо осі
![]() ,
обчислюється за формулою:
,
обчислюється за формулою:
а)
![]() ;
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.83. Площа поверхні, утвореної
обертанням кривої, заданої параметрично
![]() ,
навколо осі
,
навколо осі
![]() ,
обчислюється за формулою:
,
обчислюється за формулою:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д) інша відповідь.
3.2.84. Інтеграл
![]() раціоналізується підстановкою:
раціоналізується підстановкою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
3.2.85. Інтеграл
![]() раціоналізується підстановкою:
раціоналізується підстановкою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д) інша відповідь.
;
д) інша відповідь.
