3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Таким образом, опытные данные не противоречат гипотезе о том, что содержание FeO в конечном шлаке подчиняется закону нормального распределения. Оцените самостоятельно моду, медиану, доверительный интервал для математического ожидания при вероятностях 90, 95 и 99,7%.

3.7. Преобразование распределений к нормальному

Если исследователь, использовав методы, изложенные в предыдущем параграфе, убедился, что гипотеза нормальности распределения не может быть принята, то вполне может быть, что с помощью существующих методов удастся так преобразовать исходные данные, что их распределение будет подчиняться нормальному закону распределения. Для пояснения идеи

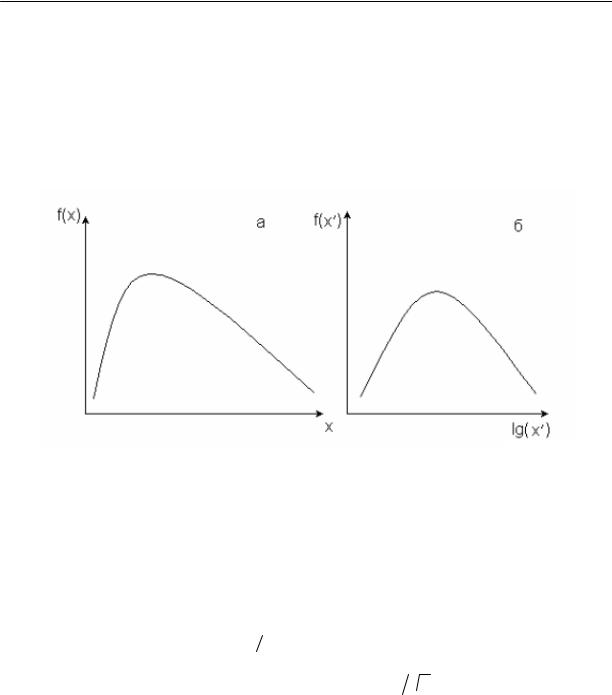
преобразований рассмотрим качественный пример. Пусть кривая

распределения f(x) имеет вид, представленный на рис. 3.9,а, т.е. имеются

очень крутая левая ветвь и пологая правая. Такое распределение отличается

от нормального.

Для выполнения операций преобразования каждое наблюдение

трансформируется с помощью логарифмического преобразования x′ = lg(x).

При этом левая ветвь кривой распределения сильно растягивается, и

распределение принимает приближенно нормальный вид (рис.3.9,б). Если при

114

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

преобразовании получаются значения, расположенные между 0 и 1, то все наблюдаемые значения для удобства расчетов и во избежание получения отрицательных параметров необходимо умножить на 10 в соответствующей степени, чтобы все вновь полученные, преобразованные значения были

больше единицы, т.е. необходимо выполнить преобразования x′′ = lg(x 10a ).

x′ = lg(x)

Рис. 3.9. Преобразование функции f(x) к нормальному распределению

Асимметричное распределение с одной вершиной приводится к нормальному преобразованием x′ = lg(x ±a). В отдельных случаях можно применять и другие преобразования:

а) обратная величина x′ =1 x;

б) обратное значение квадратных корней x′ =1 x.

Преобразование "обратная величина" является наиболее "сильным". Среднее положение между логарифмическим преобразованием и "обратной

величиной" занимает преобразование "обратное значение квадратных корней".

Для нормализации смещенного вправо распределения служат, например,

степенные преобразования x′ = xa . При этом для a принимают значения: а=1,5 при умеренном и а=2 при сильно выраженном правом смещении. Рекомендуем

читателю придумать такие преобразования, которые удовлетворяли бы исследователя в том или ином случае.

115

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Контрольные вопросы

1.Какие задачи решают в ходе предварительной статистической обработки экспериментальных данных?

2.Что такое генеральная совокупность и выборка?

3.Что такое точечное оценивание? Перечислите точечные оценки основных параметров нормального распределения для непрерывной случайной величины.

4.В чем заключается основная идея оценивания с помощью доверительного интервала? С помощью каких распределений происходит построение доверительных интервалов для математического ожидания и

дисперсии?

5.В чем заключается сущность статистических гипотез? Что такое нулевая и альтернативная статистические гипотезы?

6.С помощью каких критериев производится отсев грубых погрешностей?

7.Какие задачи возникают при сравнении двух рядов наблюдений экспериментальных данных? С помощью каких критериев они решаются?

8.Что такое критерий согласия? Какова основная идея его использования при проверке гипотез о виде функции распределения?

9.В чем заключается алгоритм использования критерия Пирсона для проверки гипотезы нормального распределения экспериментальных данных?

10.Какова процедура использования критерия Колмогорова-Смирнова для проверки гипотезы нормального распределения?

116

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

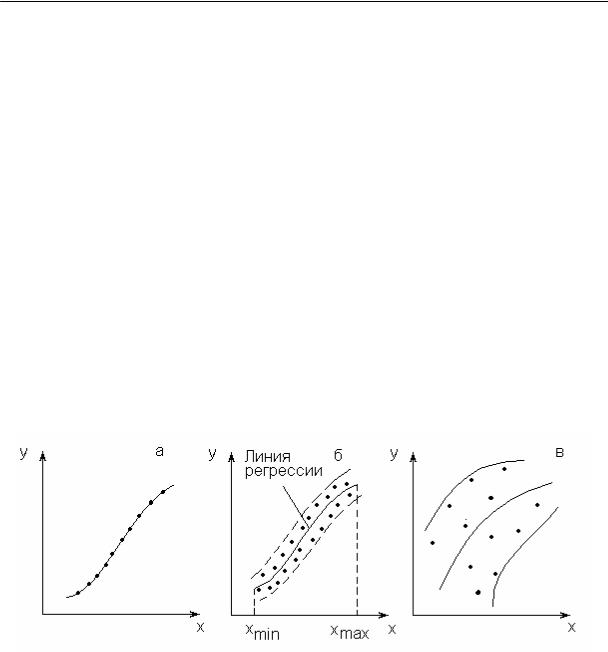
Функциональные связи (или зависимости) – это такие связи, когда при изменении величины X другая величина y изменяется так, что каждому значению xi соответствует совершенно определенное (однозначное) значение yi (рис.4.1,а). Таким образом, если выбрать все условия эксперимента абсолютно одинаковыми, то, повторяя испытания, получим одну и ту же зависимость, т.е. кривые идеально совпадут для всех испытаний.

К сожалению, такие условия в реальности не встречаются. На практике не удается поддерживать постоянство условий (например, физико-химические свойства шихты при моделировании процессов тепломассопереноса в металлургических печах). При этом влияние каждого случайного фактора в отдельности может быть мало, однако в совокупности они существенно могут повлиять на результаты эксперимента. В этом случае говорят о стохастической (вероят-

ностной) связи между переменными.

Рис.4.1. Виды связей: а – функциональная связь, все точки лежат на линии; б – связь достаточно тесная, точки

группируются возле линии регрессии, но не все они лежат

на ней; в – связь слабая

Стохастичность связи состоит в том, что одна случайная переменная y

реагирует на изменение другой X изменением своего закона распределения

(см. рис. 4.1, б). Таким образом, зависимая переменная принимает не одно кон-

кретное значение, а некоторое из множества значений. Повторяя испытания, мы будем получать другие значения функции отклика, и одному и тому же значению X в различных реализациях будут соответствовать различные значения

118

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

y в интервале [xmin; xmax]. Искомая зависимость y) =f(X) может быть найдена лишь в результате совместной обработки полученных значений X и y.

На рис. 4.1, б – это кривая зависимости, проходящая по центру полосы экспериментальных точек (математическому ожиданию), которые могут и не лежать на искомой кривой y =f(X), а занимают некоторую полосу вокруг нее.

Эти отклонения вызваны погрешностями измерений, неполнотой модели и учитываемых факторов, случайным характером самих исследуемых процессов и другими причинами.

Анализ стохастических связей приводит к различным постановкам задач статистического исследования зависимостей, которые упрощенно можно классифицировать следующим образом:

1)задачи корреляционного анализа – задачи исследования наличия взаимосвязей между отдельными группами переменных ;

2)задачи регрессионного анализа – задачи, связанные с установлением аналитических зависимостей между переменным y и одним или несколькими переменными x1, x2, ..., xi, ..., xk, которые носят количественный характер;

3)задачи дисперсионного анализа – задачи, в которых переменные x1, x2, ..., xi,

Стохастические зависимости характеризуются формой, теснотой связи и численными значениями коэффициентов уравнения регрессии.

Форма связи устанавливает вид функциональной зависимости y)=f(X) и

характеризуется уравнением регрессии. Если уравнение связи линейное, то имеем линейную многомерную регрессию, в этом случае зависимость y от X

описывается линейной зависимостью в k-мерном пространстве:

j=1

где b0, ..., bj, ..., bk – коэффициенты уравнения. Для пояснения существа используемых методов ограничимся сначала случаем, когда x – скаляр. В общем

119

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

случае виды функциональных зависимостей в технике достаточно многообраз-

ны: показательные y = b0x b1 , логарифмические y = b0 lg(x) и т.д.

Заметим, что задача выбора вида функциональной зависимости – задача неформализуемая, так как одна и та же кривая на данном участке примерно с одинаковой точностью может быть описана самыми различными аналитическими выражениями. Отсюда следует важный практический вывод. Даже в наш век компьютеров принятие решения о выборе той или иной математической модели остается за исследователем. Только экспериментатор знает, для чего будет в дальнейшем использоваться эта модель, на основе каких понятий будут интерпретироваться ее параметры.

Крайне желательно при обработке результатов эксперимента вид функ-

ции y =f(X) выбирать, исходя из условия ее соответствия физической природе изучаемых явлений или имеющимся представлениям об особенностях поведения исследуемой величины. К сожалению, такая возможность не всегда имеется, так как эксперименты чаще всего проводятся для исследования недостаточно или неполно изученных явлений.

120