Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тюменский Государственный Нефтегазовый Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

решение различных Задач в мат каде

.pdf

Скачиваний:

Добавлен:

17.02.2016

Размер:

529.78 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

2. Решить дифференциальное уравнение y’=f(x,y) методом Рунге-Кутта на отрезке [a,b] с шагом h c начальным условием y(a)=y0.

Таблица 5

N		Функция		a	b	y0	h

1			3x − y	2	3	1	0.1
			x2 + y

2	2x + y + 4			3	4	1	0.1
			2y + x

3			x2 − y	0	1	2	0.1
		2x + y +1

4		x2 − y + 2		2	3	1	0.1
			xy +3x

				32

5		3 − x − y2		1	2	1	0.1
			2 − xy2

6	2 − x − y 2 x			0	1	1	0.1
			3x + y

7			1+3xy	0	1	2	0.1
		5 − x + y 2

8			x2 y + 2	0	1	1	0.1
			2x − y

9		x2 + y + 2		2	3	2	0.1
			2x − y

10			xy + 4	0	1	3	0.1
	2 y − xy +1

			КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Проверить для дифференциального уравнения условия теоремы существования и единственности.

2.На какие основные группы подразделяются приближенные методы решения дифференциальных уравнений?

3.В какой форме можно получить решение дифференциального уравнения по методу Эйлера?

4.Каков геометрический смысл решения дифференциального уравнения методом Эйлера?

5.В какой форме можно получить решение дифференциального уравнения по методу Рунге-Кутта?

6.Какой способ оценки точности используется при приближенном интегрировании дифференциальных уравнений методами Эйлера и РунгеКутта?

7.Как вычислить погрешность по заданной формуле, используя метод двойного пересчета?

Лабораторная работа №6 ТЕМА: СТАТИСТИЧЕСКАЯ ОБРАБОТКА ОПЫТНЫХ

ДАННЫХ

Пусть зависимость между переменными x и y задана таблично

(заданы опытные данные). Требуется найти функцию в некотором смысле наилучшим образом описывающую данные. Одним из способов подбора такой (приближающей) функции является метод наименьших квадратов.

Метод состоит в том, чтобы сумма квадратов отклонений значений искомой функции yi = y(xi ) и заданной таблично yi была наименьшей:

S(c) =( y − y )2

+ ( y

− y

+K+ ( y

− y

)2 → min

(6.1)

где c − вектор параметров искомой функции.

Задание 1

Построить методом наименьших квадратов две эмпирические

формулы: линейную и квадратичную.

В случае линейной функции

y = ax +b

задача сводится нахождению

параметров a и b из системы линейных уравнений

M x

2 a + M xb = M xy

, где

a + b = M

M x 2

∑xi 2 ,

M x

∑xi ,

M xy =

∑xi yi , My=

∑yi

n i =1

i=1

а в случае квадратичной зависимости

y = ax2 + bx + c к

нахождению

параметров a , b и c из системы уравнений:

M x4 a + M x3 b + M x2 c = M x2 y

3 a + M

2 b + M xc = M xy

, где

2 a + M

b +c = M

∑xi 4 , M =

∑xi

3 , M

∑xi 2 yi

n i =1

Выбрать из двух функций наиболее подходящую. Для этого составить таблицу для подсчета суммы квадратов уклонений по формуле (6.1). Исходные данные взять из таблицы 6.

Задание 2

Составить программу для нахождения приближающих функций заданного типа с выводом значений их параметров и соответствующих им сумм квадратов уклонений. Выбрать в качестве приближающих функций следующие: y = ax +b , y = axm , y = aemx . Провести линеаризацию.

Определить для какого вида функции сумма квадратов уклонений является наименьшей.

Исходные данные помещены в таблице 6.

Примерный фрагмент выполнения лабораторной работы

i 1.. 10

x1 0.5

x2 0.1

x3 0.4

x4 0.2

x5 0.6

x6 0.3

x7 0.4

x8 0.7

x9 0.3

x10 0.8

mx2 1

y1		1.8


y2		1.1


y3		1.8


y4		1.4


y5		2.1


y6		1.8


y7		1.6


y8		2.2


y9		1.5


y10	2.3

	10
	x	2
	i
	i = 1	mx 1.
	10	mx 1.
	10

10			10				10
	x		x	.y	i		y	i
	i		i		i			i
i = 1	mxy	1	i = 1			my 1	i = 1
10	mxy	1	10			my 1	10
10			10				10

mx2= 0.229

mx= 0.43

mxy = 0.828

my = 1.76

given

mx2a. mx.b mxy mx.a b my

find( a,b )

1.6145124716553287982

1.0657596371882086168

											Таблица 6
i		1	2	3	4	5	6	7	8	9	10
№
1	x	0.5	0.1	0.4	0.2	0.6	0.3	0.4	0.7	0.3	0.8
						35


	y	1.8	1.1	1.8	1.4	2.1	1.8	1.6	2.2	1.5	2.3

2	x	1.7	1.5	3.7	1.1	6.2	0.3	6.5	3.6	3.8	5.9

	y	1.5	1.4	1.6	1.3	2.1	1.1	2.2	1.8	1.7	2.3

3	x	1.7	1.1	1.6	1.2	1.9	1.5	1.8	1.4	1.3	1.0

	y	6.7	5.6	6.7	6.1	7.4	6.9	7.9	5.9	5.6	5.3

4	x	1.3	1.2	1.5	1.4	1.9	1.1	2.0	1.6	1.7	1.8

	y	5.5	5.9	6.3	5.8	7.4	5.4	7.6	6.9	6.6	7.5

5	x	2.3	1.4	1.0	1.9	1.5	1.8	2.1	1.6	1.7	1.3

	y	5.3	3.9	2.9	5.0	4.0	4.9	5.1	4.5	4.1	3.7

6	x	1.8	2.6	2.3	1.3	2.0	2.1	1.1	1.9	1.6	1.5

	y	4.4	6.4	5.3	3.7	4.9	5.6	3.0	5.0	4.3	3.7

7	x	1.9	2.1	2.0	2.9	3.0	2.6	2.5	2.7	2.2	2.8

	y	6.6	7.6	6.7	9.2	9.4	7.8	8.4	8.0	7.9	8.7

8	x	2.0	1.4	1.0	1.7	1.3	1.6	1.9	1.5	1.2	2.1

	y	7.5	6.1	4.8	7.4	5.7	7.0	7.1	6.8	6.0	8.9

9	x	2.0	1.2	1.8	1.9	1.1	1.7	1.6	1.4	1.5	1.3

	y	7.5	5.9	7.0	8.0	5.0	7.4	6.4	6.6	6.3	5.7

10	x	1.9	1.1	1.4	2.3	1.7	2.1	1.6	1.5	1.0	1.2

	y	4.7	3.4	3.8	5.2	4.6	5.5	3.9	3.9	3.2	3.5

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.В чем суть приближения таблично заданной функции по методу наименьших квадратов?

2.Чем отличается этот метод от метода интерполяции?

3.Каким образом сводится задача построения приближающих функций в виде различных элементарных функций к случаю линейной функции?

4.Может ли сумма квадратов уклонений для каких-либо приближающих функций быть равной нулю?

5.Какие элементарные функции используются в качестве приближающих функций?

6.Как найти параметры для линейной и квадратичной зависимости, используя метод наименьших квадратов?

Лабораторная работа №7

Тема : Численное решение уравнений в частных производных

Рассмотрим смешанную задачу для уравнения теплопроводности, а именно, найти функцию u(x, t) , удовлетворяющую уравнению

∂u	−	∂2u	= 0		(7.1)
∂t		∂x2

начальному условию
u(x,0) = f (x),				x (0, s) ,	(7.2)
и краевым условиям
u(0,t) =ϕ(t),				u(l,t) =ψ(t) , t (0,T ) .	(7.3)

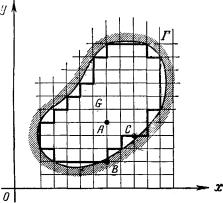
Задачу будем решать методом сеток (конечных разностей). В основе метода лежит идея замены производных конечно-разностными отношениями. Ограничимся случаем двух независимых переменных. Пусть в плоскости хОу имеется некоторая область G с границей Г (рис. 1).

Рис 1

Построим на плоскости два семейства параллельных прямых: x =ih , t = kl , i=0,1,2,…, k=0,1,2,…

Точки пересечения этих прямых назовем узлами. Два узла называются соседними, если они удалены друг от друга в направлении оси Ох или Оу на расстояние, равное шагу сетки h или l соответственно. Выделим узлы, принадлежащие области G+Г, а также некоторые узлы, не принадлежащие этой области, но расположенные на расстоянии, меньшем чем шаг, от границы Г. Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними (узел А, рис. 1). Оставшиеся из выделенных узлов называются граничными (узлы В, С). Обозначим xi =ih, y j = kl.

Значения искомой функции и=и(х,у) в узлах сетки будем обозначать

через

ui,k =u(ih,kl). В

каждом внутреннем узле (ih,kl) заменим частные

производные разностными отношениями:

(

)ik

≈

ui+1,k −ui−1,k

(

)ik

≈

ui,k +1 −ui,k −1

В граничных точках воспользуемся формулами вида

(

)ik

≈

ui+1,k −ui,k

(

)ik ≈

ui,k +1 −ui,k

Аналогично заменяются частные производные второго порядка

(

d 2u

)ik

≈

ui,k +1 − 2uik + ui,k −1

dx2

l 2

d 2u

Сделаем

переход

от

уравнения вида

−

= 0

к разностному

уравнению

ui,k +1

− ui,k

ui+1,k

− 2uik + ui−1,k

=0.

После

замены σ =

преобразований

получаем

уравнение для

вычисления внутренних узлов

ui,k +1 =(1 − 2σ)uik

+σ(ui+1,k

ui−1,k )

(7.4)

При 0 ≤σ ≤1/ 2 разностное уравнение (7.4) устойчиво [7]. Наиболее простой вид уравнение имеет при σ =1/ 2. В этом случае уравнение (7.2) запишется в виде

uik +1	=	ui−1k + ui+1k					(7.5)

	2
Пусть				(x,t) – точное решение задачи (7.1)-(7.3),		− u		– отклонение
			u		u

точного значения от вычисленного по методу сеток. Тогда погрешность вычислений может быть вычислена по формуле

	− u	≤ T m h2		,	(7.6)

u

		3	1

где m1= max{| f (4) (x) |, |ϕ′′(t) |, |ψ′′(t) |}, где 0 ≤t ≤T , 0 ≤ x ≤ s.

Задание 1

Используя метод сеток, найти приближенное решение уравнения (7.1)- (7.3), удовлетворяющее условиям u(x,0) = f (x), u(x0 ,t) = 0, u(xn ,t) = 0 , для

0 ≤t ≤ 0.03, x0 ≤ x ≤ xn и h=0.1, l=0.005.

Решение должно быть оформлено в виде таблицы 7.1 подсчитанной вручную. Исходные данные заданы в таблице 7.2. Оценить погрешность вычислений по формуле (7.6).

Комментарий. Значения ui0 находим, подставляя значение хо в	f (x) .
Например, f (x0 ) = x0 sin(2πx0 ) при x0 = 0 равна 0. Значения u0k	и u5k

определяются краевыми условиями (в нашем случае нулевые). Далее

значение, например, u

находим, используя формулу (7.5), т.е. u

u00 + u20

и т.д.

Таблица 7.1.

x0 + h

x0 + 2h

x 0 + 3 h

x0 + 4h

u00

u10

u20

u30

u40

u50

0.005

u01

u11

u31

u41

u51

0.010

u02

u12

u22

u32

u42

u52

0.015

u03

u13

u23

u33

u43

u53

0.020

u04

u14

u24

u34

u44

u54

0.025

u05

u15

u25

u35

u45

u55

0.03

u06

u16

u26

u36

u46

u56

			Таблица 7.2
№ варианта	x0	xn	f (x)
1	0.1	0.6	(1.1x2 +1.1)sin(2π(x − 0.1))

2	0	0.5	xsin(2πx)

3	0.2	0.7	(1.5x +1.1)sin(2π(x − 0.2))

4	0	0.5	(x2 + 3)sin(2πx)

5	0.1	0.6	(1.1x2 −1.3)sin(2π(x − 0.1))

6	0.2	0.7	(x3 +1)sin(2π(x − 0.2))

7	0	0.5	(1.5x2 +1)sin(2πx)

8	0.2	0.7	(3x2 + 2)sin(2π(x − 0.2))

				9																			0						0.5									(x2			−1.3)sin(2πx)

				10													0.1												0.6							(3x2 −1)sin(2π(x − 0.1))

					Примерный фрагмент																									выполнения лабораторной работы
f( x)		x.cos		( 2				3 .x)								i						0 .. 5				j		0 .. 4
		x0				0.1								x5					0.6


							xi				x0					x0							x5
																x0							x5
																	6


u i ,0		f xi							u 0 ,j						1					0					u 5 ,j		1			0


									i				1 .. 4
									i				1 .. 4
		u i ,1						u i				1 ,0						u i					1 ,0								u	i	1	,1		u	i		1 ,1
		u i ,1																													u					u
														2															u i ,2

																																			2
																																			2
		u i ,3						u i				1 ,2						u i					1 ,2

														2																						u i						u i
														2
																															u i ,4							1 ,3					1 ,3

																																								2
																																								2
			u i ,5						u i					1 ,4							u i			1 ,4
			u i ,5														2
																	2
				0.191						0							0								0				0			0
				0.191						0							0								0				0			0
				0.352						0.271							0.176								0.156				0.132			0.1
	u =			0.352						0.352							0.311								0.264				0.2		0.176
	u =			0.352						0.352							0.352								0.244				0.22		0.161
				0.352						0.352							0.176								0.176				0.122		0.11
				0.352						0							0								0				0			0

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.В чем суть метода сеток?

2.Какие точки называются узлами?

3.Что такое шаг сетки?

4.Какие узлы называются внутренними и какие граничными?

5.Как перейти от дифференциального уравнения к разностному (на примере уравнения теплопроводности)?

6.Какое уравнение используется для вычисление текущего слоя?

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.02.201629.06 Кб16Реферат по ТО.docx
#
09.09.2019128.51 Кб9Реферат правильно.doc
#
17.02.201629.19 Кб57Реферат физ-ра.docx
#
26.09.201981.41 Кб2реферат ЭБ.doc
#
17.02.2016230.44 Кб97Реферат.docx
#
17.02.2016529.78 Кб35решение различных Задач в мат каде.pdf
#
19.07.2019164.86 Кб3Рихтовка .doc
#
17.02.2016578.79 Кб144РКС.docx
#
30.07.2019582.03 Кб20Роль и место геофизических исследований скважин....docx
#
17.02.20161.55 Mб27РП.Формирование кадастровых дел.doc
#
17.02.201617.5 Mб46Рубцова.djvu


	y	1.8	1.1	1.8	1.4	2.1	1.8	1.6	2.2	1.5	2.3

2	x	1.7	1.5	3.7	1.1	6.2	0.3	6.5	3.6	3.8	5.9

	y	1.5	1.4	1.6	1.3	2.1	1.1	2.2	1.8	1.7	2.3

3	x	1.7	1.1	1.6	1.2	1.9	1.5	1.8	1.4	1.3	1.0

	y	6.7	5.6	6.7	6.1	7.4	6.9	7.9	5.9	5.6	5.3

4	x	1.3	1.2	1.5	1.4	1.9	1.1	2.0	1.6	1.7	1.8

	y	5.5	5.9	6.3	5.8	7.4	5.4	7.6	6.9	6.6	7.5

5	x	2.3	1.4	1.0	1.9	1.5	1.8	2.1	1.6	1.7	1.3

	y	5.3	3.9	2.9	5.0	4.0	4.9	5.1	4.5	4.1	3.7

6	x	1.8	2.6	2.3	1.3	2.0	2.1	1.1	1.9	1.6	1.5

	y	4.4	6.4	5.3	3.7	4.9	5.6	3.0	5.0	4.3	3.7

7	x	1.9	2.1	2.0	2.9	3.0	2.6	2.5	2.7	2.2	2.8

	y	6.6	7.6	6.7	9.2	9.4	7.8	8.4	8.0	7.9	8.7

8	x	2.0	1.4	1.0	1.7	1.3	1.6	1.9	1.5	1.2	2.1

	y	7.5	6.1	4.8	7.4	5.7	7.0	7.1	6.8	6.0	8.9

9	x	2.0	1.2	1.8	1.9	1.1	1.7	1.6	1.4	1.5	1.3

	y	7.5	5.9	7.0	8.0	5.0	7.4	6.4	6.6	6.3	5.7

10	x	1.9	1.1	1.4	2.3	1.7	2.1	1.6	1.5	1.0	1.2

	y	4.7	3.4	3.8	5.2	4.6	5.5	3.9	3.9	3.2	3.5


	y	1.8	1.1	1.8	1.4	2.1	1.8	1.6	2.2	1.5	2.3

2	x	1.7	1.5	3.7	1.1	6.2	0.3	6.5	3.6	3.8	5.9

	y	1.5	1.4	1.6	1.3	2.1	1.1	2.2	1.8	1.7	2.3

3	x	1.7	1.1	1.6	1.2	1.9	1.5	1.8	1.4	1.3	1.0

	y	6.7	5.6	6.7	6.1	7.4	6.9	7.9	5.9	5.6	5.3

4	x	1.3	1.2	1.5	1.4	1.9	1.1	2.0	1.6	1.7	1.8

	y	5.5	5.9	6.3	5.8	7.4	5.4	7.6	6.9	6.6	7.5

5	x	2.3	1.4	1.0	1.9	1.5	1.8	2.1	1.6	1.7	1.3

	y	5.3	3.9	2.9	5.0	4.0	4.9	5.1	4.5	4.1	3.7

6	x	1.8	2.6	2.3	1.3	2.0	2.1	1.1	1.9	1.6	1.5

	y	4.4	6.4	5.3	3.7	4.9	5.6	3.0	5.0	4.3	3.7

7	x	1.9	2.1	2.0	2.9	3.0	2.6	2.5	2.7	2.2	2.8

	y	6.6	7.6	6.7	9.2	9.4	7.8	8.4	8.0	7.9	8.7

8	x	2.0	1.4	1.0	1.7	1.3	1.6	1.9	1.5	1.2	2.1

	y	7.5	6.1	4.8	7.4	5.7	7.0	7.1	6.8	6.0	8.9

9	x	2.0	1.2	1.8	1.9	1.1	1.7	1.6	1.4	1.5	1.3

	y	7.5	5.9	7.0	8.0	5.0	7.4	6.4	6.6	6.3	5.7

10	x	1.9	1.1	1.4	2.3	1.7	2.1	1.6	1.5	1.0	1.2

	y	4.7	3.4	3.8	5.2	4.6	5.5	3.9	3.9	3.2	3.5


	y	1.8	1.1	1.8	1.4	2.1	1.8	1.6	2.2	1.5	2.3

2	x	1.7	1.5	3.7	1.1	6.2	0.3	6.5	3.6	3.8	5.9

	y	1.5	1.4	1.6	1.3	2.1	1.1	2.2	1.8	1.7	2.3

3	x	1.7	1.1	1.6	1.2	1.9	1.5	1.8	1.4	1.3	1.0

	y	6.7	5.6	6.7	6.1	7.4	6.9	7.9	5.9	5.6	5.3

4	x	1.3	1.2	1.5	1.4	1.9	1.1	2.0	1.6	1.7	1.8

	y	5.5	5.9	6.3	5.8	7.4	5.4	7.6	6.9	6.6	7.5

5	x	2.3	1.4	1.0	1.9	1.5	1.8	2.1	1.6	1.7	1.3

	y	5.3	3.9	2.9	5.0	4.0	4.9	5.1	4.5	4.1	3.7

6	x	1.8	2.6	2.3	1.3	2.0	2.1	1.1	1.9	1.6	1.5

	y	4.4	6.4	5.3	3.7	4.9	5.6	3.0	5.0	4.3	3.7

7	x	1.9	2.1	2.0	2.9	3.0	2.6	2.5	2.7	2.2	2.8

	y	6.6	7.6	6.7	9.2	9.4	7.8	8.4	8.0	7.9	8.7

8	x	2.0	1.4	1.0	1.7	1.3	1.6	1.9	1.5	1.2	2.1

	y	7.5	6.1	4.8	7.4	5.7	7.0	7.1	6.8	6.0	8.9

9	x	2.0	1.2	1.8	1.9	1.1	1.7	1.6	1.4	1.5	1.3

	y	7.5	5.9	7.0	8.0	5.0	7.4	6.4	6.6	6.3	5.7

10	x	1.9	1.1	1.4	2.3	1.7	2.1	1.6	1.5	1.0	1.2

	y	4.7	3.4	3.8	5.2	4.6	5.5	3.9	3.9	3.2	3.5