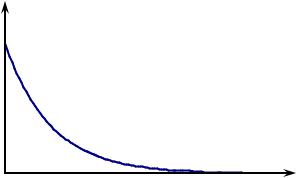
Зависимость зарядного тока от времени имеет вид:
i = |
−U + ε |
= |
|
ε |
e |
− |
t |
|
|||
|
RC . |
||||||||||
R |
|
R |
|
||||||||
Сила тока имеет наибольшее значение в начальный момент |
|||||||||||
времени и асимптотически стремится к нулю в процессе зарядки. |
|||||||||||
Рассмотрим процесс разряда конденсатора. Исходные уравнения в |
|||||||||||
этом случае будут иметь вид: |
|
q |
, i = − dq . |
||||||||
iR = U , U = |
|||||||||||
C |
|||||||||||
|
|
|
|
|
|
|
dt |
||||
В выражение для силы |
тока i |
|
|
входит знак минус, так как |
|||||||
выбранное нами положительное направление тока соответствует уменьшению заряда конденсатора. Исключая из записанных равенств q и
i , получим:
dU + |
1 |
U = 0 , |
|
||||
|
|
||||||
dt |
RC |
|
|||||
откуда |
|
|
|
t |
|
||
U = Be− |
|
||||||
|
|
. |
|
||||
RC |
|
||||||
Если начало отсчета времени совпадает с началом процесса |
|||||||
разрядки, то начальное условие будет: |
|
|
|
|
|
|
|
t = 0, U = ε . |
|
||||||
В этом случае постоянная |
интегрирования равна B = ε |
и |
|||||
зависимость напряжения конденсатора от времени имеет вид (рис. 3): |
|
||||||
U = ε e− |
t |
|
|||||
|
. |
(10) |
|||||
RC |
|||||||
Полученные результаты показывают, что процессы зарядки и разрядки (установление электрического равновесия) происходят не мгновенно, а с конечной быстротой. Для рассмотренного контура,
содержащего сопротивление и емкость, быстрота установления зависит от
произведения
U |
|
ε |
|
Рис. 3 |
t |
|
τ = RC ,
которое имеет размерность времени и называется постоянной времени данного контура или
временем релаксации (от лат. relaxаtio - ослабление). Постоянная времени показывает, через какое
время после |
выключения |
ЭДС |
напряжение |
уменьшается |
в |
e = 2,71 раза. |
|
|
18
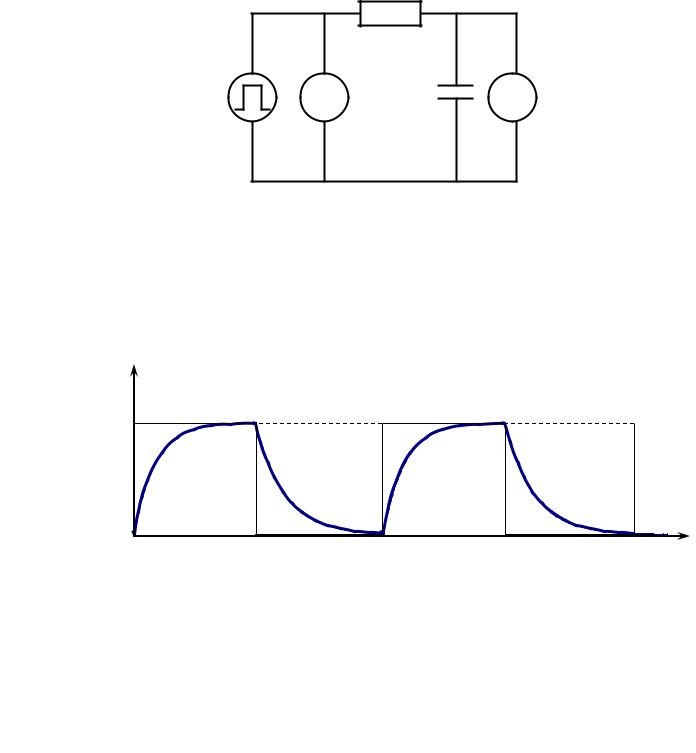
Описание экспериментальной установки
Принципиальная электрическая схема для наблюдения процессов заряда и разряда конденсатора изображена на рис. 4.
С генератора сигналов специальной формы прямоугольные импульсы через сопротивление R поступают на конденсатор C . В момент времени t1 (рис. 5) конденсатор начинает заряжаться через сопротивление
R , напряжение на конденсаторе увеличивается от нуля до ε по экспоненциальному закону согласно выражению (9). В момент времени t2
(рис. 5) импульс заканчивается, напряжение на входе схемы равно нулю, и конденсатор начинает разряжаться через сопротивление R . Напряжение на
обкладках конденсатора уменьшается по экспоненциальному закону согласно выражению (10).
R
C
V0 |
V1 |
Рис. 4
На рис. 5 приведена зависимость напряжения на обкладках
конденсатора для различных моментов времени при его зарядке и разрядке. В момент времени t3 от генератора напряжений поступает новый
импульс и процессы заряда и разряда повторяются. Кривые заряда и
разряда конденсатора можно наблюдать на экране электронного осциллографа.
U |
|
|
|
ε |
|
|
|
t1 |
t2 |
t3 |
t |
|
|
Рис. 5 |
|
19
Порядок выполнения эксперимента
1.Подсоедините к гнездам V0 коннектора регулируемый источник
напряжений специальной формы настроенный на прямоугольные импульсы положительной полярности. Ручкой «частота» установите частоту импульсов f =250 Гц. Ручку «амплитуда» выведите в крайнее правое положение. Предел вольтметра V0 установите 20В.
2.Приведите компьютер в рабочее состояние, «включите» виртуальный осциллограф и настройте его так, чтобы на экране было изображение прямоугольных импульсов.
3.Соберите на наборном поле цепь согласно схеме (рис. 4). Значения
емкости C и сопротивления R возьмите по указанию преподавателя
(C =1 мкФ R =1 кОм, C =0,47 мкФ R =1 кОм, C =1 мкФ R =470 Ом).
Измерительные приборы V0 и V1, в схеме – это соответствующие пары гнезд коннектора.
4.Перерисуйте осциллограмму напряжения на бумагу с масштабной координатной сеткой, или сделайте печатную копию экрана.
5.Изменяя частоту прямоугольных импульсов от 250 Гц до 600 Гц
|
через 50 Гц зарисовать осциллограммы напряжений. |
|
|
|
|||||||||
6. |
Отключите |
вольтметр |
V0. Вернув |
ручку «частота» |
в положение |
||||||||
|
f =250 Гц и меняя частоту развертки, добейтесь, чтобы на экране |
||||||||||||
|
осциллографа осталась только одна кривая разряда. Нажмите кнопку |
||||||||||||
|
«записать в файл» и сохраните файл в папке. |
|
|
|
|||||||||
7. |
Занесите полученные значения в таблицу. |
|
|
|
|||||||||
|
t , мс |
|
|
|
|
|
|
|
|
|
|
|
|
|
U , В |
|
|
|
|
|
|
|
|
|
|
|
|
8. |
lnU |
|
|
|
|
|
|
|
|
|
|
|
|
Постройте |
графики |
зависимостей U = f (t) и lnU = f (t). |
|||||||||||
9. |
Определите время релаксации разряда по формуле τ = |
t |
|||||||||||
(lnU ) |
|
||||||||||||
10.Рассчитайте |
время |
релаксации |
(τ = RC ) по |
номинальным |
|||||||||
параметрам R и C , указанным на миниблоках, и сравните её с экспериментальным значением.
Контрольные вопросы.
1.Что называется конденсатором? Дайте определение емкости конденсатора.
2.Запишите выражение для емкости плоского конденсатора.
3.Получите законы изменения напряжения на конденсаторе в процессе его заряда и разряда.
4.Что называется временем релаксации цепи?
20
ЛАБОРАТОРНАЯ РАБОТА № 4
ИССЛЕДОВАНИЕ СЕГНЕТОЭЛЕКТРИКА
Цель работы: ознакомление со свойствами сегнетоэлектриков,
осциллографическим методом получения кривой поляризации и её зависимости от температуры.
Краткое теоретическое введение
Диэлектриками называются вещества, в которых микроскопические заряды связаны друг с другом.
При внесении диэлектрика во внешнее поле напряженностью E0
происходит смещение связанных зарядов: положительных - по полю; отрицательных - против поля.
В результате этого смещения в диэлектрике возникает собственное макроскопическое электрическое поле напряженностью E/ , направленное против внешнего поля: E/ -¯ E0 . Суммарное поле в диэлектрике определится как суперпозиция этих полей:
E = E0 + E/ .
Это явление называется поляризацией диэлектрика.
Количественной характеристикой поляризации диэлектрика является векторная величина P , называемая поляризованностью. Ее физический смысл заключается в следующем: поляризованность численно равна дипольному моменту единицы объема вещества.
Примечание. Диполем называется система из двух равных по величине и противоположных по знаку электрических зарядов -q и +q, расположенных на некотором расстоянии l друг
l |
от друга. Вектор l |
называется плечом диполя, |
||
-q |
+q вектор |
r |
×l |
называется дипольным |
p = q |
||||
|
моментом. |
|
|
|
Поляризованность диэлектрика P |
|
равна векторной сумме |
||
дипольных моментов всех молекул, содержащихся в единице объема
вещества: |
r |
|
|
||
r |
å pi |
|
P = |
V |
. |
|
||
|
V |
|
Опытным путем установлено, |
что в однородных изотропных |
|
диэлектриках поляризованность пропорциональна напряженности поля: P E и можно записать:
P = χε0 E |
(1) |
21