Sootvetstvija_funkcii_otnoshenija_lekcii

1.3.Соответствия

Изучая окружающий нас мир, математика рассматривает не только его объекты, но и главным образом связи между ними. Эти связи называют зависимостями, соответствиями, отношениями, функциями. Например, при вычислении длин предметов устанавливаются соответствия между предметами и числами, которые являются значениями их длин; при решении задач на движение устанавливается зависимость между пройденным путем и временем, если скорость движения известна.

Конкретные зависимости, соответствия, отношения между объектами в математике изучались с момента ее возникновения. Но вопрос о том, что общее имеют самые разные соответствия, какова сущность любого соответствия, был поставлен в конце - начале века, и ответ на него был найден в рамках теории множеств.

Итак, соответствие – способ задания взаимосвязей, взаимодействий между элементами множества (наряду с отношениями). Частными случаями соответствий являются функции, отображения, преобразования, операции и др.

Рассмотрим два множества А и В. Элементы этих множеств могут каким-то образом сопоставляться друг другу, образуя пары (a,b), а А, b В. Если закон, по которому элементу а А сопоставляется элемент b В, задан, то говорят, что между множествами А и В установлено соответствие

G.

Соответствием между множествами А и В называется подмножество G прямого произведения этих множеств: G A B.

При этом в соответствии не обязательно участвуют все элементы множества А и все элементы множества В.

Если (a,b) G, то говорят, что элемент b сопоставляется элементу а при соответствии G.

Чтобы задать соответствие, необходимо определить:

1)множество А – множество элементов, которым сопоставляются элементы множества В (множество отправлений соответствия);

2)множество В – множества элементов, которые сопоставляются элементам множества А (множество назначений соответствия);

3)G А В – определяет закон, по которому элементам А сопоставляются элементы В (график соответствия).

Таким образом, каждое соответствие задается тройкой g=(A,B,G),

при этом Пр1G A называется областью определения соответствия; Пр2G B - областью значений соответствия (см. рис. 1.12).

Если Пр2G=B, то G называется сюръективным.

1

Пусть соотношение G задает соответствие между множеством вещественных чисел R (осью абсцисс) и множеством R (осью ординат), т.е. G R R. Графически это соответствие представляет собой прямую линию (рис. 1.13 а)). Тогда соответствие G является:

всюду определенным, т.к. Пр1G=R;

сюръективно, т.к. Пр2 G = R;

функционально, т.к. любому x R из области определения

соответствует единственный элемент y из области значений;

взаимно однозначно, т.к. любому y из области значений соответствует единственный элемент x из области определения.

2) Пусть G – множество всех пар действительных чисел (x,y), удовлетворяющих соотношению x2 + y2 4. Графически это соответствие представляет собой круг радиуса 2 с центром в точке (0,0) (рис.1.13 б)). Таким образом круг G задает соответствие между R и R , т.е. G R R.

Это соответствие является частично определенным, т.к. Пр1G=[-1,1]R; не сюръективным, т.к. Пр2G=[-1,1] R; не функциональным.

Если А = [-1;1], B = [-1;1], т.е. G [-1,1] [-1,1], то соответствие G сюръективное, всюду определенное, но не функциональное.

3)Англо-русский словарь устанавливает соответствие между множествами английских и русских слов. Это соответствие не является функциональным, т.к. одному английскому слову , как правило, соответствует несколько русских слов. Кроме того, это соответствие является частично определенным, т.к. всегда можно найти английское слово, которого нет в данном словаре. Аналогично устанавливается, что это соответствие не является сюръективным.

4)Пусть даны множества А={1,2}, B={3,4}, тогда A B={(1,3), (1,4),(2,3),(2,4)}. Соответствие G является подмножеством прямого произ-

ведения А В. Т.к. существует 2n подмножеств множества А В, значит существует 2n=24=16 возможных соответствий между А и В. Например, некоторые из них:

G1={(1,3)}, Пр1G1={1} A, Пр2G1={3} B;

G2={(1,3),(2,3}, Пр1G1={1,2}=A, Пр2G1={3} B.

Для каждого соответствия g=(A,B,G), G A B существует обратное соответствие, которое элементам y множества В ставит в соответствие элементы x множества А, т.е. g-1=(B,A,G-1), где G-1 B A.

Соответствия можно задавать графически (рис. 1.14).

Обратное соответствие получается изменением направления стре-

лок.

3

Рис. 1.13. Графическое изображение соответствий

Композицией соответствий называется последовательное применение двух соответствий. Эта операция производится с тремя множествами А,В,С, на которых определены соответствия: g=(А,В,G), G A B и p=(B,C,P), Р B A, причем область значений первого соответствия совпадает с областью определения второго соответствия, т.е. Пр2G= Пр1Р. Первое соответствие для любого элемента а Пр1G определяет некоторый, возможно не единственный, элемент b Пр2G. Второе соответствие найденному элементу b Пр2G сопоставляет значение элемента c Пр2Р. Следовательно, композиция соответствий сопоставляет каждому элементу а из области определения первого соответствия, т.е. Пр1G, один или несколько элементов с из области значений второго соответствия, т.е. Пр2Р. Обозначается композиция g(p), а график композиции - G P. При этом композиция соответствий g и p запишется в виде g(p) = (A,C,G P), G P А С. Операцию композиции можно распространить на большее количество множеств.

1.4.Функция. Отображение множеств

1.4.1.Основные определения

Пусть даны множества А и В. Говорят, что на множестве А определена функция f, принимающая значения из множества В, если каждому элементу х из области определения функции поставлен в соответствие один и только один элемент y из области значений, т.е. функция f представляет собой функциональное соответствие между множествами А и В.

Если функция f каждому элементу х из А ставит в соответствие один и только один элемент y из В, то функция f называется отображением множества А в В.

Если сравнивать операцию соответствия и отображения, то можно сказать, что отображение - это функциональное, всюду определенное соответствие g=(A,B,G), где G={(x, f (x)) | x A, f (x) B}, т.е. G A B, Пр1G=А.

4

Для обозначения отображения из множества А в множество В используется запись: f : A B.

Если х А, то соответствующий ему элемент y=f(x) из В называется

образом элемента х при отображении f.

Совокупность образов всех элементов х, принадлежащих некоторому множеству С А, называется образом множества С, т.е. f(С)=

f (x) .

x C

Совокупность всех элементов х из множества А, образом которых является элемент y из множества В, называется прообразом элемента y при отображении f.

Аналогично определяется прообраз множества D B, т.е. объединение прообразов всех элементов из D.

Если образ множества А, т.е. f(A), состоит из одного элемента, то функция f называется функцией-константой.

Если отображение f имеет вид: f : A А, то такое отображение называется преобразованием множества А.

Если отображение f : A A задается в виде f(x)=x, то такое отображение называется тождественным.

Два отображения f : A B и f1 : A1 B1 называются равными, если области определения этих отображений совпадают, т.е. А=А1 и для любого элемента х А выполняется условие f(x)=f1(x).

Пример.

1)Функция f (x)=3х является отображением R в R, т.е. 3х : R R;

2)Функция f (x)= sin x является отображением множества R в

[1;1], т.е. sinx: R [-1;1].

Если множество А конечно, т.е. А={a1,...,an}, то отображение можно

f(ai) B, i=1,…,n.

1.4.2.Виды отображений

Отображение f : A B называется сюръективным или сюръекцией, если для любого элемента y B существует хотя бы один х А, который является его прообразом, т.е. y=f (x). В этом случае говорят, что f отображает

А на В.

Если f – сюръективное отображение, то f(A)=B.

В общем случае, когда f(A) B, то говорят, что f отображает множество А в множество В.

5

Отображение f : A B называется инъективным или инъекцией, если для любого y B его полный прообраз содержит не более одного элемента. Другими словами, отображение f : A B инъективно, если для любых элементов x1, x2 A и x1 x2 выполняется условие: f (x1) f (x2) (разным элементам соответствуют разные образы).

Отображение f : A B называется взаимно однозначным или биективным (биекция), если оно является одновременно сюръективным и инъективным. В этом случае условие y=f (x), где y – любой элемент множества В, однозначно определяет единственный элемент x A (рис. 1.15).

Функция типа f : A1 A2 … An B называется n-местной функцией. В этом случае принято считать, что функция (отображение) имеет n ар-

гументов, т.е. f (a1,a2,…,an), ai Ai, i=1,…,n..

Пример.

1)Сложение, умножение, вычитание и деление являются двухместными функциями на R, т.е. имеют тип R2 R.

2)Таблица выигрышей лотереи – двухместная не полностью определенная функция, которая устанавливает соответствие между парами

из N2 (серия, номер) и множеством выигрышей М, т.е. имеет вид N N М.

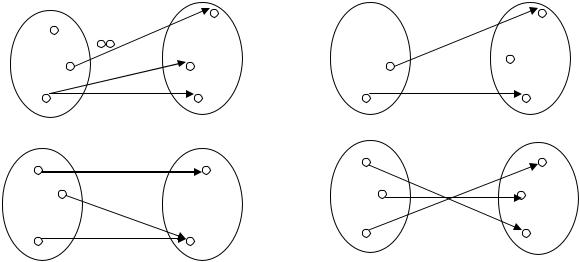
Рис. 1.14. Различные виды отображений: а) соответствие, но не отображение; в) инъективное, но не сюръективное отображение, с) не инъективное, но сюръективное отображение; d) биективное отображение

Если соответствие, обратное к функции f : А В, является функциональным, то оно называется функцией (или отображением), обратной к функции f, обозначаемой f -1: В А.

6

Т.к. в обратной функции образы и прообразы меняются местами, то для того, чтобы существовала обратная функция f –1, необходимо и достаточно, чтобы функция f была взаимно однозначной.

Пример.

Функция sin x: R [-1,1] не является взаимно однозначной, поэтому обратной функции для указанной функции не существует. Если функция sin x имеет тип sin x: [- /2; /2] [-1,1], то она является взаимно однозначной, поэтому на отрезке [-1,1] для нее существует обратная функция y=arcsin x.

1.4.3.Композиция функций

Пусть даны две функции f : A B и g: B С. Тогда функция h: A C называется композицией функций f и g (обозначается h=f g), если для любого х А выполняется равенство h(x) = g(f(x)).

Композиция f и g представляет собой последовательное выполнение двух функций: g применяется к результату f. Часто говорят, что h получается подстановкой функции f в g. Знак аналогично умножению часто опускается.

Для многоместных функций f: Am B и g: Bm C возможны различные варианты подстановки f в g, в результате чего получаются функции различных типов.

Пример.

Пусть m=2, а n=3. Тогда композицию можно задать так: h1=g(f(x1,x2), y1, y2). Эта функция имеет четыре аргумента и имеет тип h1:A2 B2 C. Другой вариант композиции: h2=g(f(x1,x2), y1, f(x1/,x2/)). Эта функция имеет уже пять аргументов и имеет тип h2: A2 B А2 C.

Особый интерес представляет случай, когда имеется множество функций вида

f1: Am1 A;

. . .

fn: Amn A.

В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых – любые переименования аргументов, например, переименование переменной х2 в х1 преобразует функцию двух переменных f(x1,x2) в функцию одной переменной f(x1,x1).

Функция, полученная из функций f1,..., fn с помощью некоторой подстановки их друг в друга или переименования переменных, называется суперпозицией. Выражение, описывающее эту суперпозицию и содержащее функциональные знаки, символы переменных и скобки, называется

формулой.

7

Пример.

Рассмотрим функции f(x)=2x и g(x)=1+x. Пусть эти функции имеют тип R R; поэтому их композиции возможны в произвольном порядке.

Композиция функций h1=f g представляет собой подстановку f в g,

т.е. h1= f g= g(f(x))=1+ f(x)=1+2x.

Композиция g f= h2 есть функция, полученная подстановкой g в f,

т.е. h2=g f= f(g(x))=2g(x)=2(1+x)=2+2x.

Функции h1 и h2, являющиеся композицией функций f и g, имеют область определения, совпадающую с областью определения исходных функций, т.е. R. В общем случае область определения композиции может быть более узкой, чем области определения обеих исходных функций, и даже может оказаться пустой.

Элементарной функцией в математике называется любая функция f, являющаяся суперпозицией фиксированного числа арифметических операций, а также функций ex, log x, sin x и т.д.

Например, функция f(x)=sin2 (x1+x2) является элементарной функцией, т.к. представляет собой суперпозицию функций f1 (x)=х2, f2 (x)=sin x, f(x1,x2)=x1+x2, т.е. f(x)= f1 (f2 (f3 (x1,x2))).

1.4.4.Способы задания функций

Существуют следующие способы задания функций:

1)Графический.

2)Табличный.

Функция задается конечным списком пар (х, f(x)), поэтому таким образом могут быть заданы только функции, определенные на конечных множествах. Таблицы функций, определенных на бесконечных множествах (например, тригонометрические функции), задают эти функции только в конечном числе точек. Для вычисления значений функций в промежуточных точках нужно воспользоваться методами интерполирования.

3)Аналитический.

Вэтом случае функция задается в виде формулы, которая описывает ее как суперпозицию других (исходных) функций. Если способ вычисления исходных функций известен, то формула задает процедуру вычис-

8

ления данной функции как некоторую последовательность вычислений исходных функций.

4) Рекурсивная процедура

Вычисление значения функций по графикам, таблицам, формулам являются частным видом вычислительных процедур. Существуют вычислительные процедуры, не относящиеся к указанным трем видам. Среди них следует выделить рекурсивные процедуры.

Рекурсивная процедура задает функцию на множестве натуральных чисел N следующим образом:

задается значение f(0) или f(1);

значение f(n+1) определяется через f(n) и все предыдущие,

которые считаются известными.

Например, задание функции f(x)= n! :

0!=1;

(n+1)!=n!(n+1).

Это тоже формула, однако, она отличается от тех формул, которые были рассмотрены ранее. Отличие состоит в том, что для вычисления (n+1)! требуется вычислить n!, в то время как по обычной формуле значение функции для любых допустимых значений аргументов вычисляется непосредственно.

1.5.Отношения

1.5.1.Основные определения

Сотношениями в математике мы встречаемся достаточно часто. Это и отношение равенства, определенное на любом множестве, и отно-

шение неравенства ( , , , ) на множестве вещественных чисел R, и отношение подобия фигур на плоскости и т.п.

Отношение – это один из способов задания взаимосвязей между элементами множества. В общем случае рассматриваются n-местные от-

ношения.

Под n-местным отношением понимают подмножество R прямого произведения n множеств: R М1 М2 … Мn . Будем говорить, что эле-

менты а1, а2,…, аn, (а1 М1, а2 М2,…, аn Мn) находятся в отношении R, если кортеж (а1, а2,…, аn) R . Если М1=М2=…=Мn=М, то R Мn.

Многоместные отношения используются, например, в теории баз данных. Само название «реляционная» база данных происходит от слова relation (отношение).

Наиболее изученными являются так называемые унарные и бинарные отношения.

9

Унарные (одноместные) отношения отражают наличие опреде-

ленного признака (свойства) у элементов множества М (например, «быть черным» на множестве шаров; «быть четным» на множестве чисел). Тогда все элементы а М, обладающие признаком R, образуют некоторое подмножество множества М, которое и называется унарным отношением, т.е.

а R и R М.

Чаще термин «отношение» используется для двухместных отноше-

ний (n=2).

Бинарные (двухместные) отношения используются для опреде-

ления взаимосвязей, которыми характеризуются пары элементов в множестве М (например, отношения «учиться в одной группе», «быть моложе», «быть отцом», введенные на множестве людей). Тогда все пары (а, b) элементов из М, между которыми имеет место отношение R, образуют подмножество пар из множества всех возможных пар элементов М М=М2, ко-

торое называется бинарным отношением R, т.е. (а, b) R, и при этом

R М М.

1.5.2.Бинарные отношения

Бинарным отношением R между множествами М1 и М2 называется подмножество прямого произведения М1 и М2, т.е. R М1 М2. Множество D(R)={a М1 (a,b) R} называется областью определения отношения R, а

множество Q(R)={b М2 (a,b) R} – областью значений. Если М1=М2= М, то R М М. Если а и b находятся в отношении R, то для записи этого будем в дальнейшем использовать инфиксную форму: aRb.

Способы задания бинарных отношений – любые способы задания множеств (это следует из того, что отношения есть подмножества прямого произведения множеств). Поэтому отношения на конечных множествах могут задаваться:

1)списком (перечислением) пар, для которых это отношение выполняется; например, R={(a,b), (a,d), (b,c)};

2)указанием свойства, которому удовлетворяют элементы a и b;

например, R={(a,b) a А, b B, b a}; 3) с помощью матрицы.

Матрицей бинарного отношения R, заданного на множестве

М={а1, а2,…, аn}, называется квадратная матрица С={cij}nxn порядка n, в которой элемент сij определяется следующим образом:

Матрица С называется матрицей инцидентности бинарного отношения.

10