Аналитическая геометрия на плоскости

Содержание

1. Система координат на плоскости

   1. Основные понятия

   2. Основные приложения метода координат на плоскости

      1. Расстояние между двумя точками

      2. Деление отрезка в данном отношении

      3. Площадь треугольника

   3. Преобразование системы координат

      1. Параллельный перенос осей координат

      2. Поворот осей координат

2. Линии на плоскости

   1. Основные понятия

   2. Уравнения прямой на плоскости

      1. Уравнение прямой с угловым коэффициентом

      2. Общее уравнение прямой

      3. Уравнение прямой, проходящей через данную точку в данном направлении

      4. Уравнение прямой, проходящей через две точки

      5. Уравнение прямой в отрезках

      6. Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору

      7. Полярное уравнение прямой

      8. Нормальное уравнение прямой

   3. Прямая линия на плоскости. Основные задачи

      1. Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых

      2. Расстояние от точки до прямой

1. Система координат на плоскости

а. Основные понятия

Что такое система координат? Это численный способ описания положения точки. Одной из таких систем является прямоугольная (декартова) система координат.

Система из себя представляет две взаимно перпендикулярные прямые (оси координат), имеющие определенный масштаб. Ось Ox - ось абсцисс; ось Oy - ось ординат. Эти две оси делят любую плоскость на четыре области - четверти (или квадраты).

Единичные векторы осе обозначают i и j. Плоскость, в которой распложена система называют координатной плоскостью.

Координаты точки М - координаты радиуса-вектора ОМ. Они имеют вид М(х,у). Х - абсцисса, а У - ордината точки М.

Для определения положения точки используют метод координат. Его сущность состоит в том, что для каждой линии в плоскости сопоставляется ее уравнение.

Есть и иная не менее важная система координат. А именно полярная. Задается она полюсом (точ. О), полярной осью (луч Ор) единичным вектором е сонаправленным с Ор.

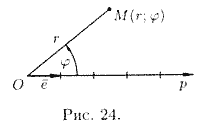
Положение точки М определяется радиусом r и углом фи. Эти числа (r and fi) называются полярными числами точки М, обозначают М (r; fi), где r - полярный радиус, fi -полярным углом. r ограничивается отрезком - [0, +бесконечность), а fi - (-pi;pi].

Связь между полярной и декартовой системами координат можно представить в виде:

Определяя величину φ, следует установить (по знакам x и у) четверть, в которой лежит искомый угол, и учитывать, что - < φ< .

b. Основные приложения метода координат на плоскости.

i. Расстояние между двумя точками.

Расстояние между точками А и В есть длина вектора АВ.

ii. Деление отрезка в данном отношении.

...

iii. Площадь треугольника

....

c. Преобразование системы координат

Это переход от одной системы координат в какую-либо другую. Есть два способа преобразования.

i. Параллельный перенос осей координат.

Параллельный перенос осей координат - переход от системы Oxy к новой системе O₁x₁y₁.

ii. Поворот осей координат

Преобразование координат, при котором обе оси поворачиваются на один и тот же угол. При этом масштаб и начало координат не изменяются.

Эти формулы называются формулами поворота осей.

2. Линии на плоскости

a. Основные понятия

Линия - это множество точек.

Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел — ее координат, а положе­ние линии на плоскости определять с помощью уравнения (т. е. равенства, связывающего координаты точек линии).

Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты x и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Переменные x и у в уравнении линии называются текущими коорди­натами точек линии.

Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения.

Так, для того чтобы установить лежит ли точка А(x0; у0) на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки А уравнению этой линии в выбран­ной системе координат.

Задача о нахождении точек пересечения двух линий, заданных урав­нениями F1(x1;y1) = 0 и F2(x2;y} = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:

Если эта система не имеет действительных решений, то линии не пересекаются.

Аналогичным образом вводится понятие уравнения линии в полярной системе координат.

Уравнение F(r; φ)=О называется уравнением данной линии в поляр­ной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать при помощи двух уравнений:

где x и у — координаты произвольной точки М(х; у), лежащей на данной линии, а t — переменная, называемая параметром; параметр t определяет положение точки (х; у) на плоскости.

Например, если x = t + 1, у = t2, то значению параметра t = 1 соот­ветствует на плоскости точка (3; 4), т. к. x = 1 + 1 = 3, у = 22 - 4.

Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется параметрическим, а уравнения (10.1) — параметрическими уравнениями линии.

Чтобы перейти от параметрических уравнений линии к уравнению вида F(x;y) = 0, надо каким-либо способом из двух уравнений исключить параметр t.

Например, от уравнений путем подстановки t = х

во второе уравнение, легко получить уравнение у = х2; или у-х2 = 0, т. е. вида F(x; у) = 0. Однако, заметим, такой переход не всегда возможен.

В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти ее уравнение) вторая: зная уравнение кривой, изучить ее форму и свойства.

b. Уравнения прямой на плоскости:

i. Уравнение прямой с угловым коэффициентом

Из определения тангенса угла следует равенство

Введем обозначение tg a=k, получаем уравнение

Число k = tga называется угловым коэффициентом прямой, а уравнение (10.2) — уравнением прямой с угловым коэффициентом.

Если прямая параллельна оси Ох, то a = 0, следовательно, k = tga = 0 и уравнение (10.2) примет вид у = b.

ii. Общее уравнение прямой.

Рассмотрим уравнение первой степени относительно x и y в общем виде

Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.

iii. Уравнение прямой, проходящей через данную точку в данном направлении

Уравнение (10.5) с различными значениями k называют также уравнениями пучка прямых с центром в точке Из этого пучка нельзя определить лишь прямую, параллельную оси Оу.

iv. Уравнение прямой, проходящей через две точки:

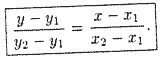
v. Уравнение прямой в отрезках:

Это уравнение называется уравнением прямой в отрезках, так как числа α и b указывают, какие отрезки отсекает прямая на осях координат.

vi. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору:

уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

Уравнение (10.8) можно переписать в виде:

vii. Полярное уравнение прямой:

Для любой точки  на данной прямой имеем:

С другой стороны:

Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.

viii. Нормальное уравнение прямой:

Уравнение (10.11) называется нормальным уравнением прямой.

c. Прямая линия на плоскости. Основные задачи

i. Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых:

ii. Расстояние от точки до прямой: