Передач с эвольвентным профилем зубьев

 

Межосевое расстояние при (см. рис. 31) или.

Приняв суммарное число зубьев найдем .

В прямозубой передаче ширина венца равна длине зуба:, где— коэффициент длины зуба (ширины венца) по модулю (для цилин­дрических прямозубых передач); выбирается по табл. 2.

 

Таблица 4. Значение коэффициента

, не более	HB	Характеристика конструкции
45-30 30-20	До 350 Свыше 350	Высоконагруженные точные передачи. Валы, опоры и корпуса повышенной жесткости
30-25 20-15 15-10	До 350 Свыше 350	Обычные передачи редукторного типа в отдельном кор­пусе с достаточно жесткими валами и опорами. Передачи низкой точности с консольными валами

 

Таблица 5. Геометрические параметры прямозубой цилиндрической передачи

Параметр, обозначение	Расчетные формулы
Модуль т
Диаметр вершин зубьев da
Делительный диаметр d
Диаметр впадин зубьев df
Высота зуба h
Высота головки зуба ha
Высота ножки зуба hf
Окружная толщина зуба
Окружная толщина впадин зубьев
Радиальный зазор с
Межосевое расстояние
Окружной шаг рt
Длина зуба (ширина венца)

 

Определение числа зубьев шестерни и колеса по суммарному числу зубьев передачи и известному передаточному числу. Если известно и , то число зубьев шестерни и колеса можно определить по формулам:

; ,

где — число зубьев шестерни;— число зубьев колеса;— суммарное число зубьев;и — передаточное число.

 

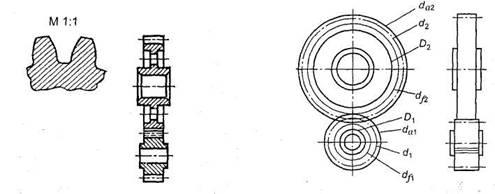
Рис. 32 Рис. 33

 

Расчет зубьев цилиндрической прямозубой передачи на изгиб ?

Расчет цилиндрической прямозубой передачи на контактную прочность?

Цилиндрические косозубые и шевронные зубчатые передачи. Устройство и основные геометрические и силовые соотношения

Косозубые зубчатые передачи, как и прямозубые, предназначены для передачи вращательного момента между параллельными валамя (рис. 36). У косозубых колес оси зубьев располагаются не по образующей делитель­ного цилиндра, а по винтовой линии, составляющей с образующей угол (рис. 37). Угол наклона зубьев р принимают равным , он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.

Рис. 36. Цилиндрическая косозубая передача

 

Передаточное число для одной пары колес может быть . В прямозубых передачах линия контактапараллельна оси, а в косозубых расположена по диа­гонали на поверхности зуба (контакт в прямозубых передачах осуществляется вдоль всей длины зуба, а в косозубых — сначала в точке увеличивается до пря­мой, «диагонально» захватывающей зуб, и постепен­но уменьшается до точки).

Достоинства косозубых передач по сравнению с прямозубыми: уменьшение шума при работе; меньшие габаритные размеры; высокая плавность зацепления; большая нагрузочная способность; значительно меньшие дополнительные дина­мические нагрузки.

За счет наклона зуба в зацеплении косозубой передачи появляется осевая сила.

Направление осевой силы зависит от на­правления вращения колеса (рис. 37), на­правления винтовой линии зуба, а также от того, каким является колесо — ведущим или ведомым. Осевая сила дополнительно нагру­жает валы и опоры, что является недостатком косозубых передач.

 

Рис. 37. Усилия в косозубой цилиндрической передаче

 

Шевронные зубчатые колеса пред­ставляют собой разновидность косозубых колес (рис. 38).

 

а) б)

Рис. 38. Шевронная зубчатая передача

 

Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (рис. 38, а), называют шеврон­ным колесом. Часть венца зубчатого колеса, в пределах которого линии зубьев имеют одно направление, называют полушевроном. Различают шев­ронные колеса с жестким углом (рис. 38, б), предназначенным для выхо­да режущего инструмента при нарезании зубьев. Шевронные передачи об­ладают всеми преимуществами косозубых, а осевые силы (рис. 39) проти­воположно направлены и на подшипник не передаются.

 

Рис.39. Усилия в зацеплении шевронных зубчатых колес

 

В этих передачах допускают большой угол наклона зубьев ().Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т.е. в тех случаях, когда требует­ся передавать большую мощность и высокую скорость, а осевые нагрузки нежелательны.

Рис. 40

 

Косозубые и шевронные колеса в отличие от прямозубых имеют два шага и два модуля: в нормальном сечении (см. рис. 44) по делительной окружности — нормальный шаг р_п, в торцовой плоскости — торцовый шаг р_t. Из условия, что модуль зацепления равен шагу, деленному на число , имеем; .

Для косозубых и шевронных колес значения нормального модуля т_n стандартизованы, так как профиль косого зуба в нормальном сечении со­ответствует исходному контуру инструментальной рейки и, следовательно, т = т_п (косозубые и шевронные колеса нарезают, тем же способом и инст­рументом, что и прямозубые). Нормальный модуль т_п является исходным при геометрических расчетах.

Определим зависимость между нормальным и торцовым шагом и модулем через угол наклона зубьев.

Если левую и правую части разделим на , получим

; .

Геометрические параметры цилиндрической косозубой и шевронной передач с эвольвентным профилем зуба рассчитают по формулам, приве­денным в табл. 15. По торцовому модулю т_t рассчитывают делительные (начальные) диаметры, а до т_п — все остальные размеры зубчатых колес.

 

Таблица 15. Геометрические параметры цилиндрической косозубой передачи

Параметр, обозначение	Расчетные формулы
Нормальный модуль
Торцовый (окружной модуль)
Диаметр вершин зубьев в
Делительный диаметр d
Диаметр впадин зубьев
Шаг нормальный
Шаг торцовый (окружной)
Окружная толщина зубьев
Ширина впадин зубьев
Высота зуба
Высота головки зуба
Высота ножки зуба
Радиальный зазор
Межосевое расстояние
Длина зуба
Ширина венца

 

Окружная сила . На косой зуб действует осевая сила (см. рис. 37), радиальная (распорная) сила.

В косозубдй передаче сила , действующая на зуб косозубого колеса(см. рис. 44), направлена по нормали к профилю зуба, т.е. по линии зацепле­ния эквивалентного прямозубого колеса, и составляет угол с касательной кэллипсу.

Эту силу разложим на две составляющие: окружную силу на эквива­лентном колесе и радиальную (распорную) силу на этом колесе .

Если, в свою очередь, силу разложить по двум направлениям, то по­лучим такие силы: — окружную силу, — осевую.

Для зубчатого колеса с шевронным зубом окружную силу и рас­порную определяют по тем же формулам, что и для косозубой передачи т.е. , . В шевронной передаче осевая сила (см. рис. 39).

 

Винтовая передача (разновидность ко­созубой) состоит из двух косозубых цилиндри­ческих колес (рис. 41). Однако в отличие от косозубых цилиндрических передач с парал­лельными валами касания между зубьями здесь происходит в точке и при значительных скоро­стях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.

Рис.41. Винтовая зубчатая передача

 

Рис. 42

 

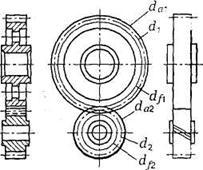
Рис. 43

 

Расчет зубьев цилиндрической косозубой и шевронной передач на изгиб?

 

Расчет цилиндрической косозубой и шевронной передач на контактную прочность?

Последовательность проектировочного расчета цилиндрической косозубой передачи

Последовательность приведенного расчета аналогична расчету цилинд­рической прямозубой передачи.

Последовательность расчета закрытой цилиндрической косозубой передачи.

1. Определить передаточное число .

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и твердость рабочих поверхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую долговечность, определить допускаемые напряжения изгиба и контактные напряжения.

4. Выбрать коэффициент длины зуба (ширины венца колеса).

5. Определить межосевое расстояние из условия контактной прочности по формуле (26).

6. Задать значение нормального модуля из соотношения и округлить его до ближайшего стандартного значения (см. табл. 3). При этом для силовых передач желательно иметь модуль не ме­нее 1,5—2 мм.

7. Задать угол наклона зубьев и определить суммарное число зубьев, передачи, числа зубьев шестерни и колеса и .

8. Определить эквивалентные числа зубьев и и коэффициенты фор­мы зуба и.

9. По формуле (23) проверить прочность зубьев по напряжениям из­гиба. При неудовлетворительных результатах (или) необ­ходимо путем соответствующего изменения числа зубьев и модуля при том же межосевом расстоянии добиться определенного изменения напряжения изгиба, не нарушая условия контактной прочности.

10. Произвести геометрический расчет передачи (см. табл. 15). Опре­делить окружную скорость колес и по табл. 14 назначить соответствую­щую степень точности, выбрать (табл. 16).

Расчет открытых передач (часто открытые передачи рассчитыва­ют так же, как закрытые).

1. Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы для колес, назначить их термическую обработку и твердость рабочих поверхно­стей зубьев.

3. Определить базу испытаний базового числа циклов , расчетную циклическую нагрузку, вычислить коэффициенты и определить допускае­мые напряжения изгиба.

4. Задать угол наклона зубьев и число зубьев шестерни

5. Определить число зубьев колеса

6. Определить числа зубьев эквивалентных колес, шестерни и колеса и по табл.6 коэффициенты формы зуба и.

7. Выбрать — коэффициент длины зуба (ширины венца).

8. Из условия прочности на изгиб определить по формуле (24) значе­ние нормального модуля и округлить до ближайшего большего стан­дартного значения (см. табл. 3).

9. Произвести геометрический расчет передачи (см. табл. 15).

10. Определить окружную скорость колес и по табл. 14 назначить соответствующую ей степень точности.

 

Конические зубчатые передачи. Устройство и основные геометрические и силовые соотношения

Зубчатую передачу с пересекающимися осями, у которой начальные и делительные поверхности колес конические, называют конической.

Коническая передача состоит из двух конических зубчатых колес (рис. 45) и служит для передачи вращающего момента между валами с пересекающимися осями под углом . Наиболее распространена вмашиностроении коническая передача с углом между осями Z=90⁰ (рис. 47), но могут быть передачи и с . Колеса конических передач. выполняют с прямыми (рис. 46, а), косыми (рис. 46, б), круговыми зубьями (рис. 46, в).

 

Рис. 45. Коническая пря­мозубая передача

 

Рис. 46. Конические зубчатые колеса: а — коле­со с прямыми зубьями;

б — колесо с косыми зу­бьями; в — колесо с круговыми зубьями

 

Рис. 47. Геометрические параметры конических зубчатых колес

 

Рис. 48. Гипоиднаяя передача

 

Передачу с коническими колесами для передачи вращающего момента между валами со скрещиваю­щимися осями называют гипоидной (рис. 48). Эта передача находит применение в автомобилях.

По стоимости конические передачи дороже ци­линдрических при равных силовых параметрах. Их применение диктуется только необходимостью пе­редавать момент при пересекающихся осях валов. Передаточное число одной пары .

 

Вершины начальных и делительных конусов конической передачи на­ходятся в точке пересечения осей валов О (рис. 50). Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи (рис. 47 и 50):

АОВ — делительный конус шестерни;

ВОС — делительный конус колеса;

АО₁В — делительный дополнительный конус шестерни;

ВО₂С — делительный дополнительный конус колеса;

— угол делительного конуса шестерни;

—угол делительного конуса колеса;

d_e[ — внешний делительный диаметр шестерни;

d_e2 — то же, колеса;

d₁ — средний делительный диаметр шестерни;

d₂ — то же, колеса;

b — ширина зубчатого венца (длина зуба);

R_e — внешнее делительное конусное расстояние (или длина дис­танции).

Рис. 50. Коническая прямозубая передача

 

Передаточное число конической передачи определяется так:

В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают внешнюю и среднюю делительные окружности (см. рис. 47).

Из условия, что в конической передаче модуль и делительный связаны теми же соотношениями, что и в цилиндрических передачах, т.е. d=mz (рис.51), определяют внешний d_e и средний d_m делительные метры:

где т_е — внешний окружной модуль; т_т — средний окружной модуль.

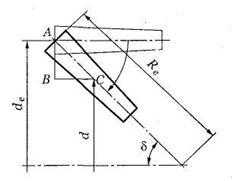
Рис. 51. Зуб конического колеса

 

Внешний окружной модуль обычно выбирают из стандартного ряда (см. табл. 3). Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все геометрические параметры зубча­тых колес (задают размеры зубьев на внешнем торце, на котором удобно производить измерения).

Средний окружной модуль т рассчитывают в зависимости от внешнего окружного модуля т_е. По среднему окружному модулю производят расчет передачи на прочность при изгибе.

Рис. 52

 

Зависимость между т_е и т_т в конической передаче.

Из рис. 3.51 , где (из). Отсюда .

Умножив левую и правую части равенства на два, получим .Разделив левую и правую части равенства на , получим

или

Геометрические соотношения размеров прямозубой конической пере­дачи с эвольвентным профилем зуба. Согласно рис. 53 внешний диаметр вершин зубьев

внешний диаметр впадин зубьев

Длина зуба (ширина венца) [при условиии, где — средний делительный диаметр шес­терни].

Рис. 53. Геометрия прямозубой конической передачи

 

Ориентировочно длина зуба может быть выбрана также в зависимости от внешнего делительного конусного расстояния R_e:

.

 

Таблица 17. Геометрические параметры прямозубой конической передачи

Параметр, обозначение	Расчетные формулы
Внешний окружной модуль
Средний окружной модуль
Внешний диаметр вершин зубьев
Внешний делительный диаметр
Внешний диаметр впадин зубьев
Высота зуба
Высота головки зуба
Высота ножки зуба
Окружной шаг
Окружная толщина зуба
Окружная ширина впадины
Радиальный зазор
Ширина зубчатого венца
Внешнее делительное конусное расстояние
Угол делительного конуса шестерни
колеса

 

Силы в зацеплении прямозубой конической передачи. В рассматривае­мой передаче действует одна сила, обусловленная давлением зуба шестерни на зуб колеса. Эта сила для удобства расчетов раскладывается на 3 состав­ляющие: окружная F_t, радиальная F_r и осевая F_a.

С учетом геометрических соотношений в конической передаче по нор­мали к зубу действует сила F_n1 (рис. 54). Эту силу разложим на две состав­ляющие: и . В свою очередь разложим на и . Запишем:

; ; .

Осевая сила на шестерне численно равна радиальной силе на колесе.

Рис. 54. Силы в зацеплении прямозубой конической передачи

Рис.55

 

Рис. 56

 

Расчет зубьев прямозубой конической передачи на изгиб?

 

Расчет конических прямозубых передач на контактную прочность?

Последовательность проектировочного расчета конической зубчатой передачи

Последовательность расчета закрытой передачи.

1. Определить передаточное число и углы делительных конусов шес­терни и колесаи.

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и значения твердости рабочих по­верхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую дол­говечность , коэффициенты режима, допускаемые контактные напряже­ния и допускаемые напряжения изгиба.

4. Выбрать коэффициент длины зуба.

5. Определить средний делительный диаметр из условия контактной прочности [формула (32)].

6. Задать число зубьев шестерни , определить число зубьев колеса

7. Рассчитать внешний модуль , и округлить его до стандартного зна­чения (см. табл. 3), а также средний модуль .

8. Определить числа зубьев эквивалентных колес и и по табл. 8 — коэффициенты формы зуба шестерни и колеса .

9. Проверить прочность зубьев по напряжениям изгиба. При неудовле­творительных результатах необходимо путем соответствующего изменения числа зубьев и модуля при том же конусном расстоянии до­биться определенного изменения напряжений изгиба, не нарушая при этом условия контактной прочности.

10. Произвести геометрический расчет передачи (см. табл. 17).

11. Определить окружную скорость колес и по табл. 14 назначить со­ответствующую степень точности.

Последовательность расчета открытых конических передач.

1. Определить передаточное число и углы делительных конусов шестерни и колесаи.

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и значения твердости рабочих по­верхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую дол­говечность, коэффициенты режима и определить допускаемые напряжения изгиба.

4. Задать число зубьев шестерни и по передаточному числу опреде­лить число зубьев колеса .

5. Определить число зубьев эквивалентных колес и коэффициен­ты формы зуба и по табл. 8.

6. Выбрать коэффициент длины зуба (ширины венца) .

7. Из условия прочности на изгиб (формула 29) определить средний модуль , после чего подсчитать внешний модуль , значение которого округлить до ближайшего большего стандартного (см. табл. 3). При необ­ходимости следует пересчитать в зависимости от стандартного .

8. Произвести геометрический расчет передачи (см. табл. 17).

9. Определить окружную скорость колес и по табл. 14 назначить со­ответствующую степень точности зацепления.

 

Зубчатые передачи с зацеплением Новикова. Устройство, основные геометрические соотношения ?

Достоинства и недостатки передач с зацеплением Новикова. Высо­кая нагрузочная способность является основным достоинством передач с зацеплением Новикова. При твердости рабочих поверхностей до НВ 350 можно принимать допускаемую нагрузку примерно в 2,5 раза больше до­пускаемой нагрузки для эвольвентных прямозубых передач тех же основ­ных размеров, выполненных из тех же материалов, с той же термической обработкой (сравнение допускаемых нагрузок произведено при коэффици­енте нагрузки К= 1).

Благодаря большей нагрузочной способности передачи с зацеплением Новикова более компактны, имеют почти в 2 раза меньшие габариты по сравнению с передачами с эвольвентным зацеплением при одинаковой пе­редаваемой мощности.

Передачи с зацеплением Новикова допускают большее передаточное число, а вследствие хорошо удерживающейся масляной пленки между со­прикасающимися зубьями уменьшается изнашивание зубьев, повышается КПД передачи.

Потери на трение в зацеплении Новикова примерно в 2 раза меньше, чем потери в эвольвентном зацеплении. Шум во время их работы значи­тельно ниже.

Недостатками являются:

- большая (чем в эвольвентных зацеплениях) чувствительность к изме­нению межосевого расстояния;

- с увеличением нагрузки в зацеплении возрастает осевая составляю­щая, что, в свою очередь, усложняет конструкцию применяемых подшипниковых узлов;

- при ухудшении контакта (например, в случае перекоса валов и изме­нения межосевого расстояния) вся нагрузка, действующая на зубья, может сосредоточиться на небольшом участке длины зубьев, в ре­зультате чего зубья могут оказаться сильно перегруженными;

- необходимость иметь две специальные фрезы для нарезания зубьев (для шестерни и колеса).

а)

Рис. 59. Косозубая передача с зацеплением М.Л. Новикова

 

Расчет передачи с зацеплением Новикова на контактную прочность?

Планетарные зубчатые передачи. Устройство передачи и расчет на прочность

Передачи, имеющие зубчатые или фрикционные колеса с перемещающимися осям, называют планетарными. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

Наиболее распространена зубчатая однорядная планетарная передача (рис.60). Она состоит из центрального колеса 1 с наружными зубьями, неподвижного (центрального) колеса 2 с внутренними зубьями и водила на котором закреплены оси планетарных колес g (или сателлитов).

Рис.60. Планетарная передача

 

Водило вместе с сателлитами вращается вокруг центральной оси, а са­теллиты обкатываются по центральным колесам и вращаются вокруг своих осей, совершая движения, подобные движению планет. При неподвижном колесе 2 движение передается от колеса 1 к водилу h или наоборот.

Планетарную передачу, совершаемую подвижными звеньями (оба иентральных колеса и водило), называют дифференциалом. С помощью диффе­ренциала одно движение можно разложить на два или два движения сло­жить в одно: от колеса 2 движение можно передавать одновременно колесу 1 и водилу h или от колес 1 и 2 к водилу g и т. д. Планетарную передачу ус­пешно применяют в транспортном машиностроении, станкостроении, приборостроении.

Достоинства и недостатки планетарных передач.

Основное достоинство — широкие кинематические возможности, по­зволяющие использовать передачу в качестве редуктора коробки скоро­стей, передаточное число в которой изменяется путем поочередного тормо­жения различных звеньев, и как дифференциальный механизм.

- Планетарный принцип позволяет получать большие передаточные чис­ла (до тысячи и больше) без применения многоступенчатых передач.

- Эти передачи компактные и имеют малую массу. Переход от простых передач к планетарным позволяет во многих случаях снизить их массу в 4 раза и более.

- Сателлиты в планетарной передаче расположены симметрично, а это снижает нагрузки на опоры (силы в передаче взаимно уравновешиваются), что приводит к снижению потерь и упрощает конструкцию опор.

- Эти передачи работают с меньшим шумом, чем обычные зубчатые и имеют более лёгкое управление и регулирование скорости;

- Имеют малый шум вследствие замыкания сил в механизме.

Основные недостатки: повышенные требования к точности изготовле­ния и монтажа (для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом); резкое снижение КПД передачи с увеличением передаточ­ного отношения.

Передаточное отношение.

Для определения передаточного отношения планетарной передачи ис­пользуется метод Виллиса — метод останова водила.

Передаточное отношение планетарной передачи (см. рис. 60)

(33)

где и— угловые скорости колес1 и 2 относительно води­ла h; и — числа зубьев этих колес.

Для реальной планетарной передачи (колесо 2 закреплено неподвиж­но, колесо 1 — ведущее, водило h ведомое) при из формулы (36) получим

или

(34)

Для однорядной планетарной передачи , для многоступен­чатых, для кинематических передач. Чем больше передаточное отношение планетарной передачи, тем меньше КПД (0,99...0,1).

Расчет на контактную прочность зубьев планетарных передач проводится по аналогии с расчетом обыкновенных зубчатых передач от­дельно для каждого зацепления (см. рис.60): пара колес 1—g (внешнее зацепление) и g—2 — (внутреннее). Для таких передач достаточно рассчи­тать только внешнее зацепление, так как модули и силы в зацеплениях одинаковые, а внутреннее зацепление прочнее внешнего.

Проектировочный расчет планетарной передачи на контактную ус­талость активных поверхностей зубьев проводится по следующей формуле:

(35)

где d₁ — делительный диаметр ведущего звена (шестерни), мм; K_d = 78 МПа — вспомогательный коэффициент (рассматриваются сталь­ные прямозубые колеса); T₂ — вращающий момент на шестерне, Нмм; — коэффициент нагрузки (см. табл.4); — коэффици­ент, учитывающий неравномерность распределения нагрузки среди сател­литов;— передаточное отношение;— коэффициент длины зуба (ширины колеса);— допускаемое контактное напряжение, МПа.

При расчете планетарных передач выбор числа зубьев колес зависит не только от передаточного отношения , но и от условийсобираемости пере­дач. При этом сумма зубьев центральных колес должна быть кратной числу сателлитов (лучше 3).

 

Волновые зубчатые передачи. Устройство передачи и расчет на прочность

Рис. 61. Волновая передача

 

Рис. 62. Трехволновая передача

 

Достоинство и недостатки волновых передач.

Волновые передачи обладают большой нагрузочной способностью (в за­цеплении находится большое число пар — зубьев) и высоким передаточным числом (< 300 для одной ступени) при сравнительно малых габаритах. Это основные достоинства этих передач. Передача может работать, находясь в герметизированном корпусе, что очень важно для использования волновых передач в химической, авиационной и других отраслях техники.

Недостатки волновой передачи: практически индивидуальное, дорогостоящее, весьма трудоемкое изготовление гибкого колеса и волнового генератора; возможность использования этих передач только при сравнительно невысокой угловой скорости вала генератора; ограниченные обороты ведущего вала (во избежание больших центробежных сил инерции некруглого генератора волн; мелкие модули зубьев 1,5-2 мм)

Волновые передачи можно применять в качестве редукторов, диффе­ренциалов и вариаторов скорости.