2. Моделирование производственных систем и процессов

2.1.Математическое.Моделирование.Амплитуда-фазовых частотных характеристик

Частотные характеристики звеньев систем автоматического управления.

Передаточная функция колебательного звена имеет вид:

k=15;

T=1,5;

ξ=0,2;

Найдем амплитудно-фазовую частотную характеристику. Для этого умножим числитель и знаменатель на сопряженный знаменатель и произведем упрощение с разделением действительной и мнимой части:

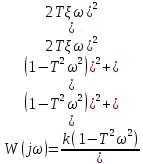
Пропорциональное звено с передаточной функцией имеет вид:

;

;

;

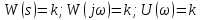Дифференцирующее звено имеет вид:

;

;

;

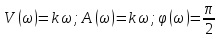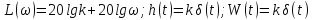Интегрирующее звено имеет вид:

;

;

;

Форсирующее звено первого порядка имеет вид:

;

;

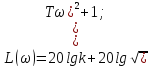Апериодическое звено имеет вид:

;

;

Форсирующее звено второго порядка имеет вид:

;

;

;

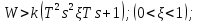
Колебательное звено имеет вид;

;

;

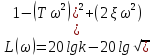Моделирование систем управления.

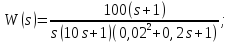-передаточная функция.

Составим логарифмическую амплитудно-частотную характеристику:

; -интегрирующее звено.

;

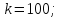
; -форсирующее звено первого порядка.

;

;

; -апериодическое звено.

;

;

;-колебательное звено.

;

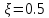
L(W)=;

L(W)=

В результате получаем логарифмическую амплитуда- частотную характеристику:

L(W)=L₁(W)+ L₂(W)+ L₃(W)+ L₄(W)

L(W)=

2.2 Компьютерное моделирование

Построение амплитудной-фазной частотной характеристики.

Набор исходных данных ,функции W графической каманды plot , команды визуализации сетки на графики grid-on

>>k=15;z=0.2;T=1.5; w=0:0.01:100;

W=k./(T.^2.*(w.*j).^2+2.*T.*z.*w.*j+1);

plot(real(W),imag(W),'-oK'), t

>>title('W(jw)=k./('T.^2.*(w.*j).^2+2.*T.*z.*w.*j+1);

k=15;z=0.2;T=1.5'),

xlabel('U=real(W)'),ylabel('jV=jimag(W)')

>> gtext('Wpac(jw)')

Построение характеристике и формирование надписей не ней производиться матлаб в отдельно окне представлено ниже .Команда grig on включает сетку ,grid of выключает сетку , title - заголовок графика. С помощи спецификатера кривой можно измерить тип Линии графика представить угловые точки различными отметками.

Рисунок.1. Амплитуда- частотная характеристика, построенная по командам.

Построение расчетных логарифмических частотных характеристик.

Характеристика набирается в командной строке в соответствии с цепочкой команд:

k=15;z=0.2;T=1.5; w=0.1:0.01:10;

L=20.*log10(k./sqrt((2.*T.*z.*w).^2+(1-T.^2.*w.^2).^2));

semilogx(w,L,'-B'),grid on

title('L=20log10(k./sqrt((2.*T.*z.*w).^2+(1-T.^2.*w.^2).^2)''ar=-(180./pi).*atan(2.*T.*z.*w./(1-T.^2.*w.^2));k=15;z=0.2;T=1.5'),

xlabel('log(w)'),ylabel('L')

hold on

w1=0.1:0.01:1;

ar1=-(180./pi).*atan(2.*T.*z.*w1./(1-T.^2.*w1.^2));

semilogx(w1,ar1,'-K')

xlabel('log(w1)'),ylabel('ar1')

hold on

w2=1:0.01:10;

ar2=-180-(180./pi).*atan(2.*T.*z.*w2./(1-T.^2.*w2.^2));

semilogx(w2,ar2,'-K')

xlabel('log(w2)'),ylabel('ar2')

После завершения набора нажимаем клавишу Enter завершающего ввод команды .MATLAB построит график. Расчетные логарифмические частотные характеристики представлены ниже.

Рисунок .2. Расчетные логарифмические частотные характеристики.

2.3 Математическая модель передаточной, переходной и весовой функции

Переходная функция системы(звена) - это функция описывающая реакцию системы на еденичное ступенчатое воздействие при нулевых начальных условиях.

Импульсная приходная (весовая) функция - это функция описывающая реакцию системы(звена) на единичное импульсное воздействие при нулевых начальных условиях.

Передаточная функция колебательного звена имеет вид:

Ей соответствует деферинциальное уравнение имеющее следующий вид:

+2ξ1)y=

Для определения переходной функции нужно решить это уравнение при входном воздействии u=1(t) и нулевых начальных условий:

+21)y=k*1(t);

нулевое условие:

y(0)=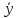(0)=0;

Характеристическое уравнение имеет следующий вид:

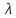+2T+1=0;

и его корнями являются:

=;

или:

j;

Положив α=

общее решение однородного деферинциального уравнения можно записать в следующем виде:

=(

Частное решение неоднородного уравнения:

=K;

поэтому общее решение будет иметь следующий вид:

y=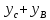=(+K;

Производная от этого решения имеет следующий вид:

[ (;

k=15;

ξ=0.2;

T=1,5;

Передаточная функция колебательного звена имеет вид:

=;

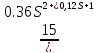Составим характеристическое уравнение.

Знаменатель функции приравняем к нулю:

D=0.16+1,2λ+1=0;

Находим дискриминант :

D=-0.36ac

D=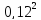-0.36*0.36*1

D= - 1,41<0 меньше нуля, значит пара комплексно-сопряженных корней:

=;

====

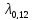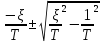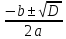Частное решение неоднородного решения:

=k= ;

Общее решение имеет следующий вид:

y=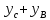=(+k

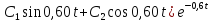y=(+16;

Производное общего решения дифиринциального уравнения имеет следующий вид:

[ (;

[(;

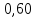Начальное условие принимает следующий вид:

;

; от суда:

;

Переходная функция имеет следующий вид:

k=[1 - или после элементарных

преобразований:

*sin(

где

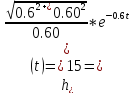*sin(

Весовая функция принимает следующий вид:

sin(;

=

=5.84*.