
- •Сборник практических занятий по дисциплине «элементы высшей математики»
- •230105 «Программное обеспечение вычислительной техники и автоматизированных систем»
- •Содержание
- •Пояснительная записка
- •Практическое занятие №1 Тема: Операции над матрицами. Вычисление определителей
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №2 Тема: Нахождение обратной матрицы
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №4 Тема: Решение систем алгебраических уравнений методом Гаусса
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №5 Тема: Операции над векторами. Вычисление модуля и скалярного произведения
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №6 Тема: Составление уравнений прямых и кривых второго порядка, их построение
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №7 Тема: Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №8 Тема: Вычисление односторонних пределов, классификация точек разрыва
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №9 Тема: Вычисление производных функций по определению производной
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №10
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №12 Тема: Полное исследование функции. Построение графиков
- •Теоретический материал
- •Задания для самостоятельной работы
- •Практическое занятие №13 Тема: Интегрирование заменой переменной и по частям в неопределенном интеграле
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №14 Тема: Вычисление определенных интегралов
- •Теоретический материал
- •Примеры
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №16
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №17
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №18
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №19
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №20
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №21
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №22
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №23
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №24
- •Теоретический материал
- •Примеры
- •Задания для самостоятельной работы
- •Практическое занятие №25
- •Теоретический материал
- •Примеры
- •2) Здесь ,,. Точка, изображающая число, лежит воIIчетверти;,. Значит,
- •Задания для самостоятельной работы
- •Список рекомендуемой литературы
Примеры
Задание 1:Найти
сумму и разность матриц и
и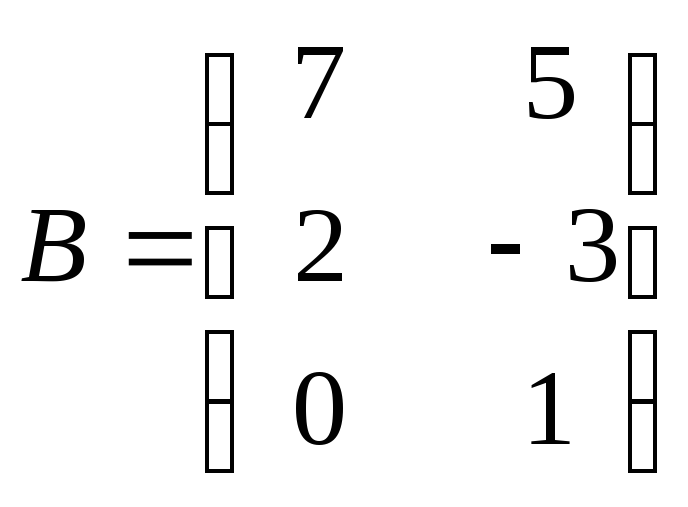 .
.
Решение:Здесь
даны матрицы одного размера![]() ,
следовательно, существуют их сумма и
разность. Согласно определению
алгебраической суммы матриц имеем
,
следовательно, существуют их сумма и
разность. Согласно определению
алгебраической суммы матриц имеем
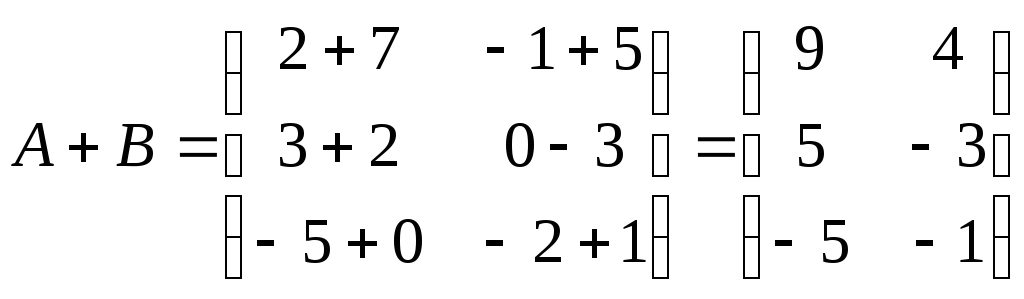 ,
,
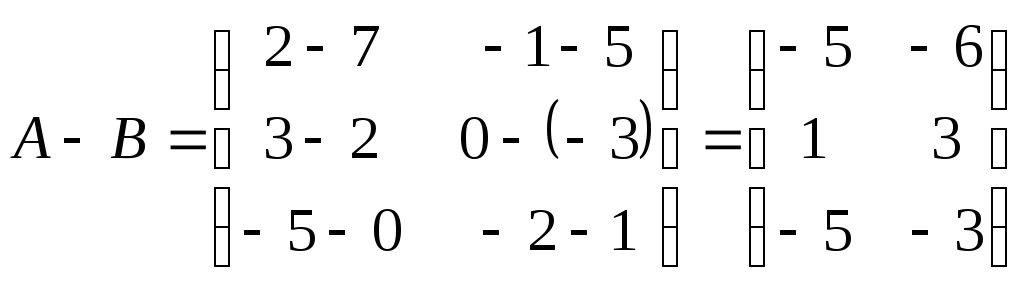 .
.
Задание
2:Вычислить определители: 1)![]() ; 2)
; 2) .
.
Решение:1)
По формуле (1) находим![]() .
.
2) Разлагая данный определитель, например, по элементам первой строки, находим
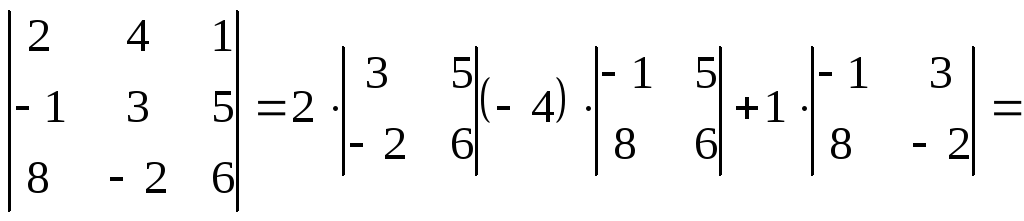
![]() .
.
Тот же результат получится, если воспользоваться формулой (2):
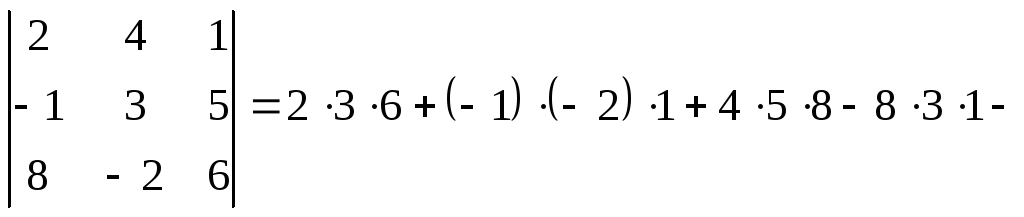
![]() .
.
Задания для самостоятельной работы
Найдите сумму матриц
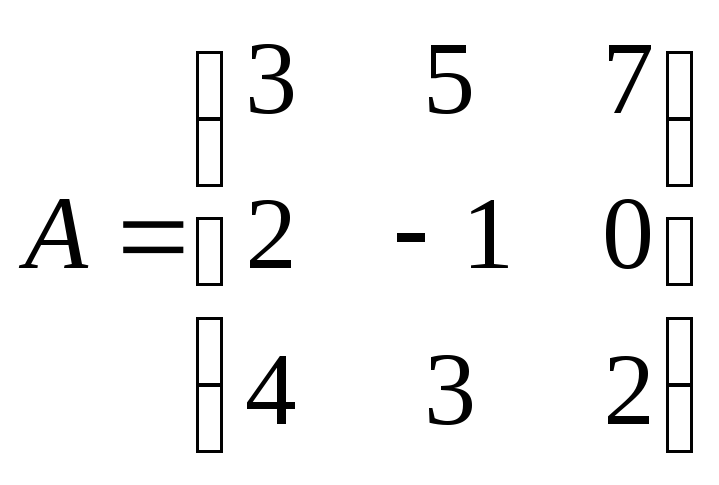 и
и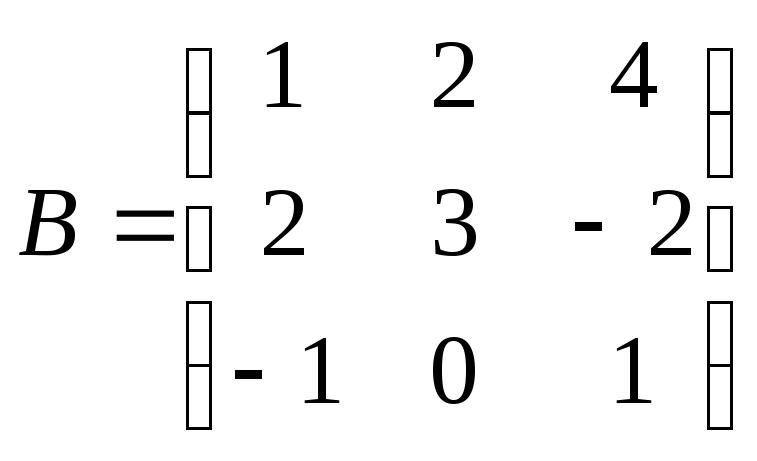 .
.Транспонируйте матрицу
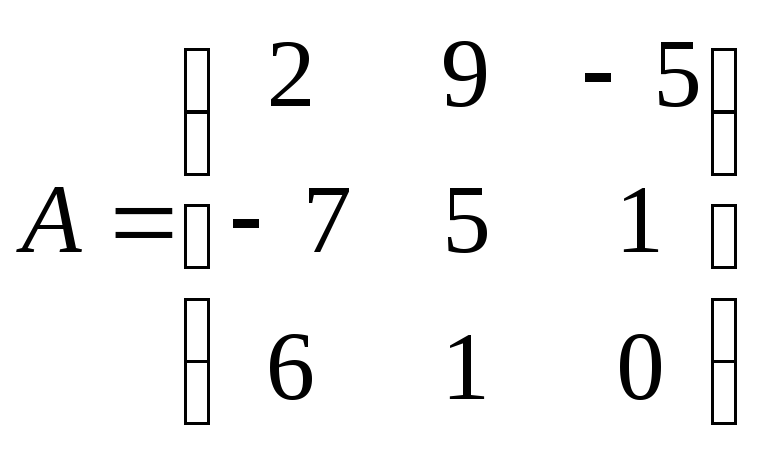 .
Укажите размеры данной и транспонированной
матриц.
.
Укажите размеры данной и транспонированной
матриц.Даны матрицы:
 ,
,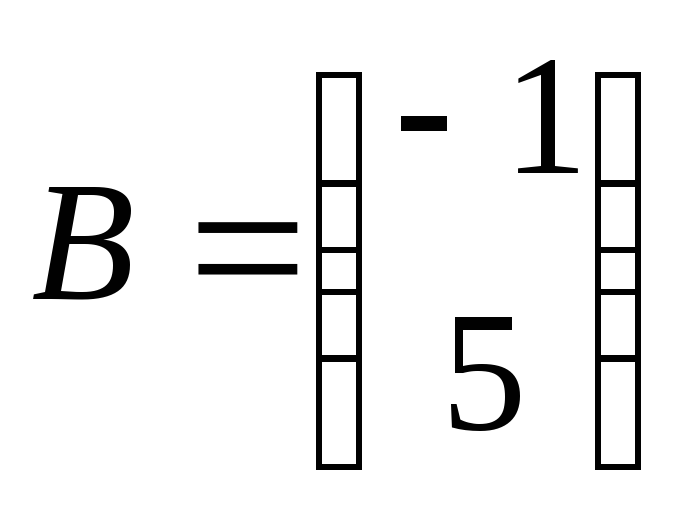 .
Произведите указанные действия, а в
случае, когда это невозможно, указать
причину: 1)
.
Произведите указанные действия, а в
случае, когда это невозможно, указать
причину: 1) ;
;
2)
![]() .
.
Даны матрицы
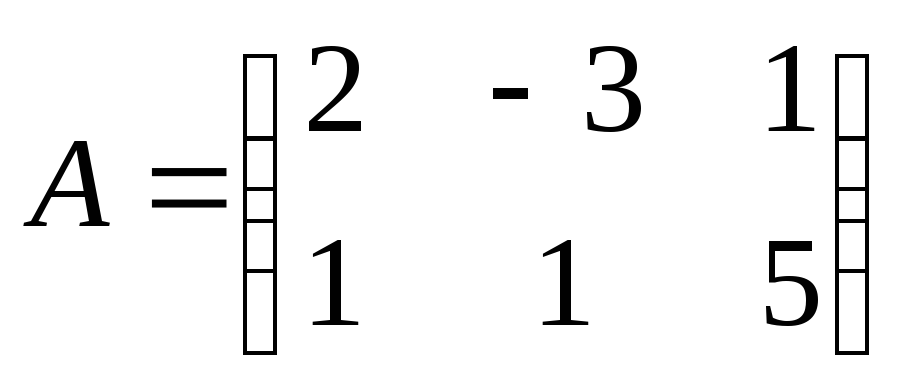 и
и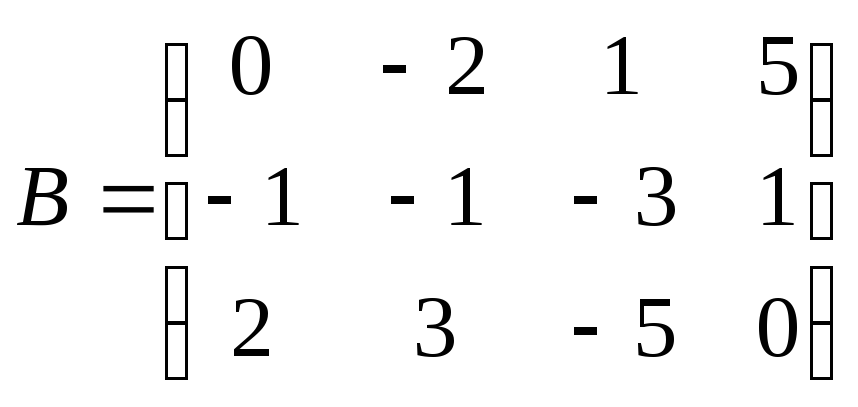 .
Найдите матрицу
.
Найдите матрицу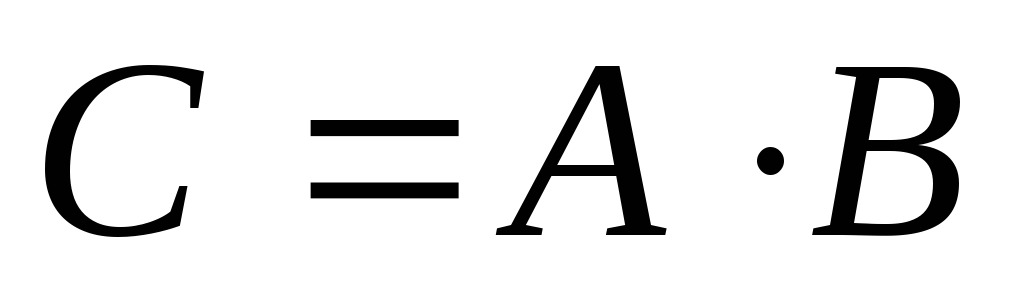 .
.Вычислите определители второго порядка: а)
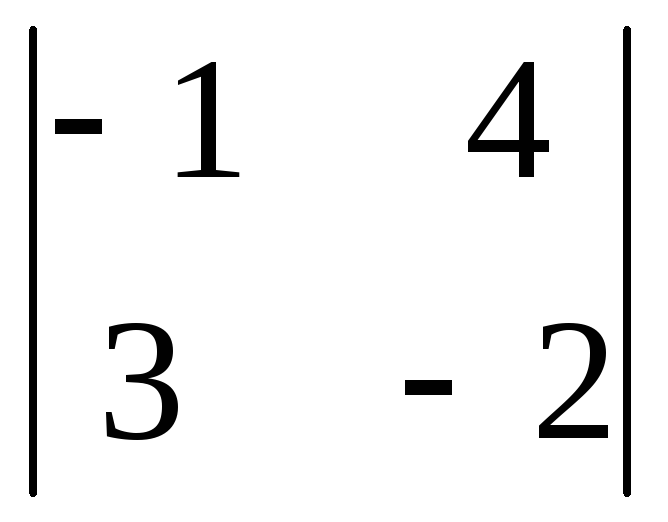 ;
;
б)
![]() .
.
Вычислите определители третьего порядка: а)
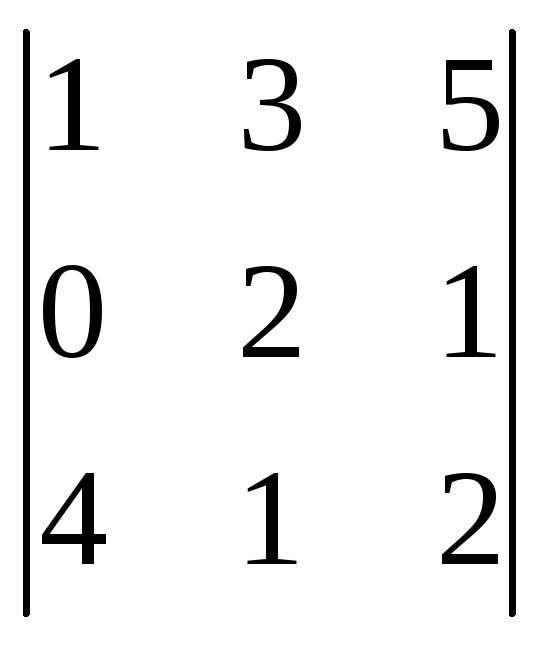 ;
;
б)
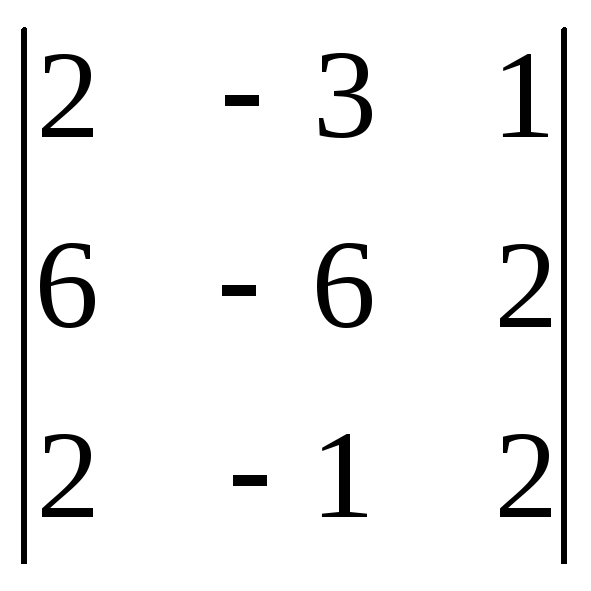 .
.
Вычислите определитель четвертого порядка
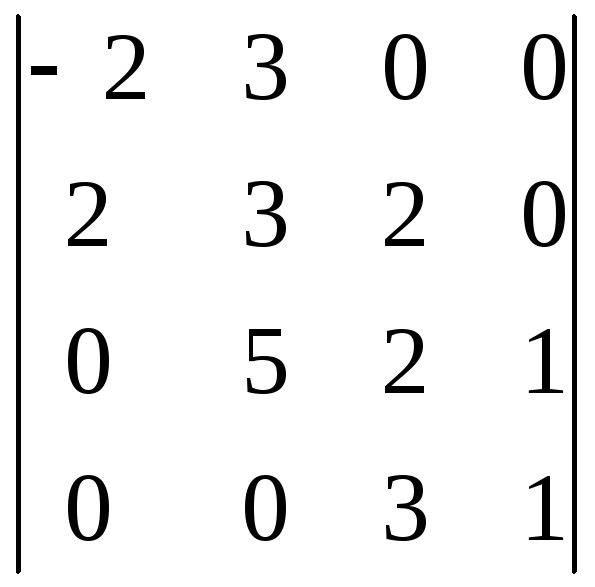 .
.
Вопросы для самоконтроля:
Что называется матрицей? Как установить размеры матрицы?
Назовите линейные операции над матрицами. Как они производятся?
Какие матрицы можно перемножать? Как это делается?
Что называется определителем? Как вычисляются определители второго и третьего порядков?
Что называется минором и алгебраическим дополнением для произвольного элемента
 определителя?
определителя?
Практическое занятие №2 Тема: Нахождение обратной матрицы
Цель: Формирование навыков нахождения обратной матрицы.
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Матрица,
состоящая из
![]() строк и
строк и![]() столбцов, называетсяквадратной
матрицей
порядка
столбцов, называетсяквадратной
матрицей
порядка
![]() :
:
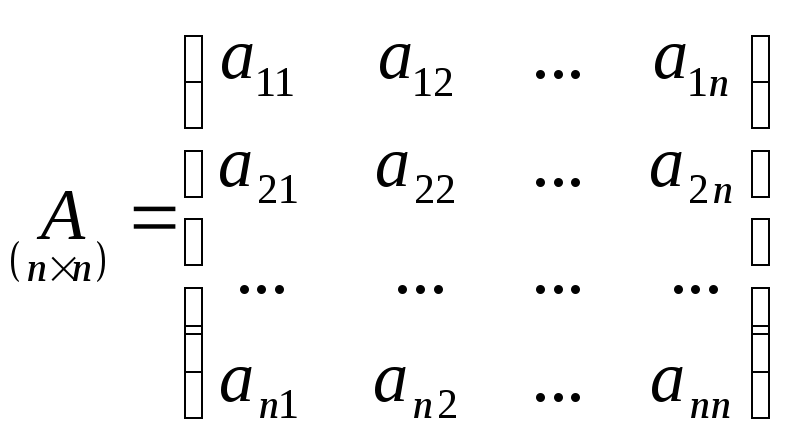 .
.
Элементы
![]() образуют главную диагональ матрицы.
образуют главную диагональ матрицы.
У
единичной
матрицы
![]() порядка
порядка![]() элементы главной диагонали равны
единицы, а остальные элементы равны
нулю:
элементы главной диагонали равны
единицы, а остальные элементы равны
нулю:![]() то есть
то есть
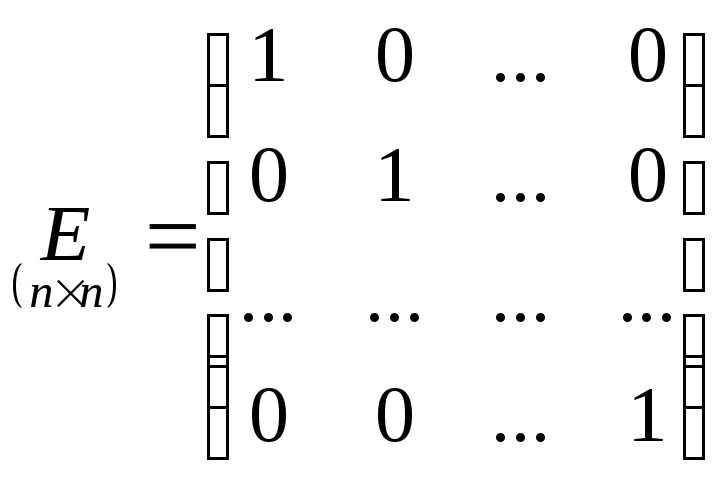 .
.
Для
![]() - матриц справедливы равенства
- матриц справедливы равенства![]() .
.
Каждой
![]() - матрице
- матрице![]() соответствует определитель
соответствует определитель![]() -го
порядка, который состоит из тех же
элементов, расположенных в том же
порядке, что и в матрице:
-го
порядка, который состоит из тех же
элементов, расположенных в том же
порядке, что и в матрице:
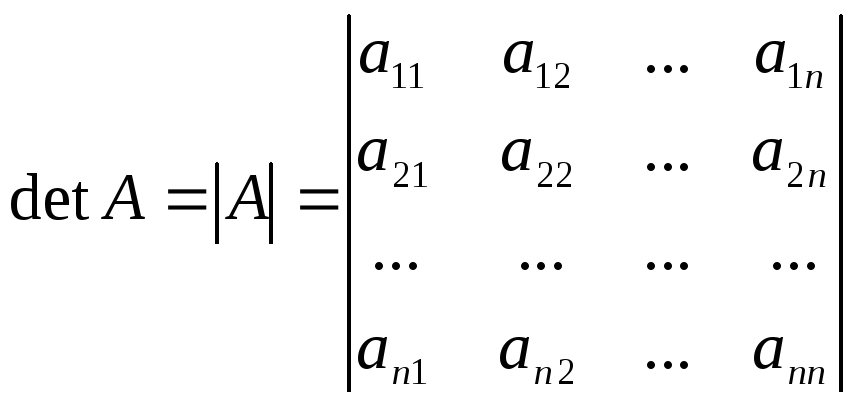 .
.
Произведение
двух квадратных матриц всегда определено;
при этом определитель
матрицы – произведения равен произведению
определителей матриц – сомножителей:
![]() .
.
Квадратная
матрица называется невырожденной,
если ее определитель отличен от нуля
![]() ,
ивырожденной
в противном случае
,
ивырожденной
в противном случае
![]() .
.
Всякая
невырожденная матрица
![]() порядка
порядка![]() имеетобратную
матрицу
того же порядка
имеетобратную
матрицу
того же порядка
![]() ,
удовлетворяющую соотношениям
,
удовлетворяющую соотношениям
![]() .
.
Обратная матрица имеет вид
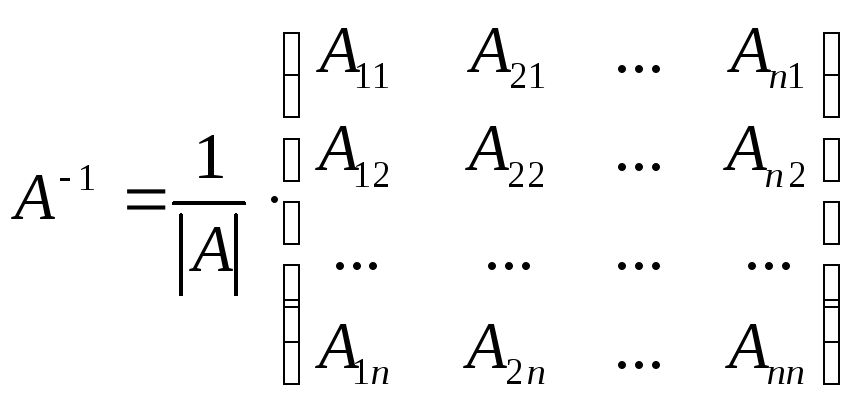 ,(1)
,(1)
где
![]() - алгебраическое дополнение элемента
- алгебраическое дополнение элемента![]() в определителе
в определителе![]() матрицы
матрицы![]() ,
то есть элементы обратной матрицы
находятся по формулам
,
то есть элементы обратной матрицы
находятся по формулам![]() .
.
Свойства обратной матрицы
(здесь
![]() - матрицы,
- матрицы,![]() - число)
- число)
 ;
;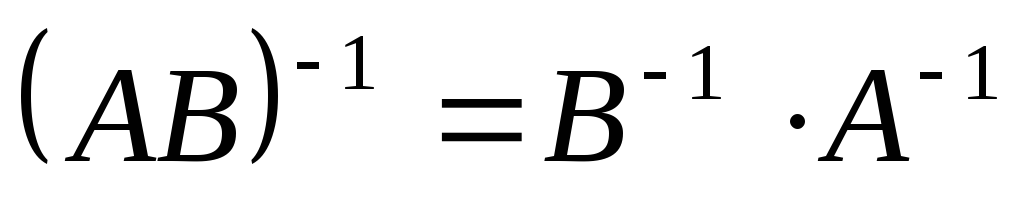 ;
;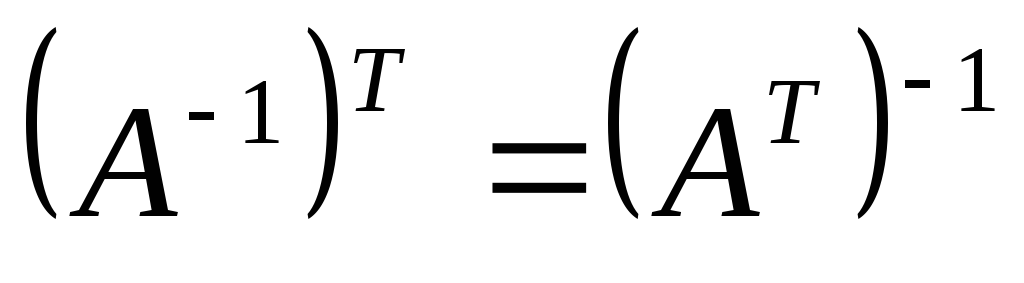 ;
;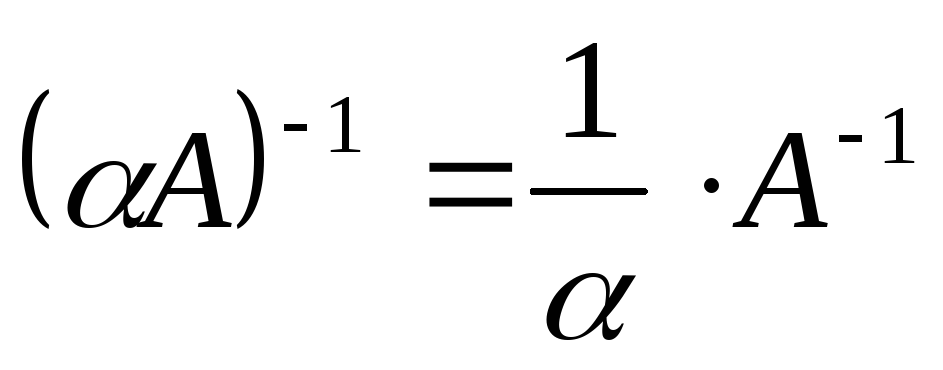 ;
; .
.
Пример
Задание: Для
матрицы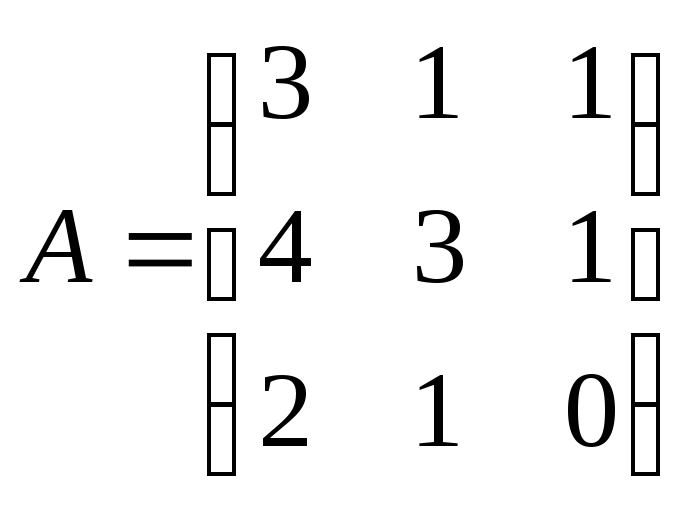 найти обратную
матрицу и проверить, что
найти обратную
матрицу и проверить, что
![]() .
.
Решение:Так
как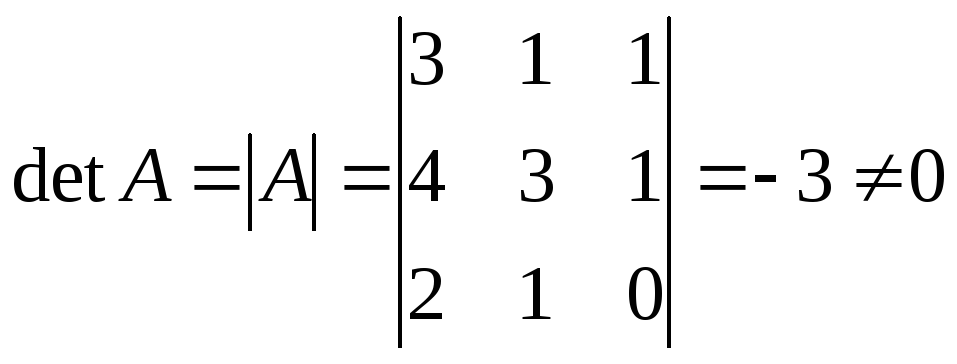 ,
томатрица
,
томатрица
![]() имеет обратную матрицу, элементы которой
равны
имеет обратную матрицу, элементы которой
равны![]() .
.
2)
Вычислим алгебраические дополнения
![]() элементов
элементов![]() для
для![]() :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Теперь, используя формулу (1), находим обратную матрицу
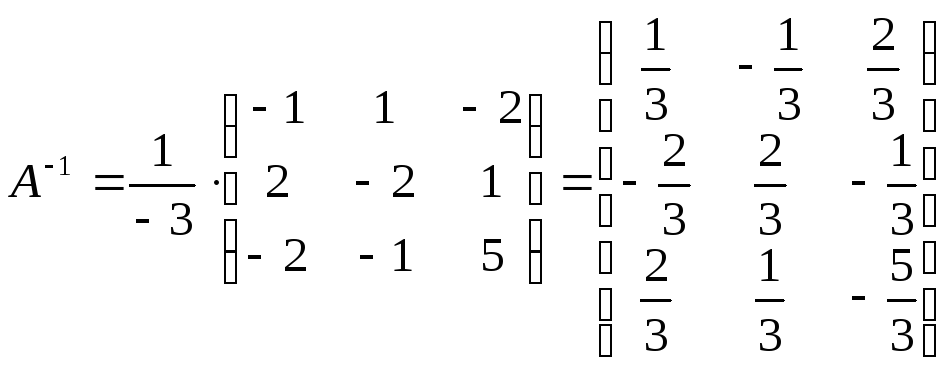 .
.
Далее вычислим произведение
 =
=
=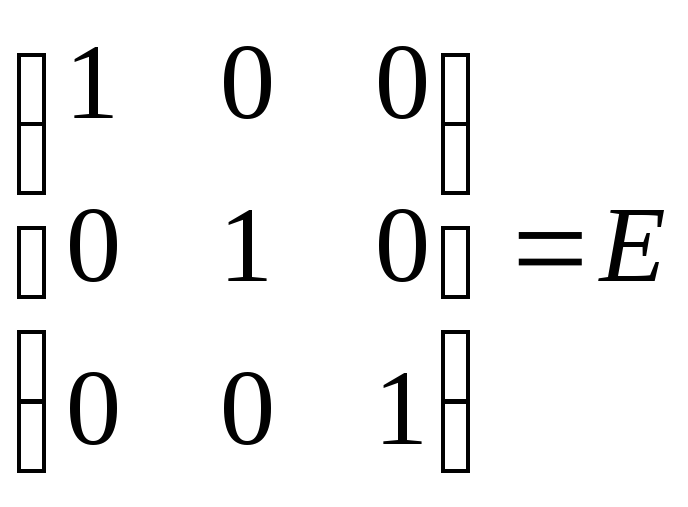 .
.
Аналогично находим
 .
Итак, обратная
матрица вычислена правильно.
.
Итак, обратная
матрица вычислена правильно.
Задания для самостоятельной работы
Для заданной матрицы
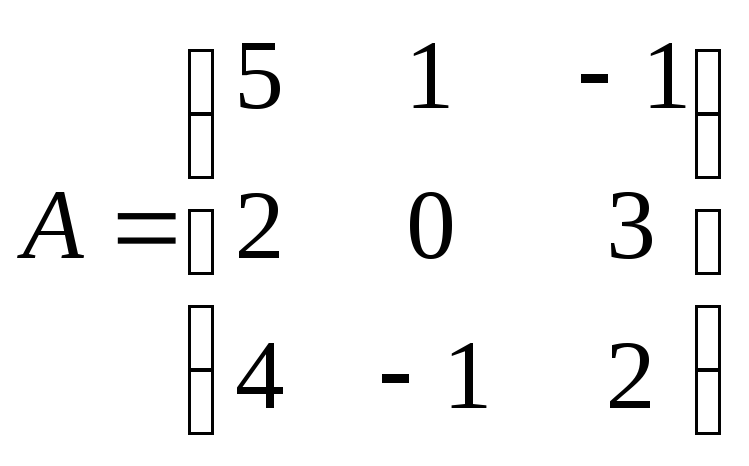 найти указанные элементы обратной
матрицы
найти указанные элементы обратной
матрицы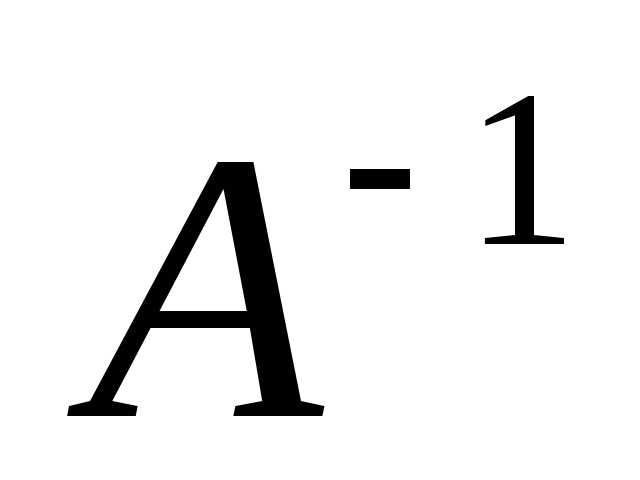 : 1)
: 1)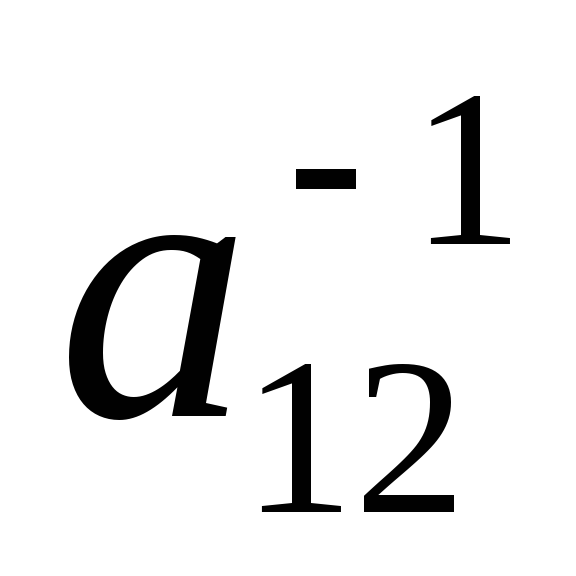 ; 2)
; 2)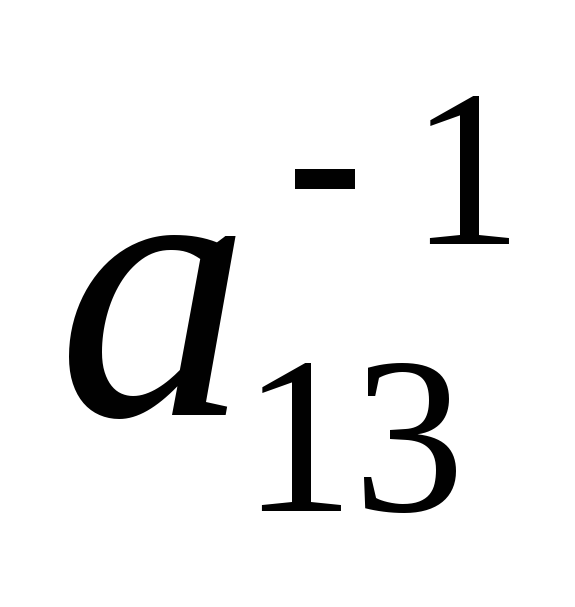 ; 3)
; 3)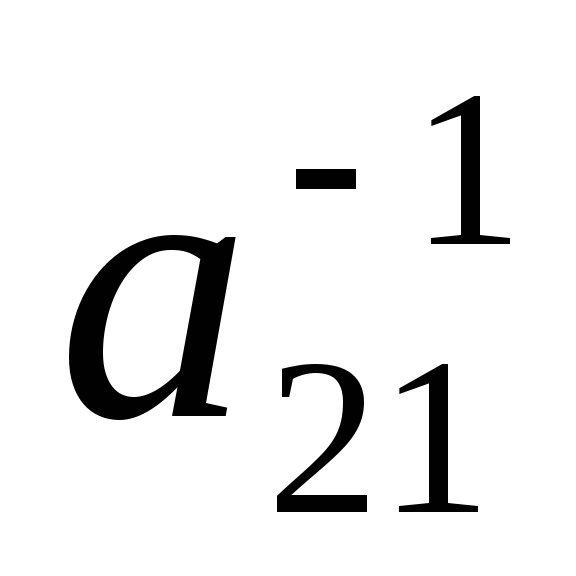 ;
;
4)
![]() ; 5)
; 5)![]() ; 6)
; 6)![]() .
.
Для матриц
 и
и найдите обратные матрицы,
найдите обратные матрицы,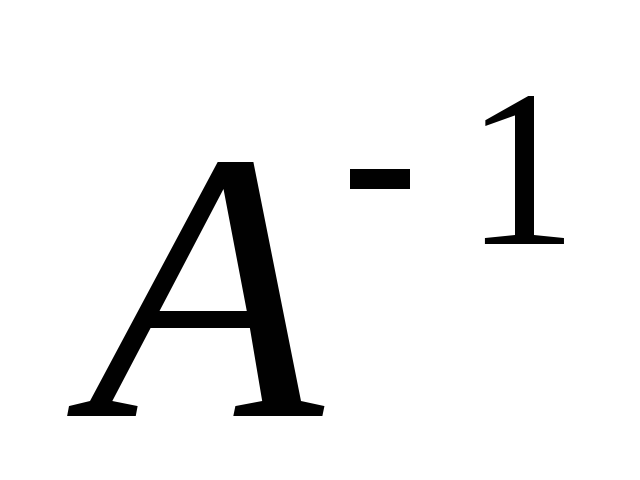 и
и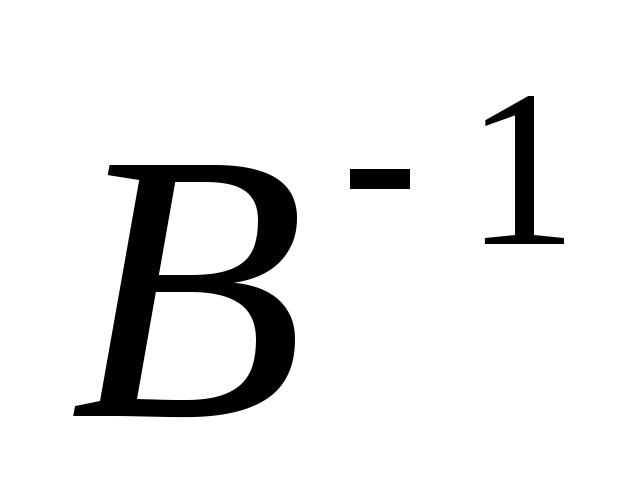 .
Проверить, верно, ли они найдены.
.
Проверить, верно, ли они найдены.
Вопросы для самоконтроля:
Какая матрица называется квадратной?
Какая матрица называется единичной, верхнетреугольной, нижнетреугольной, диагональной?
Дайте определение обратной матрицы. Всегда ли существует обратная матрица?
Как найти обратную матрицу?
Практическое занятие №3
Тема: Решение систем алгебраических уравнений по правилу Крамера и матричным методом
Цель: Формирование навыков решения СЛАУ по правилу Крамера и матричным методом.
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Пример
Задание:Показать, что система имеет единственное решение и найти его двумя способами: а) по правилу Крамера;
б) матричным методом.
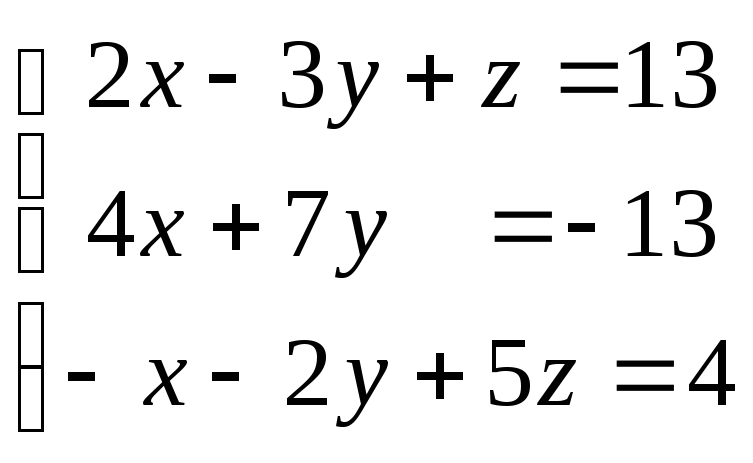
Решение:Данная
система имеет размер![]() (три уравнения и три неизвестных).
Составим матрицу
(три уравнения и три неизвестных).
Составим матрицу![]() из коэффициентов при неизвестных:
из коэффициентов при неизвестных:
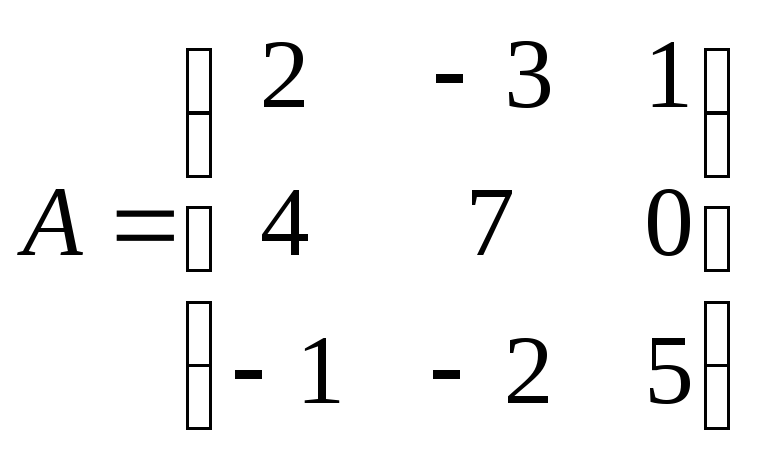 .
Матрица
.
Матрица
![]() квадратная
квадратная![]() .
Вычислим определитель матрицы
.
Вычислим определитель матрицы![]() ,
используя формулу его разложения по
элементам первой строки:
,
используя формулу его разложения по
элементам первой строки:
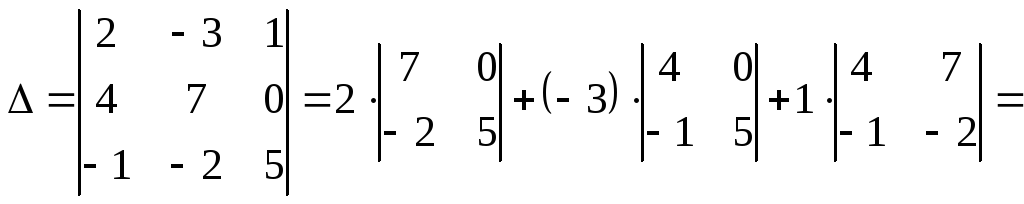
![]() .
.
Так как определитель
системы
![]() ,
то данная система имеет единственное
решение. Это решение можно найти по
правилу Крамера:
,
то данная система имеет единственное
решение. Это решение можно найти по
правилу Крамера:![]() ;
;![]() ;
;![]() ,
где
,
где![]() - главный определитель системы;
- главный определитель системы;![]() ,
,![]() ,
,![]() - вспомогательные определители, которые
получаются из главного путем замены
соответствующего столбца на столбец
свободных членов, и вычисляются аналогично
определителю
- вспомогательные определители, которые
получаются из главного путем замены
соответствующего столбца на столбец
свободных членов, и вычисляются аналогично
определителю![]() .
.
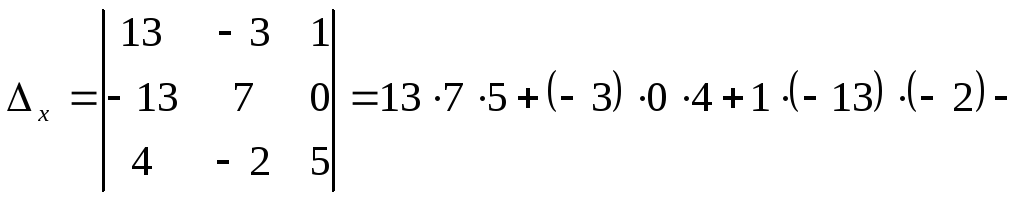
![]() ;
;
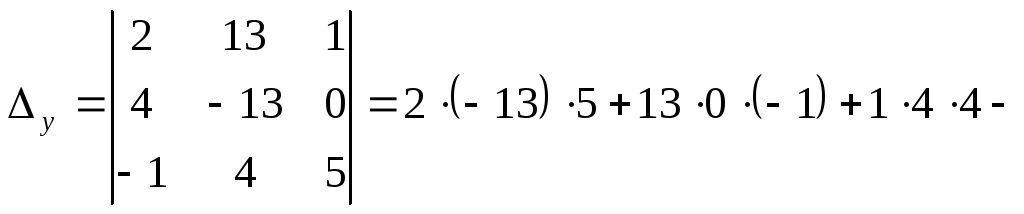
![]() ;
;
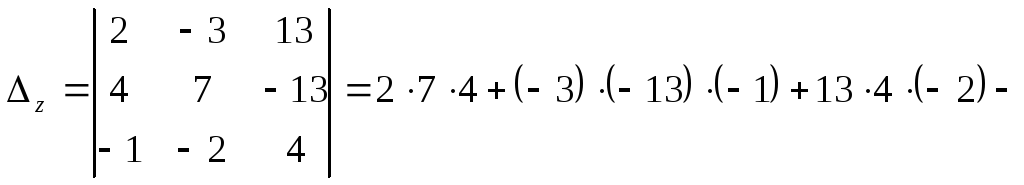
![]()
Отсюда по правилу Крамера имеем:
![]() ;
; ![]() ;
;
![]() .
.
Решение системы
единственно, это совокупность чисел
![]() .
.
Проверка:Подставим найденное решение во все уравнения исходной системы линейных алгебраических уравнений.
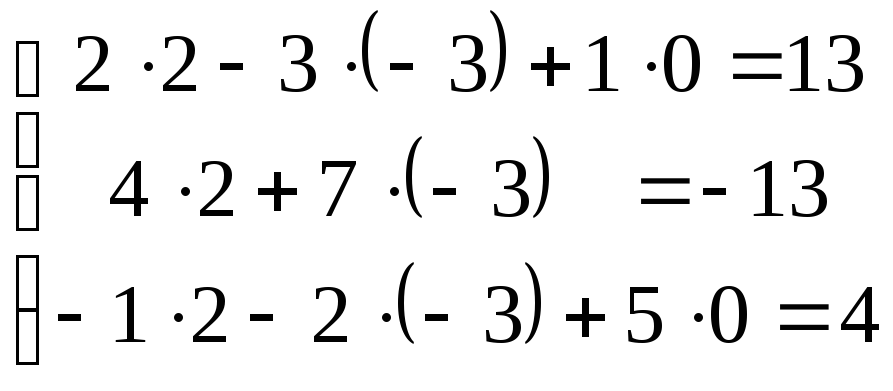
![]()
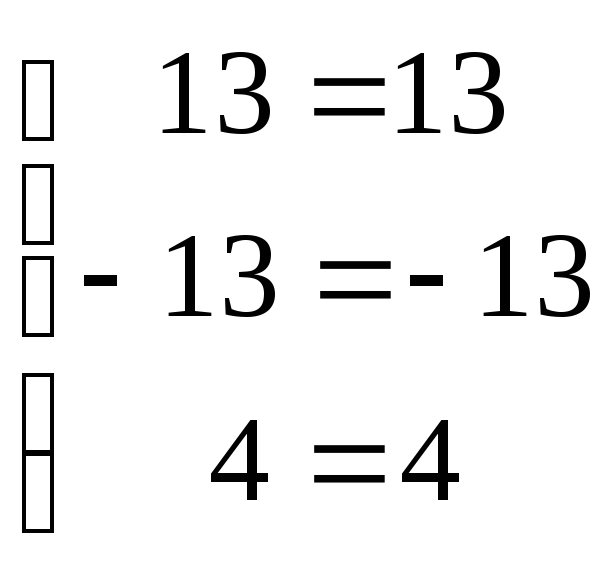
Так как все уравнения системы обратились в равенства, то решение найдено верно.
Ответ:![]() .
.
Решим данную систему матричным способом. Рассмотрим матрицы:
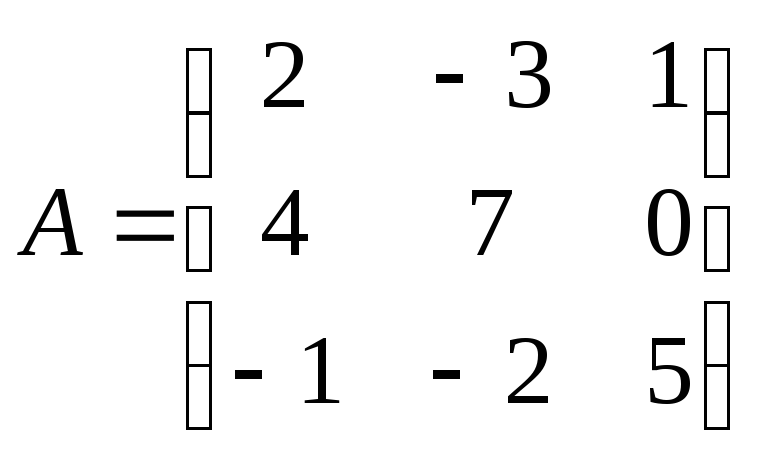 ;
; 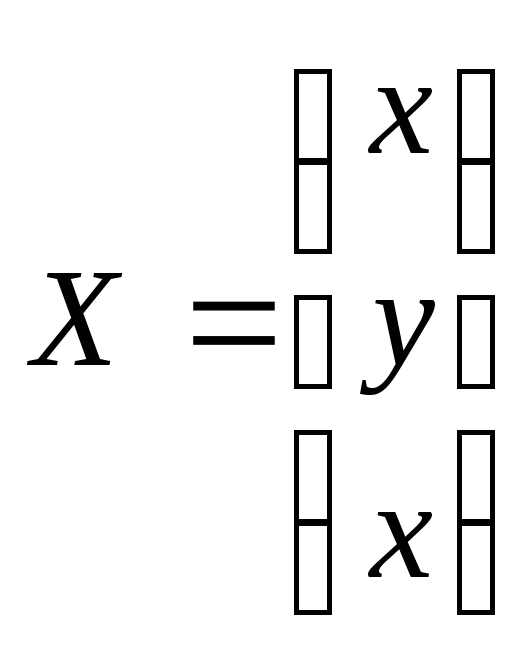 ;
; ;
;
![]() - матрица коэффициентов
при неизвестных,
- матрица коэффициентов
при неизвестных,
![]() - матрица – столбец неизвестных,
- матрица – столбец неизвестных,![]() - матрица – столбец свободных членов.
- матрица – столбец свободных членов.
Данную систему можно записать в виде:

![]()
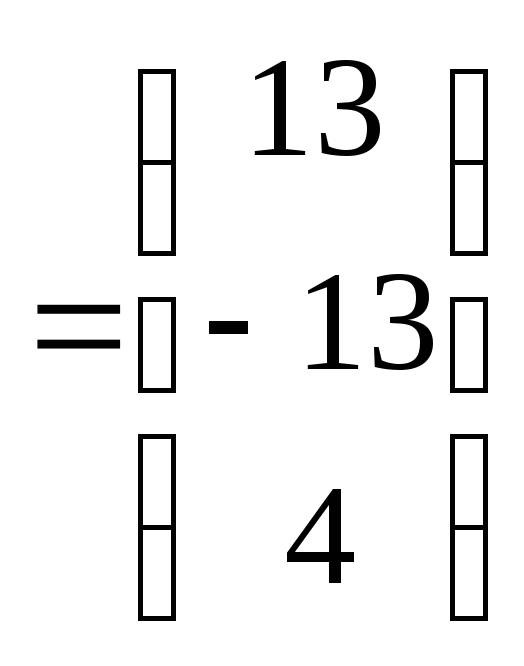 ;
;
При умножении
матриц каждая строка матрицы
![]() умножается на столбец матрицы
умножается на столбец матрицы![]() и в результате получается соответствующий
элемент матрицы
и в результате получается соответствующий
элемент матрицы![]() .
Таким образом, последняя матричная
запись содержит все три уравнения данной
системы линейных алгебраических
уравнений. Коротко ее можно записать
так:
.
Таким образом, последняя матричная
запись содержит все три уравнения данной
системы линейных алгебраических
уравнений. Коротко ее можно записать
так:
![]() (1)
(1)
Рассмотрим матрицу
![]() ,
обратную к матрице
,
обратную к матрице![]() .
Это такая матрица, которая при умножении
на данную матрицу
.
Это такая матрица, которая при умножении
на данную матрицу![]() дает единичную матрицу
дает единичную матрицу![]() :
:![]() ,
где
,
где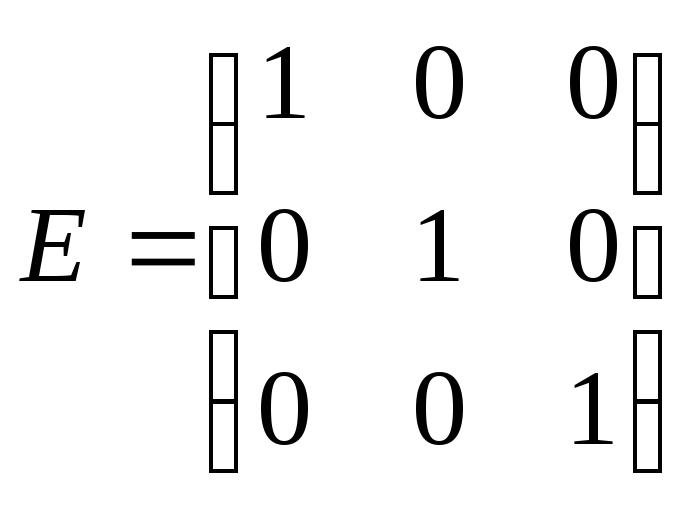 .
.
Умножая обе части
матричного равенства (2) на матрицу
![]() слева, получим:
слева, получим:
![]() ,
,
![]()
 ,
и окончательно имеем:
,
и окончательно имеем:
![]() (2)
(2)
Формула (2)
используется для нахождения решения
системы линейных алгебраических
уравнений. Предварительно нужно вычислить
обратную матрицу. Обратная матрица
вычисляется по формуле:
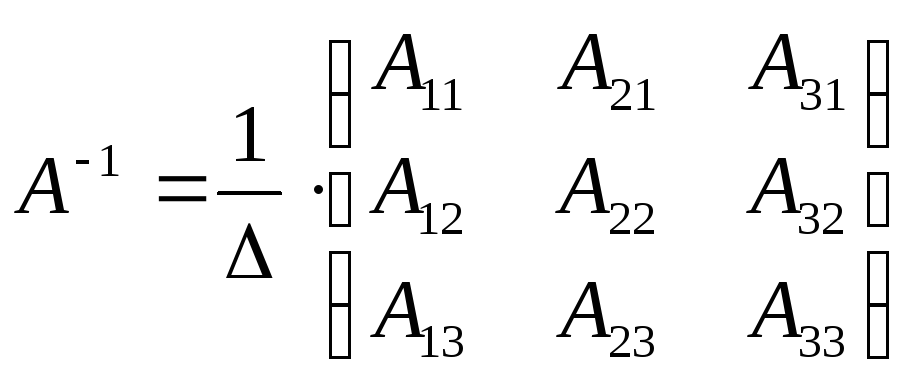 (3),
где
(3),
где![]() - алгебраическое дополнение всех
элементов матрицы
- алгебраическое дополнение всех
элементов матрицы![]() ,
,
![]() - главный определитель
системы
- главный определитель
системы
![]() .
.
В нашем примере
![]() .
.
Найдем теперь
алгебраические дополнения для всех
элементов матрицы
![]() :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Составим матрицу алгебраических дополнений:
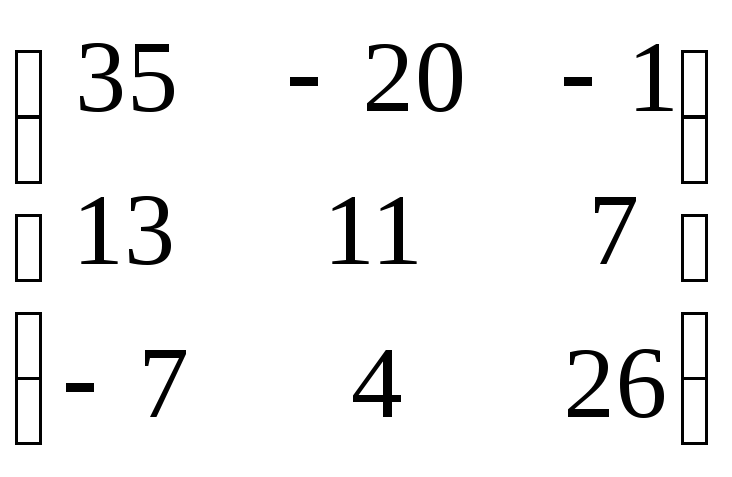 .
.
Транспонируем ее, то есть поменяем местами столбцы и строки с одинаковыми номерами:
 .
.
Обратную матрицу
получим по формуле (3), умножая каждый
элемент последней матрицы на число,
равное
![]() :
:
 .
.
Решение системы
линейных алгебраических уравнений
находим по формуле (2) умножением матрицы
![]() на матрицу свободных членов
на матрицу свободных членов![]() :
:
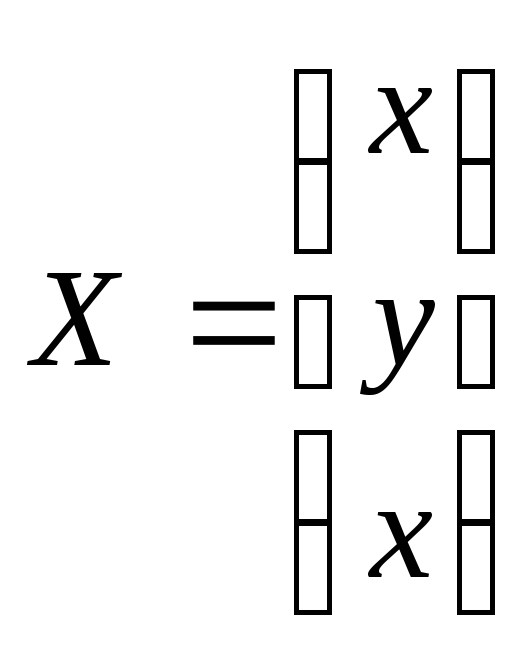 =
=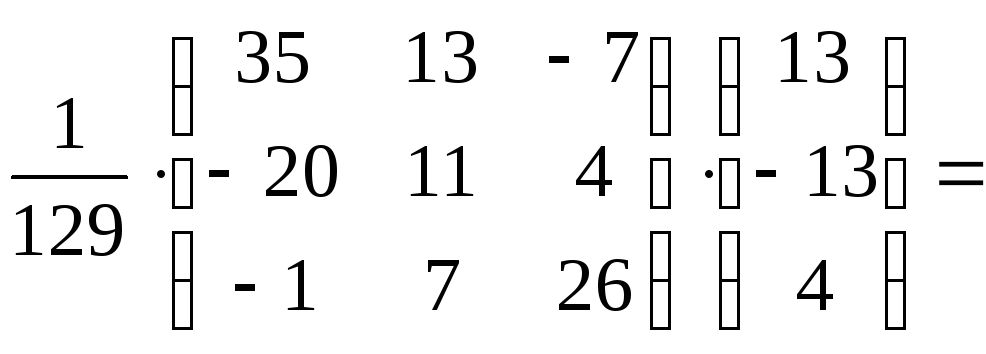
 Отсюда
следует, что
Отсюда
следует, что
![]() ,
,![]() ,
,![]() .
.
Найденное решение
![]() было проверено выше, и совпадает с
результатом, полученным по правилу
Крамера.
было проверено выше, и совпадает с
результатом, полученным по правилу
Крамера.
Ответ:![]() - единственное решение системы.
- единственное решение системы.
