Примеры

Задание:Вычислить площади фигур, ограниченных указанными линиями:

1) ,,и;

2) ,,и.

Решение:1) Строим прямуюпо двум точками.

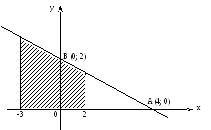
Выразим через, получим. Найдем площадь полученной фигуры:

Ответ:

2)- квадратичная функция;; график – парабола, ветви направлены вверх. Найдем координаты вершины параболы:, отсюда следует, что. Таким образом, вершина параболы имеет координаты:. Найдем площадь полученной фигуры:

.

Ответ:

Задания для самостоятельной работы

1. Найти площадь фигуры, ограниченной прямыми ,,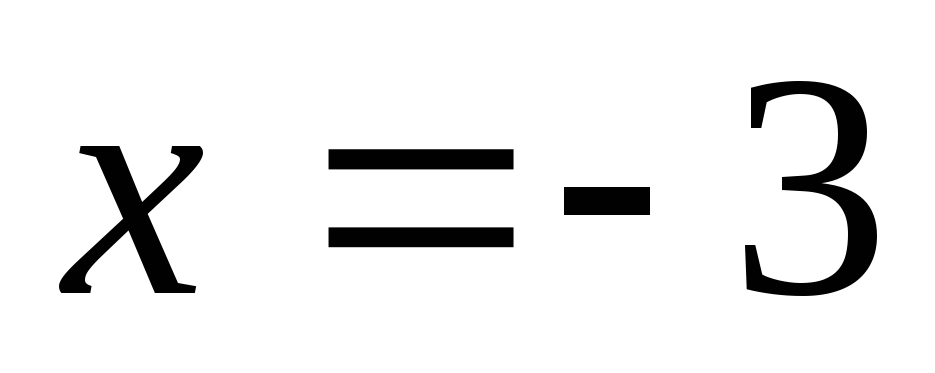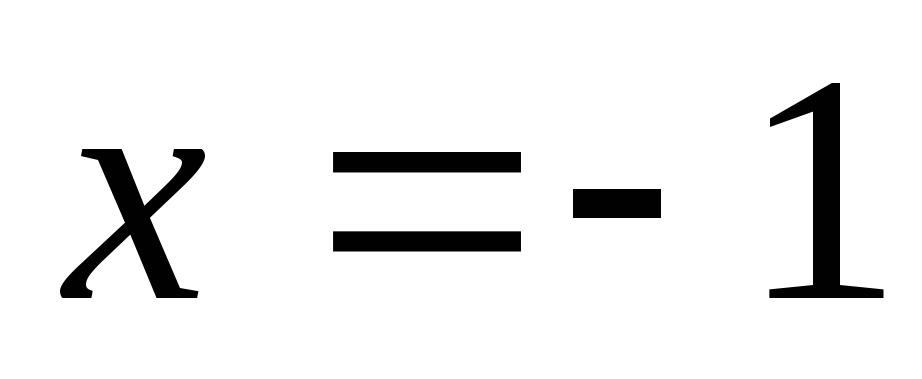и осью абсцисс.

2. Найти площадь фигуры, заключенной между осями координат и прямыми 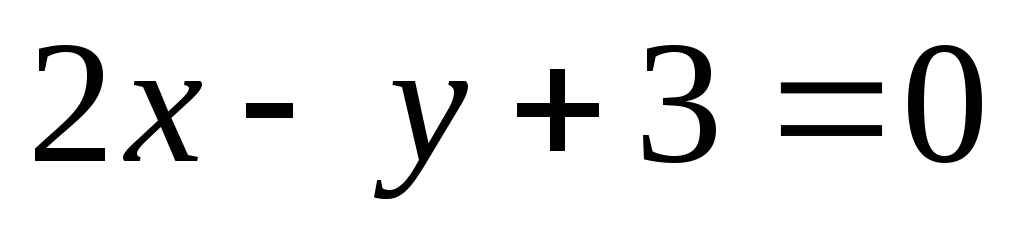и.

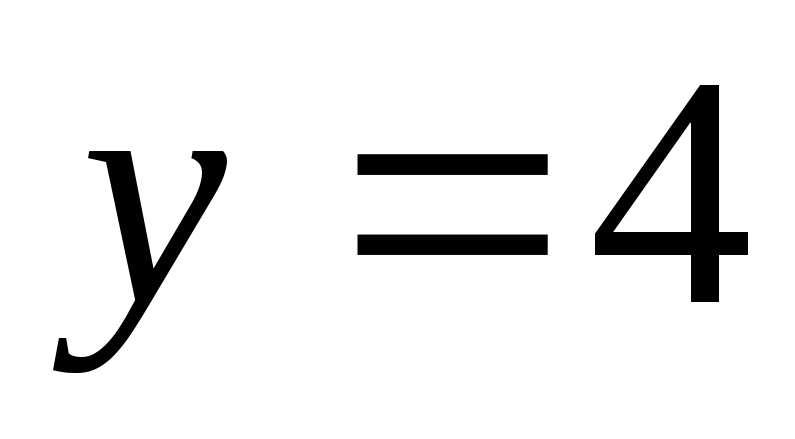3. Найти площадь фигуры, ограниченной ветвью гиперболы 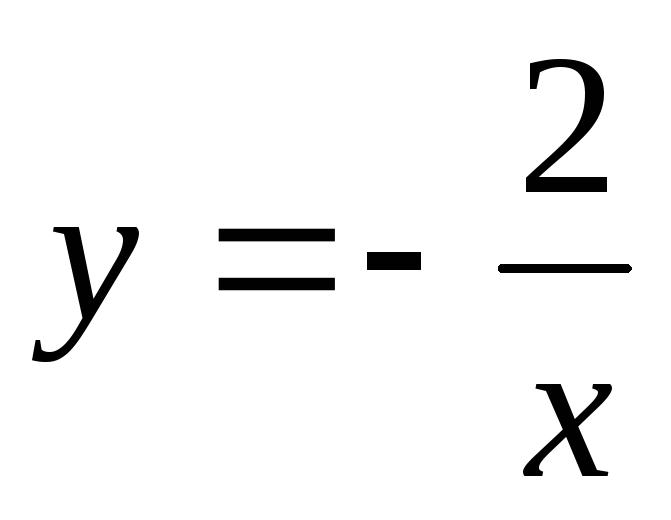и прямыми,.

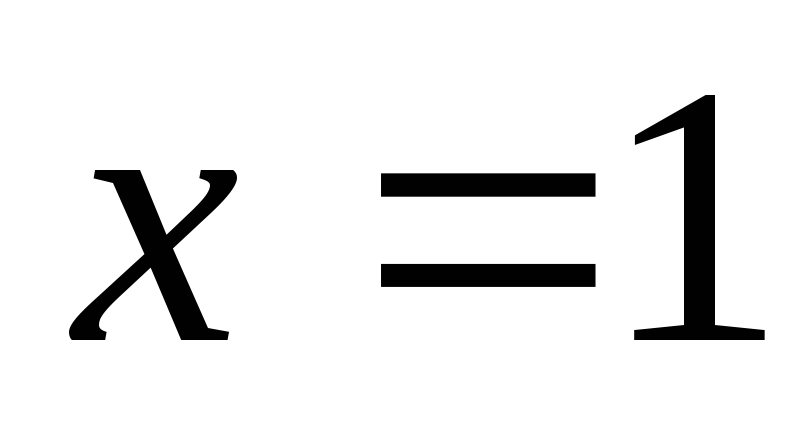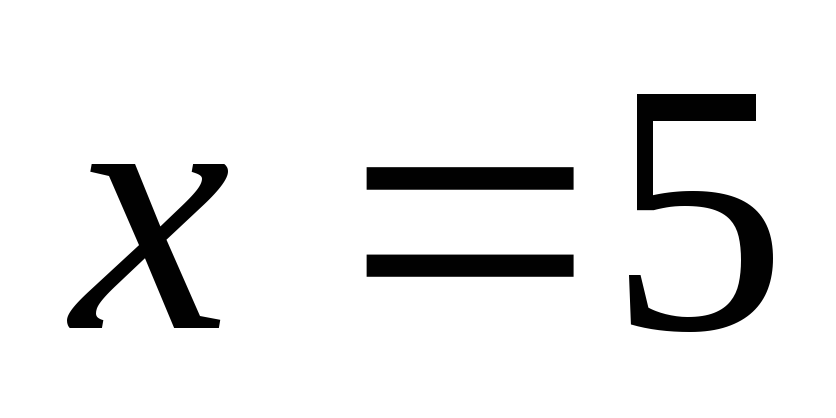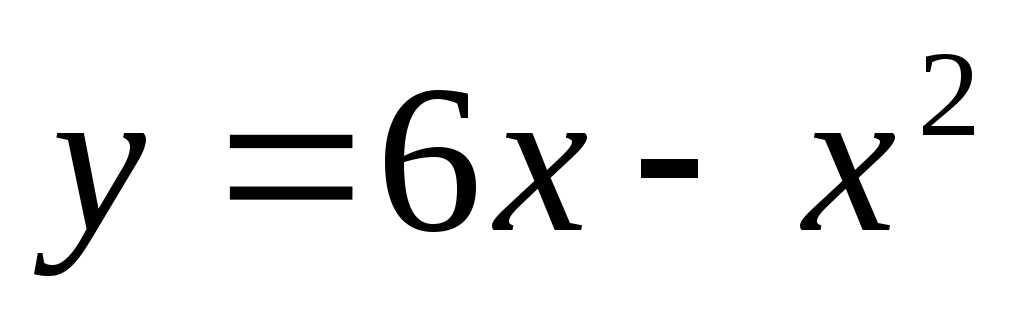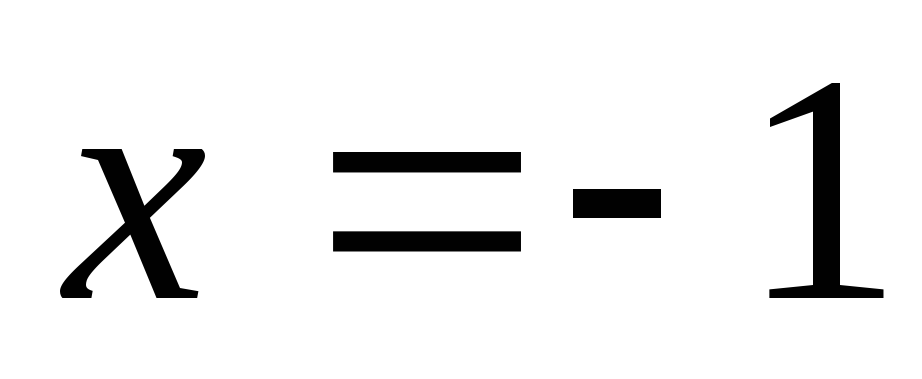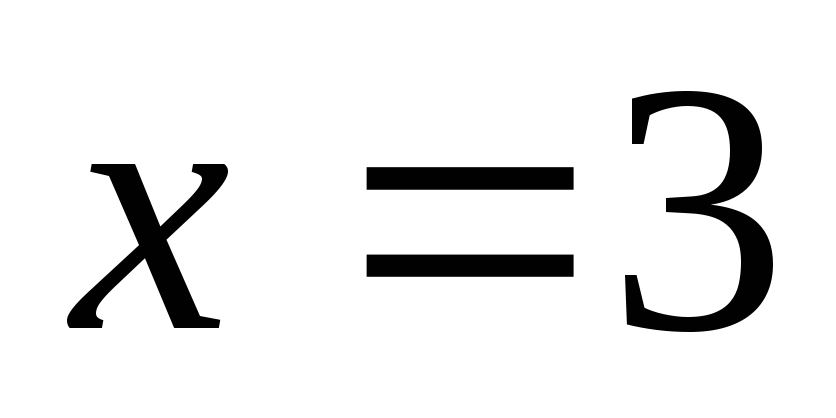4. Вычислить площадь фигуры, ограниченной параболой , прямыми,и осью абсцисс.

5. Найти площадь фигуры, ограниченной параболой , осями координат и прямой.

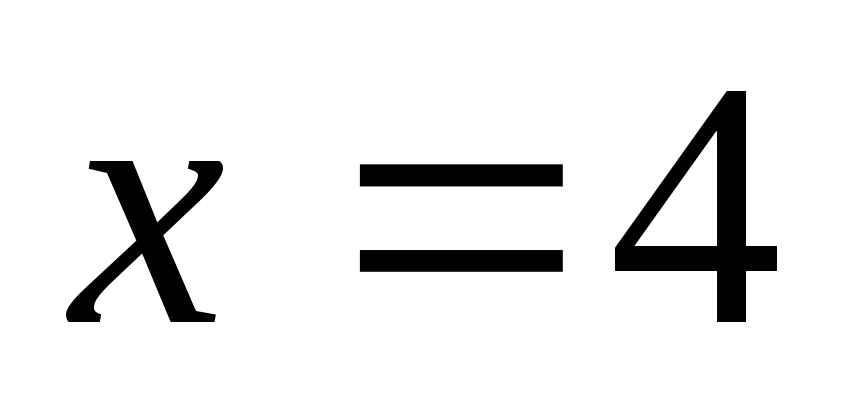6. Найти площадь фигуры, заключенной между прямыми 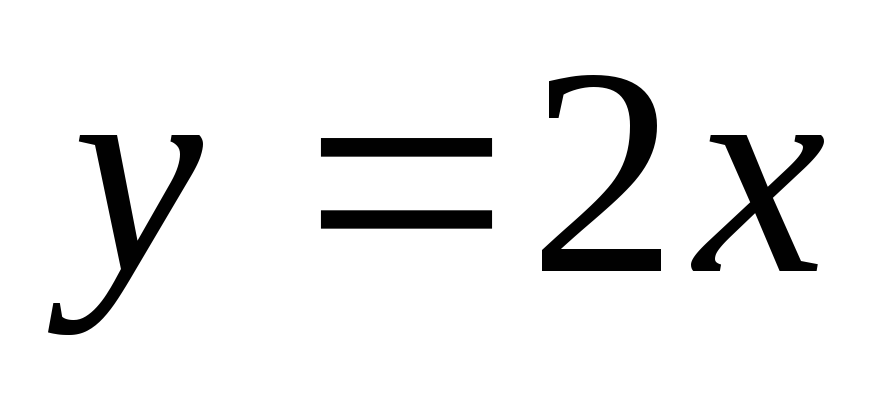,,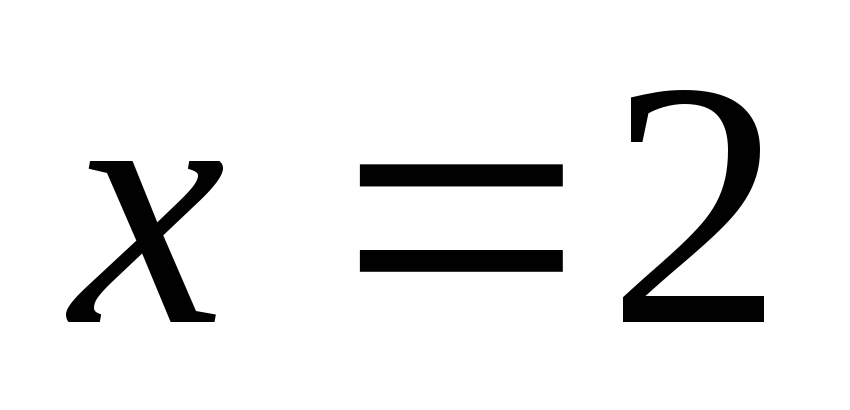и.

7. Найти площадь фигуры, отсекаемой от параболы 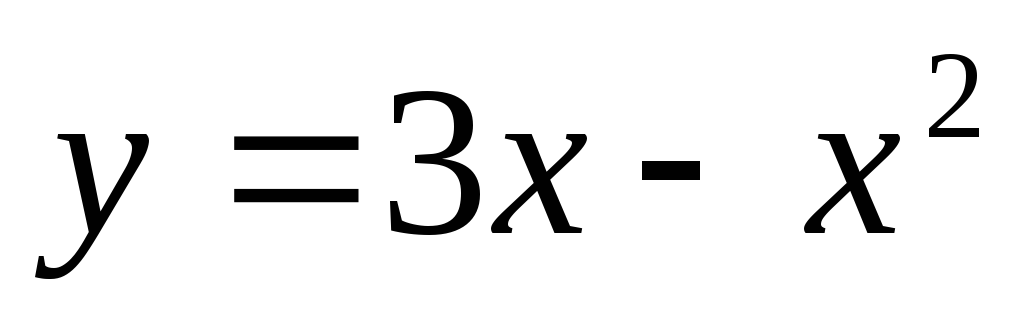прямой.

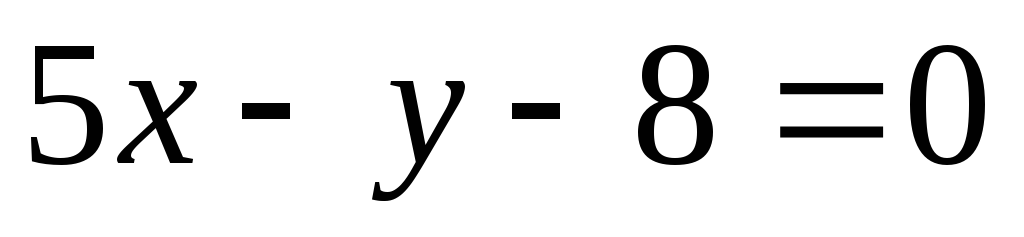8. Вычислить площадь фигуры, ограниченной параболой 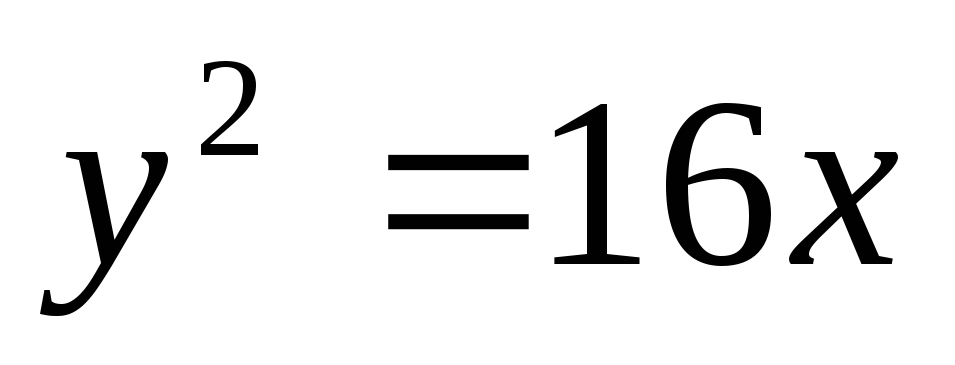и прямой.

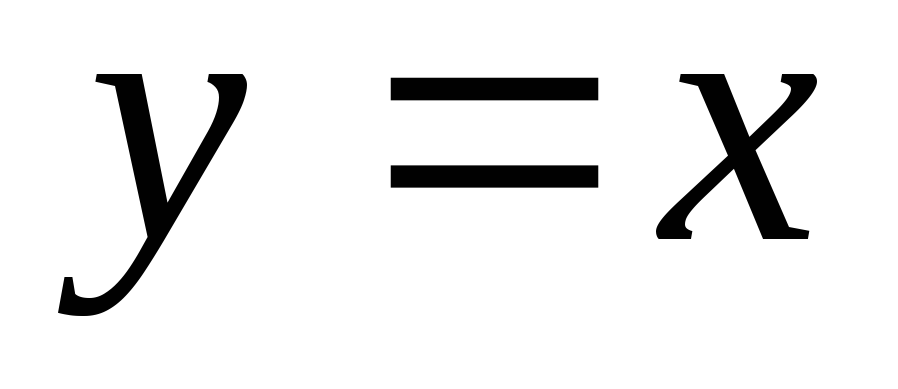9. Найти площадь фигуры, заключенной между параболами 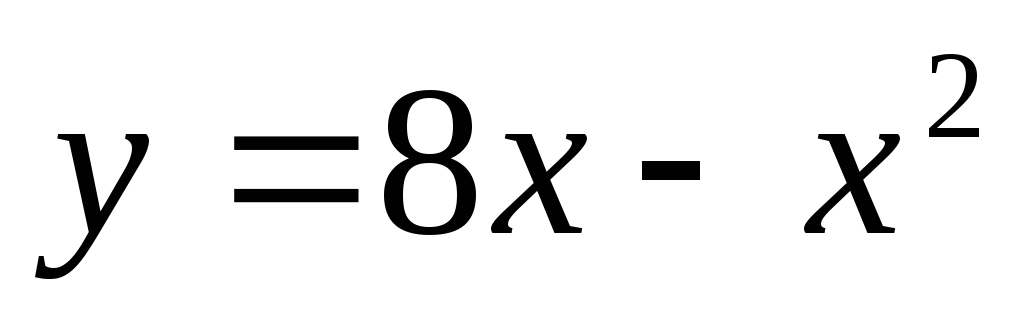и.

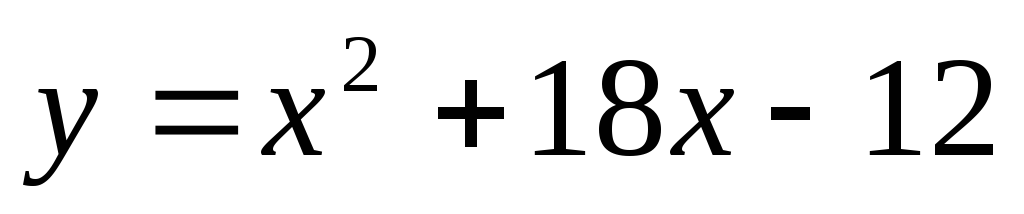10. Вычислить площадь фигуры, заключенной между кривым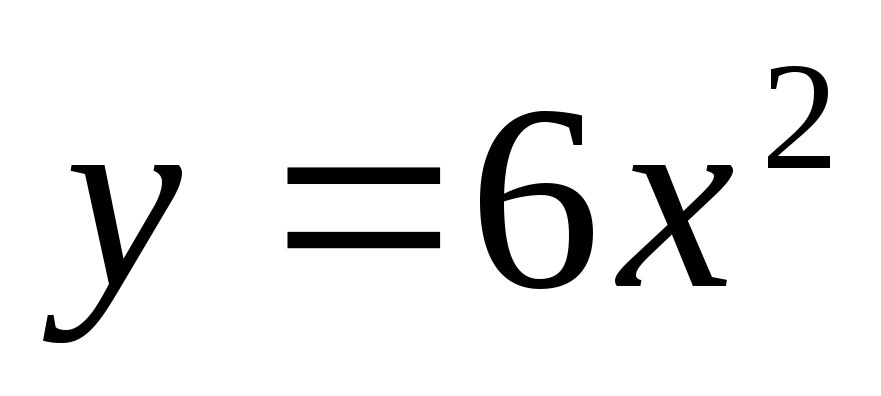и и.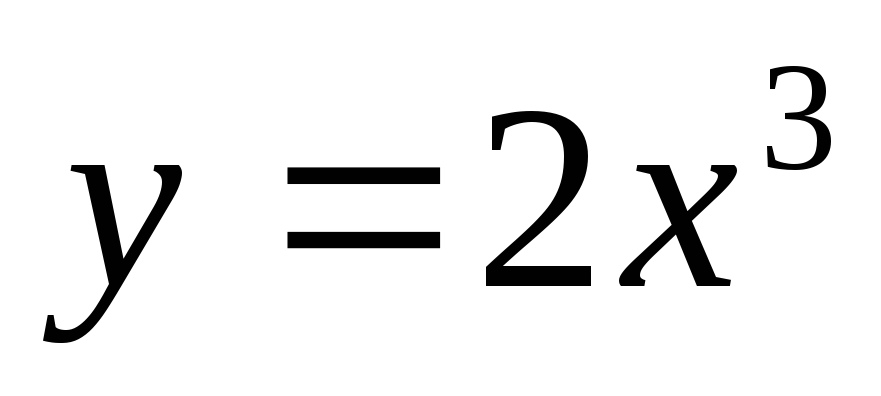

Вопросы для самоконтроля:

1. По какой формуле вычисляется площадь фигуры, находящейся над осью ?

2. По какой формуле вычисляется площадь фигуры прилегающей к оси ?

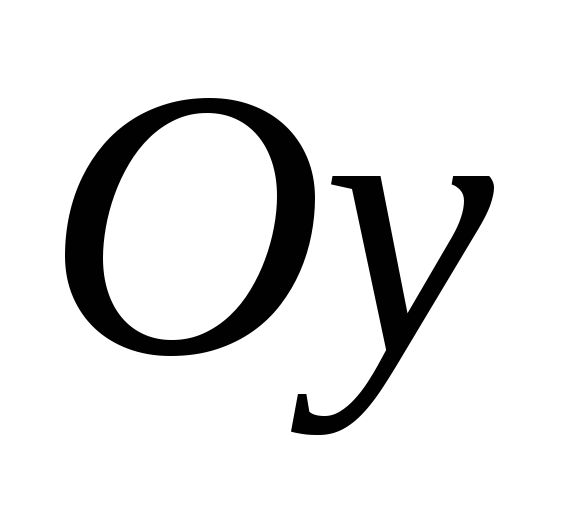3. По какой формуле вычисляется площадь фигуры, находящейся под осью ?

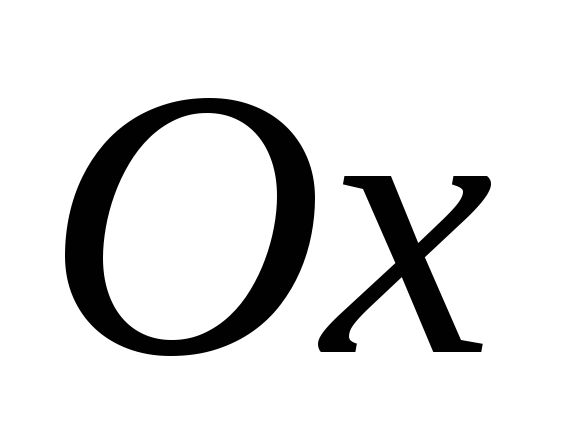4. По какой формуле вычисляется площадь фигуры расположенной по обе стороны оси ?

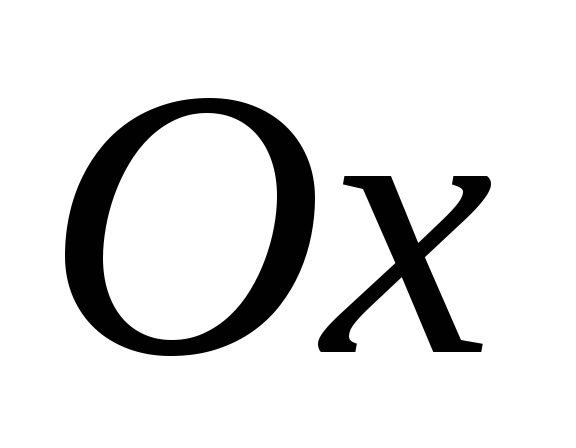5. По какой формуле вычисляется площадь фигуры,ограниченной двумя пересекающимися кривыми?

Практическое занятие №16

Тема: Нахождение области определения и вычисление частных значений для функции нескольких переменных

Цель: Формирование навыков нахождения области определения и вычисления частных значений для функции нескольких переменных

На выполнение практической работы отводится 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы

2.Оформить задания в тетради для практических работ

Теоретический материал

Уравнение

(неявная форма) (1)

или

(явная форма) (2)

определяет переменную какфункцию независимых переменных.Областью определения функции переменныхявляется множество точек-мерного пространства, в которых функция принимает определенное действительное значение.

При уравнение (1) определяет функцию трех переменных

или ,

Областью определения которой является множество точек трехмерного пространства.

При уравнение (1) определяет функцию двух переменных

или .

Частным значениемфункцииназывается такое ее значение, которое соответствует системе значений.

Примеры

Задание 1:Найти области определения функций:

1) ; 2).

Решение:1) Область определения функции состоит из всех точекплоскости, для которых, то есть. Таким образом, искомая область есть круг с центром в начале координат и радиусом 1. она является замкнутой, так как включает свою границу – окружность.

2) Так как логарифм определен только при положительных значениях аргумента, то , откуда. Следовательно, областью определения данной функции служит внутренняя часть круга с центром в начале координат и радиусом 3. эта область открытая, поскольку она не включает свою границу – окружность.

Задание 2:Найти частное значение функциив точке.

Решение:Подставляя в выражение функции значенияи, получим.