Практическое занятие №10

Тема: Вычисление производных сложных функций

Цель: Формирование навыков вычисления производных сложных функций

На выполнение практической работы отводится 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы

2.Оформить задания в тетради для практических работ

Теоретический материал

Пусть и- дифференцируемые функции. Тогда сложная функцияесть также дифференцируемая функция, причем

, или (1)

Это правило распространяется на цепочку из любого количества дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.

Пример

Задание:Найдите производные функций: 1);

2) .

Решение:1) Предположим, что, где. Тогда по формуле (1) найдем

.

2) Предполагая, что ,,, получим

.

Задания для самостоятельной работы

Вычислить производные заданных функций:

1) ; 2); 3);

4) ; 5); 6);

7) ; 8); 9);

10) ; 11); 12).

Вопросы для самоконтроля:

1. Дайте определение производной функции.

2. Перечислите правила нахождения производной функции.

3. Какие функции называются дифференцируемыми?

4. Какая функция называется сложной?

5. Как найти производную сложной функции?

Практическое занятие №11

Тема: Вычисление производных и дифференциалов высших порядков

Цель: Формирование навыков вычисления производных и дифференциалов высших порядков

На выполнение практической работы отводится 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы

2.Оформить задания в тетради для практических работ

Теоретический материал

Производная второго порядка(вторая производная) от функцииесть производная от ее первой производной:.

Производная третьего порядка(третья производная) от функцииесть производная от ее второй производной:.

Производная n – го порядка(n – япроизводная) от функцииесть производная от ее(n – 1) – ойпроизводной:.

Дифференциал второго порядка(второй дифференциал) функцииесть дифференциал от ее первого дифференциала:.

Дифференциалтретьего порядка(третий дифференциал) функцииесть дифференциал от ее второго дифференциала:.

Дифференциал n – го порядка(n – ыйдифференциал) функцииесть дифференциал от ее(n – 1) – огодифференциала:.

Примеры

Задание 1:Найти,,, …, если.

Решение:,

,

,

,,.

Задание 2:Найти дифференциалы первого, второго и третьего порядков функции.

Решение:,

,

.

Задания для самостоятельной работы

1. Найти производные второго порядка:

1) ; 2);

3) ; 4);

5) ; 6);

7) ; 8);

9) .

2. Дана функция 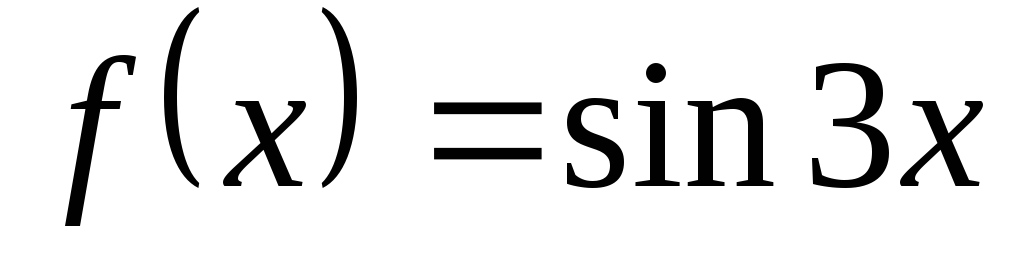. Найти,,.

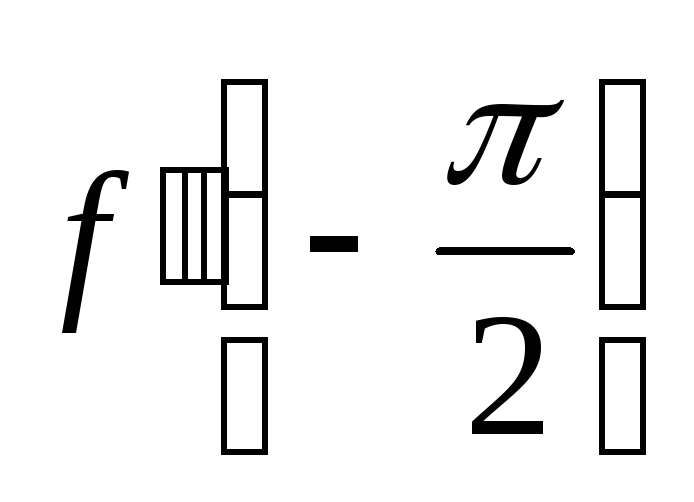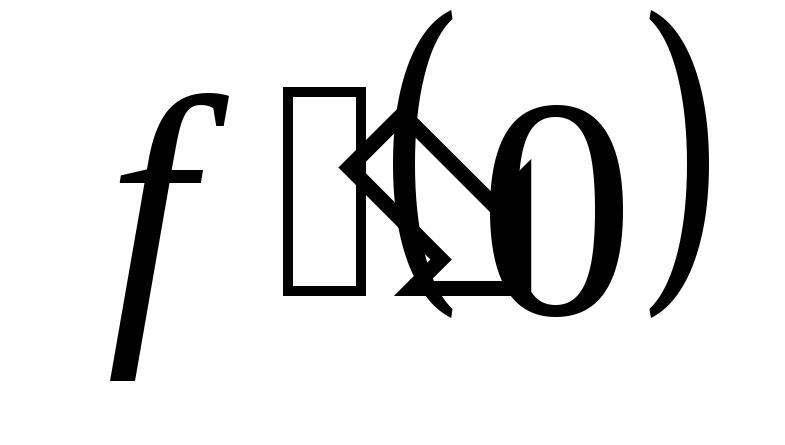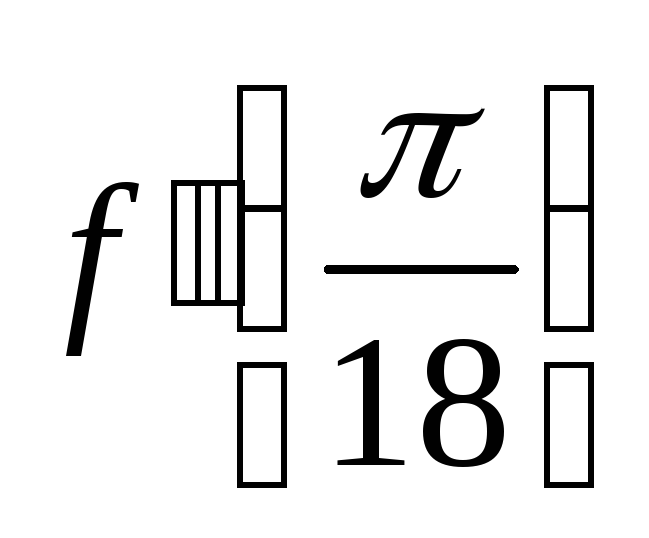3. Найти производные третьего порядка:

1) ; 2); 3).

4. Найти дифференциалы первого и второго порядков функции .

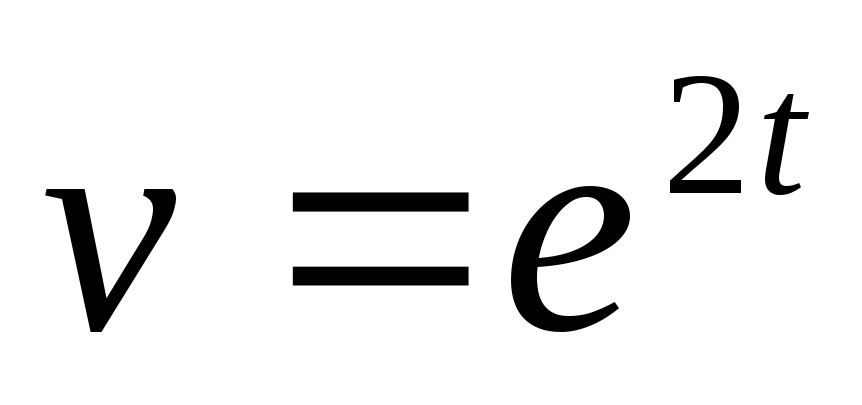5. Найти дифференциалы первого, второго и третьего порядков функций:

1) ; 2);

3) .

6. Показать, что функция 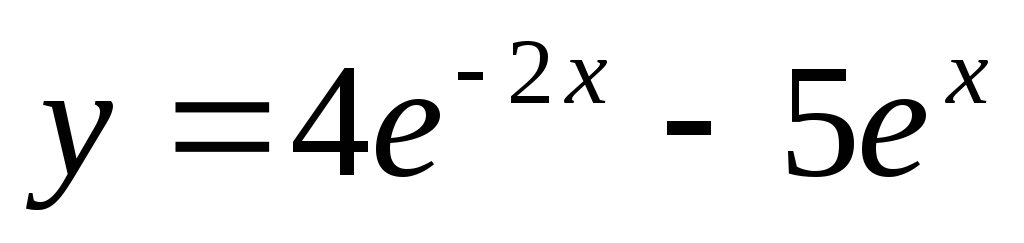удовлетворяет уравнению.

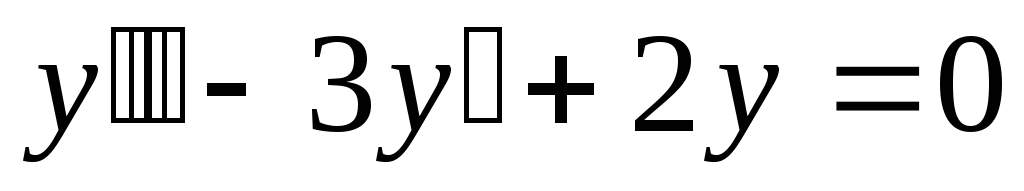Вопросы для самоконтроля:

1. Что называется производной второго порядка?

2. Что называется производной n – гопорядка?

3. Что называется дифференциалом функции?

4. Что называется дифференциалом второго порядка?

5. Что называется дифференциалом n – гопорядка? По какой формуле он вычисляется?